
Практическое занятие 5. Произведения векторов
..pdf
Практическое занятие 5. Скалярное , векторное и смешанное произведения векторов.
Упражнение 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)Что можно сказать о ненулевых векторах, если 1) a b |
0, |
2) a b |
0 |
|
|
3) a b |
0 ; |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Что можно сказать о не нулевых векторах, если a |
b |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3) Что можно сказать о не нулевых векторах, если1) |
|
|
|
|
0, 2) |
|
|
|
0, 3) |
|
|
|
|
0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
abc |
abc |
abc |
|||||||||||||||||||||||||||||
Упражнение 2. Вычислить скалярное произведение векторов a |
|
|
|
|
3;3; 2 . |
||||||||||||||||||||||||||
|
1; 3;3 ,b |
||||||||||||||||||||||||||||||
Упражнение 3. Даны точки M1 1; 3;2 |
, M2 |
3;1; 1 , M3 1; |
1;0 |
|
. Вычислить координаты |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
векторов: 1) M1M3 M2 M3 M1M2 , 2) |
M1M 2 |
M 2M3 M1M3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Упражнение 4. Используя скалярное произведение, вычислить:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) проекцию вектора i |
j |
|
|
на вектор i |
|
|
j ; |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) угол между векторами |
|
2i |
|
|
|
3 j |
5k И |
|
i |
3k |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Упражнение 5. Пусть задан вектор силы F |
2;3; |
5 .Определить величину усилия от действия |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
силы F в заданных направлениях : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
a 1; 2;3 |
|
|
|
|
|
|
|
|
|
|
|
3) c 3; |
2;0 |
||||||||||||||||
1) |
2) |
|
b (2; |
1; 1) |
|
|
|
|
|
|||||||||||||||||||||
|
Пусть даны два вектора a 1; |
2;3 |
|
|
|
|
||||||||||||||||||||||||
Упражнение 6. |
, b (2; |
1; 1) требуется вычислить |
||||||||||||||||||||||||||||
1) a a b b , 2) a b a b .
Упражнение 7. Найти координаты единичного вектора, образующего равные углы с
осями координат.
Упражнение 8. |
Какие углы образует вектор c |
3; 2;0 с осями координат. |
|||
|
|
|
|
|
|
Упражнение 9. |
Постоянная сила F 3; 2; |
1 приложена к телу и перемещает его вдоль отрезка |
|||
прямой из точки M1 1; 2;5 в точку M2 |
3;1; 2 |
. Вычислить работу силы. |
|||
Векторное произведение векторов.
Упражнение 10. Вычислить определители:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 2 |
|
i |
|
j |
k |
|
|
i |
|
j |
k |
|||
1) |
3 |
4 1 |
2) |
1 |
0 |
1 |
|
3) |
1 |
0 |
|
1 |
||||
|
3 |
2 5 |
|
0 |
1 |
3 |
|
|
|
1 1 |
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
Упражнение 11. Для векторов a 1;1;3 ,b |
2;1;2 , c 2;0;5 вычислить векторные |
||||||||||
произведения: |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1) a b; 2) a с; 3) с b; 4) a b c ; 5) a b |
a b c |
||||||||||
Упражнение 12. Вычислить площадь |
ABC , где: |
|
|
|
|||||||
1)A 2; 3;1 ; B 0;3;1 ;C 1; 3;2
2)A 0; 3;0 ; B 2;3; 1 ;C 1;0;2
Упражнение 13. ВЫЧИСЛИТЬ МОМЕНТ СИЛЫ F , ПРИЛОЖЕННОЙ В ТОЧКЕ B , ОТНОСИТЕЛЬНО
ТОЧКИ A
|
|
|
|
|
|
|
|
1) |
F |
(1; |
3; |
5), A 1; 5; 7 |
, B 3; 7; 9 ; |
||
|
|
|
|
|
|
|
|
2) |
|
F |
(2; |
4; |
1), A 1; 3; 0 |
, B 0; 3; 5 ; |
|
Упражнение 14. |
Найти все единичные вектора перпендикулярные векторам a 1; |
2;3 |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b (2; 1; 1) . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Упражнение 15. |
Найти все векторы перпендикулярные векторам a 1; 2;3 , b (2; |
1; |
1) |
||||||||
Смешанное произведение векторов. |
|
|
|||||||||
|
|
|
|
|
|
|
|||||
Упражнение 16. |
Для векторов a 1;1;3 ,b 2;1;2 , c 2;0;5 вычислить смешанное |
|
|||||||||
произведение |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
abc . |
|
|
|||||||||
Упражнение 17. Вычислить объём пирамиды, если известны координаты её вершин
1) A 2;1;4 , B 1;2;3 ,C 6;0;2 , D 3;3;3 ;2) A 2;1;5 , B 5;0;3 ,C 4;0;8 , D 6; 2;6
Упражнение 18. Проверить являются ли векторы компланарными:
a 1;2;3 ,b 1;3;0 , c 0;5;3
Упражнение 19. Лежат ли точки A 1;2; 1 , B 3;3; 4 ,C 2;2;1 ; D 5;3;0 в одной и той же плоскости ?
Упражнение 20. Три вершины тетраэдра расположены в точках
M1 1;1; 1 , M2 2;0; 1 , M3 3; 2;1 . Найти координаты четвёртой вершины D,лежащей на оси OX ,если объём тетраэдра равен 4ед 3 .
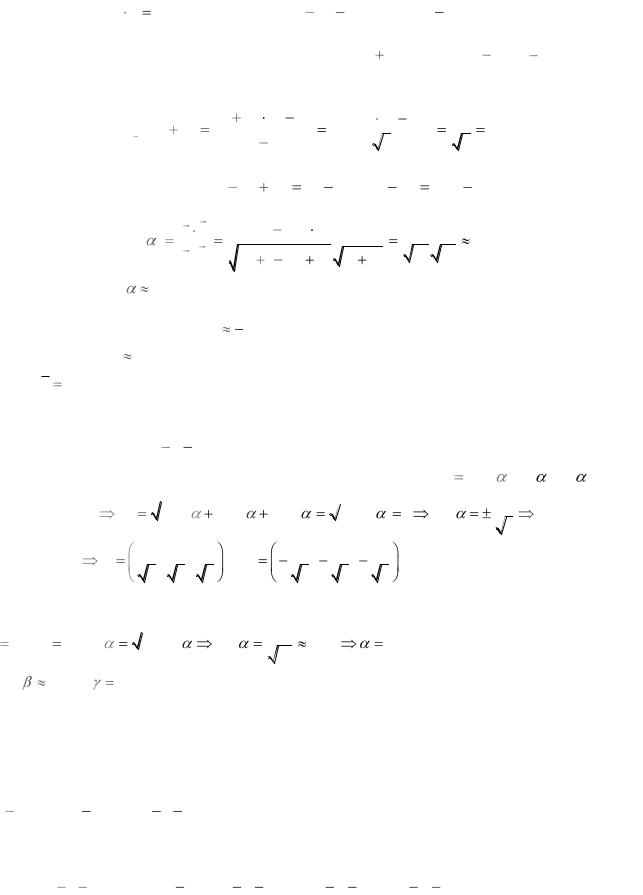
Ответы и решения. Скалярное умножение векторов.
Упражнение 2. |
|
|
|
|
|
|
|
0 ; Упражнение 3. |
1) |
|
12; 24;18 , 2) |
0; |
30;30 . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a b |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Упражнение 4. |
Решение. |
1) |
|
Сначала вычисляем векторы i |
|
|
|
|
|
j |
= |
|
1;1;0 , |
|
i |
|
j =(1; 1;0 ). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Затем по формуле |
проекцию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
i j |
|
|
|
1;1; 0 |
|
|
|
1; |
1; 0 |
|
|
0 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
ПР( |
|
|
|
|
) |
|
i |
j |
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
затем |
||||||||||||||||||||||||||||||
2) Сначала вычисляем векторы 2i |
|
3 j |
5k |
(2; |
3;5), |
|
|
|
i |
|
|
|
|
3k |
1;0; |
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
cos |
|
|
|
|
a b |
2; |
3;5 |
1; 0;3 |
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
0.9 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
22 |
|
|
3 2 |
52 |
12 |
|
32 |
|
|
|
|
|
|
|
38 |
|
|
10 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
260 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Упражнение 5. |
Решение. 1) |
|
|
|
|
|
0.9 . Усилие направлено противоположно направлению |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ПРa F |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вектора a . 2) ПРa F |
0.13 . |
направление усилия и направление вектора a совпадают. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) ПРa F 0 . Сила перпендикулярна направлению и поэтому никакого усилия в направлении вектора a нет.
Упражнение 6. Ответ.1) 3; 3; 3 , 2) (3,-3,3). Упражнение 7.Решение. Единичный вектор,
образующий равные углы с осями координат вычисляем по формуле : e cos ;cos ;cos .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
cos2 |
|
|
|
cos2 |
cos2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
e |
|
e |
|
|
|
|
|
|
|
3 |
cos |
|
|
1 cos |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||||||||||
Длина e равна |
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
e |
|
; |
; |
|
и e |
|
; |
; |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
3 |
3 |
|
3 |
2 |
3 |
|
|
3 |
|
|
3 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Упражнение 8. Указание. Каждая координата это проекция вектора на соответствующую ось.
|
|
|
|
|
|
|
|
|
|
3 |
|
|
340 . Аналогично определяются |
|
3 ПР |
|
c |
|
c |
cos |
13 cos |
cos |
|
0.83 |
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||
|
|
|
||||||||||||
|
i |
|
|
|
|
|
|
|
13 |
|
|
|
||
углы |
1240 и |
900 . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
Упражнение 9. Ответ. А=3.
Векторное умножение векторов.
Упражнение 10. Определители вычисляем разложением по первой строке:
1) 50; 2) 1; 3;1 ; 3) 1; 1;1 .
Упражнение 11. Векторные произведения вычисляем по формуле
1) ( 1; 8;3), 2) (5;1; 2), 3) ( 5; 14; 2), 4) ( 6; 9;5),5) ( 2, 3, 6)

Упражнение 12. 1). Площадь вычисляем согласно формуле ,с учётом, что площадь треугольника в два раза меньше площади параллелограмма.
1 шаг. Вычисляем по формуле (4.14) векторное произведение, a b , где
a AB 2;6; 1 ;
b AC 1;0;1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
2 |
|
6 |
|
1 |
|
6; 1; 6 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
шаг. Находим длину векторного произведения |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
62 |
1 2 |
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
|
73 |
|
8.5 . |
Площадь треугольника |
ABC численно |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равна половине |
длины векторного произведения S |
|
a b |
|
|
|
8.5 |
4.25 (ед. 2 ). |
||||||||||||||||||||||
ABC |
2 |
|
|
|
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2).Решая аналогично, получаем S |
|
ABC |
|
|
|
7.9 (ед. 2 ). |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Упражнение 13. Указание. Используйте формулу вычисления момента силы.
Упражнение 14. Решение. Находим вектор c перпендикулярный заданным векторам
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
8.4 . |
|
a , b c |
a |
b |
1 |
2 |
3 |
|
5; 6;3 |
. Вычисляем длину вектора c . |
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Единичный вектор e перпендикулярный векторам a , b равен e |
|
0.6; 0.7; 0.4 . |
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
c |
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Вектор e1 |
|
e также перпендикулярен данным векторам a , b . |
|
|
|
|
|
|
||||||||||||||||||||
|
|
e и e1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ответ. |
Векторы |
перпендикулярны векторам a , b . |
|
|
|
|
|
|
||||||||||||||||||||
Упражнение 15. Все данные вектора |
коллинеарны вектору c из упражнения 13. |
|||||||||||||||||||||||||||
Ответом является вектор 5t;6t;3t , где t произвольный параметр.
Смешанное произведение векторов.
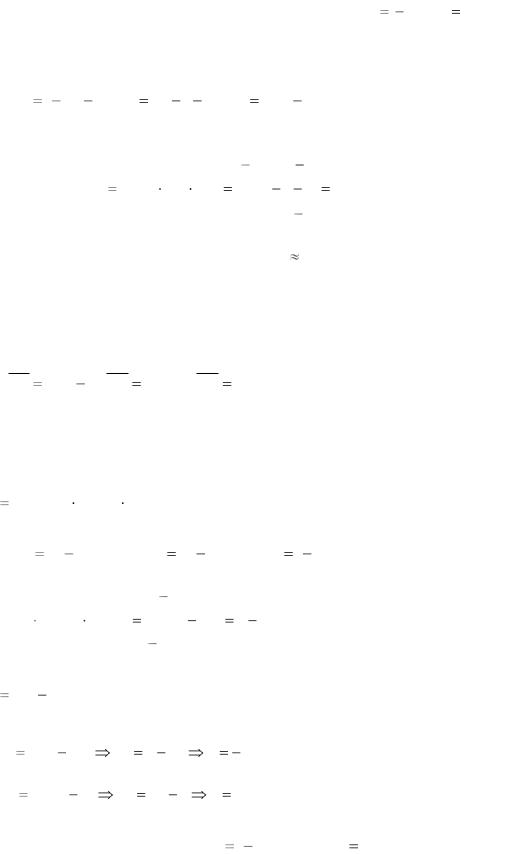
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
3 |
|
Упражнение 16. |
Произведение вычисляем по формуле |
|
|
|
2 |
1 |
2 |
17 |
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
abc |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 5 |
|
|
Упражнение 17. |
Решаем задачу 1). Согласно формуле вычисляем векторы |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
AB |
1;1; |
1 , AC |
|
4; 1; 2 , AD |
|
1; 2; |
1 . |
Объём пирамиды равен |
|||||||||||||||||||
смешанному произведению |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
V |
|
AB AC AD |
|
|
4 |
1 |
2 |
|
12 |
|
|
|
|
|
|
|
|||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решаем задачу 2) аналогичным образом V |
2.3. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
Упражнение 18. Указание. Проверьте чему равно смешанное произведение.
Ответ. Да, являются.
Упражнение 19. Для этого нужно проверить компланарность векторов
AB 2;1; 3 ; AC 1;0; 2 ; AC 4;1;1 .
Ответ. Не лежат.
Упражнение 20. Согласно формуле объём пирамиды равен
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
v |
|
|
|
M |
2 M4 |
M2 M3 M2 M1 |
|
. Вычисляем координаты векторов |
|||||||||||||||||||||||
|
6 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
M2M4 |
x 2;0;1 , M2M3 |
1; |
3; 2 |
, M2M1 |
1;1;0 |
. Отсюда |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
0 1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2x . Выписываем формулу объёма |
||||||||||||
|
M 2 M 4 M 2 M3 |
M 2 M1 |
1 |
|
|
3 2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 0 |
|
|
|
|
|
|
v |
1 |
|
|
|
|
|
2x |
|
. Решая это уравнение получаем координаты вершины M 4 |
||||||||||||||||||||||
|
|
2 |
|
|
|||||||||||||||||||||||||||
6 |
|
|
|||||||||||||||||||||||||||||
1) 4 |
|
1 |
|
2 |
|
|
2x |
24 |
2 |
|
|
2x |
x |
11; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) 4 |
|
1 |
2x |
2 |
24 |
2x |
2 |
x |
13; |
|
|
||||||||||||||||||||
6 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: Возможны две ситуации 1)M4 |
|
11;0;0 ; 2)M4 |
13;0;0 |
||||||||||||||||||||||||||||
