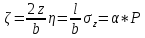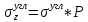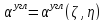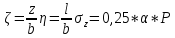Задача Буссинеска

Задача от действия силы N сосредоточенной силы на линейно деформируемое полупространство. Буссинеск создал модель линейно деформируемого полупространства. Её свойства:

- линейно деформируема

- однородно (свойства в каждой точке грунтового массива одинаковы)

- изотропно (по любому направлению свойства одинаковы)

Рис 7.4

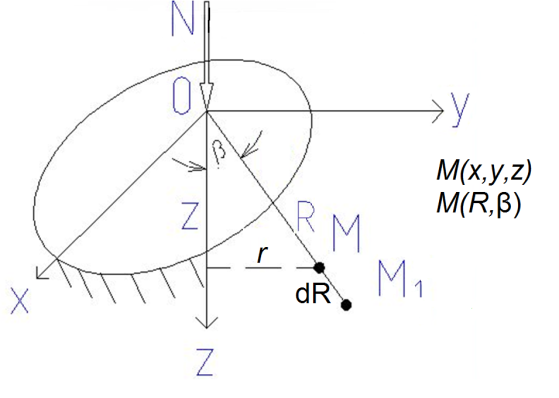
От действия силы N во всех точках полупространства возникает сложное напряженное состояние. В каждой точке полупространства, удаленной от точки О будет действовать шесть составляющих: σ_х, σ_у, σ_z, τ_xy, τ_xy, τ_xy.

Под действием силы N точка М переместится в направлении радиуса R на величину s. Чем дальше от точки О будет расположена точка М, тем меньше будет ее перемещение и при R=∞ перемещение будет равно 0. Следовательно s можно принять обратно пропорционально R:

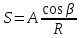
А – коэффициент пропорциональности.

При одном и том же значении R для разных значений угла β перемещение точек будут не одинаковы: наибольшее перемещение получит точка расположенная на оси z, то есть при β=0. С увеличением β перемещение по направлению радиуса R уменьшаются и при β=90° (на поверхности грунта) будут равны 0.

Рассмотрим точку М₁на продолжении радиуса R. Пусть она находится на расстоянии dR.

S₁<S

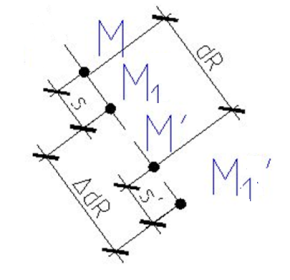
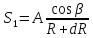
Относительная деформация грунта на отрезке dR составляет:

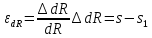
Пренебрегая величиной RdR, малой по сравнению с R²и, учитывая линейную зависимость между напряжениями и деформациями, найдем выражение для напряжений сжатия, действующих на площадке перпендикулярной направлению R:

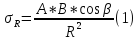
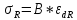
В – коэффициент пропорциональности между σ_Rи ε_dR.

Лекция 8 – 18.11.11

Для нахождения произведения коэффициентов А и В отсечем мысленно часть полупространства полушаровой поверхности, имеющей центр в точке 0 и радиус r и составим уравнение равновесия проекцией на ось z всех сил, действующих на отсеченный элемент для невесомой среды.

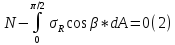
dА – площадь кольца полушоровой поверхности при изменении угла β на величину dβ.

Рис 8.1

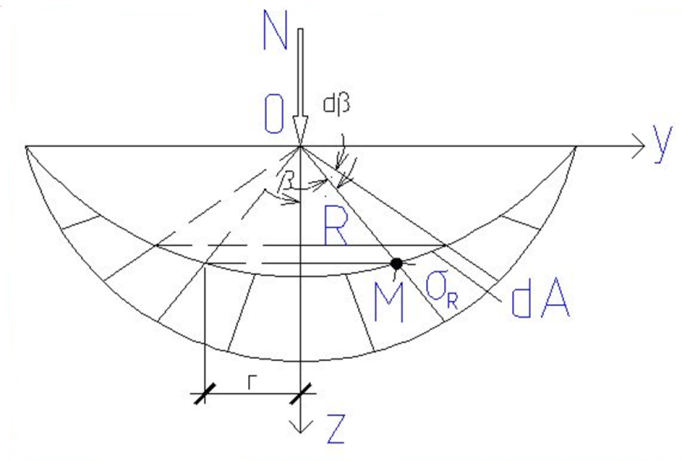
Подставив в уравнение (2) значение σ_R, определенное по выражению (1) и решив его, найдем произведение АВ:

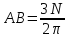
Подставим его в (1):

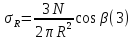
Напряжение σ_Rдействует на наклонную площадку dА. Рассматривая равновесие элементарной треугольной призмы, составим уравнение проекции всех сил на вертикальную ось.

Рис 8.2

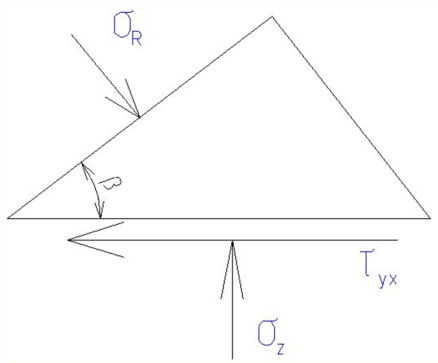
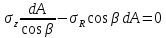
Подставив выражение σ_Rиз (3), найдем вертикальное напряжение, которое принимается с положительным знаком при сжатии:

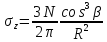
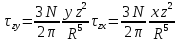
Так как , =>

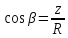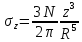
Учитывая, что R² = r²+z²

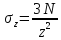
Где

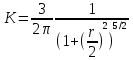
Аналогично могут быть найдены остальные компоненты напр-ий.

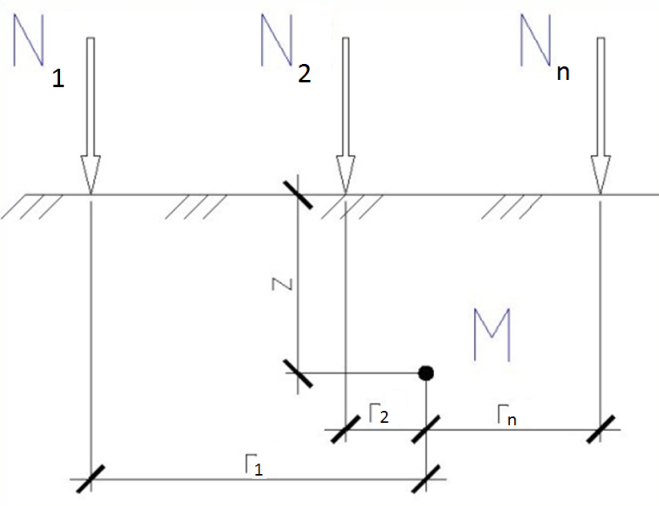
Действие нескольких сосредоточенных сил

Если к поверхности изотропного однородного линейно-деформируемого полупространства, приложено несколько сил N₁, N₂, … N_z, то при прямой пропорциональности между напряжениями и деформациями можно использоватьметод суперпозиции(принцип независимости действия сил).

Этот принцип дает возможность подсчитывать результат воздействия на грунтовое основание системы сил, сложением каждой силы в отдельности и найти значение σ_R, в любой (.) М простым суммированием:

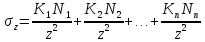
Рис 8.3

Действие местного равномерного распределенного давления

Задача Лява

Рис 8.4

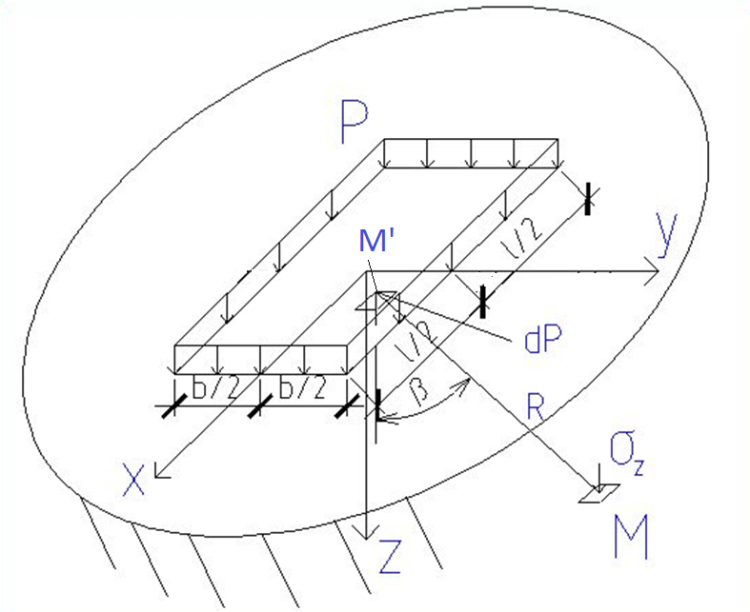
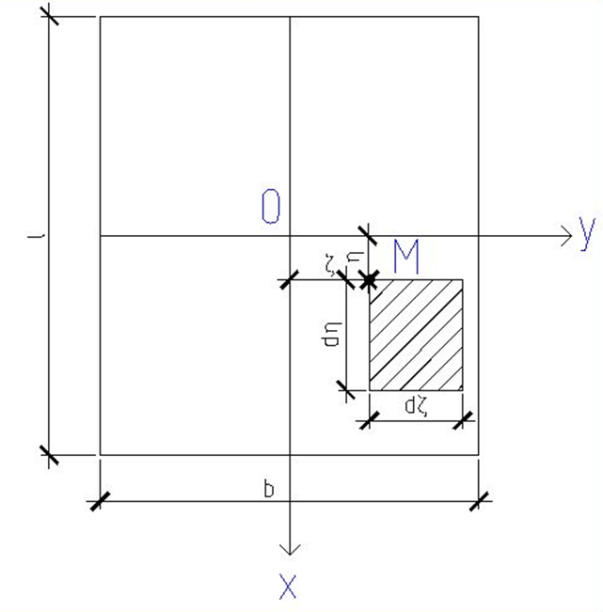
Выделим бесконечно малый элемент загруженной площадки и считая нагрузку на этот элемент сосредоточенной (для точек расположенных под прямоугольной площадью загружения). Пользуясь формулами Бусенеска определяем составляющие нагружения.

Проинтегрировать полученные выражения в пределах всей площади можно получить формулы для составляющих напряжений от действия данной нагрузки.

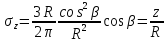
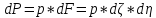
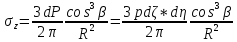
На множество площадок:

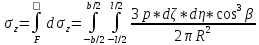
Для точек, принадлежащих центральной и угловой вертикали:

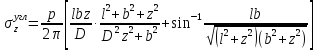
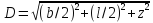
Лям составил таблицы для точек принадлежащих центральной и угловой вертикалям:

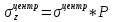
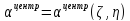
Функция безразмерных координат ζ и η: