- •Расчет монолитной железобетонной плиты
- •Расчет плиты по прочности.
- •1.2 Расчет плиты по второй группе предельных состояний
- •1.2.1 Расчёт по образованию трещин
- •Расчёт ширины раскрытия трещин
- •1.2.3 Расчёт плиты по прогибам
- •Расчет сборного ригеля поперечной рамы
- •2.1 Расчет ригеля по прочности.
- •2.2.1 Расчётные нагрузки
- •2.2.2 Расчётные пролёты ригеля
- •2.2.3 Расчетные изгибающие моменты (рис. 9)
- •2.2.4 Расчетные поперечные силы (рис. 9)
- •Расчет ригеля на прочность по нормальным сечениям
- •Определение площади поперечного сечения поперечной арматуры на отрыв
- •Расчет крайнего ригеля на прочность по наклонным сечениям на действие поперечных сил
- •2.2.8 Определение длины приопорных участков крайнего ригеля
- •2.2.9 Обрыв продольной арматуры в крайнем ригеле. Построение эпюры несущей способности ригеля
1.2.3 Расчёт плиты по прогибам
Полная кривизна для участков с трещинами в растянутой зоне определяется по формуле 7.3.8 [4]:
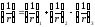 ,
а полный прогиб плиты:
,
а полный прогиб плиты:
 где:
где:
 - кривизна от
продолжительного действия постоянной
и длительной нагрузки
- кривизна от
продолжительного действия постоянной
и длительной нагрузки
Из расчёта acrc1: Ebred =Eb1= 5000МПа, αs2 = 40, xm = 134,85 мм.


Момент инерции приведённого сечения без учёта растянутого бетона:
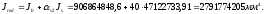

где:
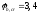 - коэффициент ползучести бетона.
- коэффициент ползучести бетона.
Принято:
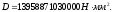
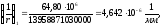

Кривизна от непродолжительного действия всей нагрузки:
 ,
где Мn
= 78,45 кН∙м
,
где Мn
= 78,45 кН∙м
Из расчёта acrc2: Ebred =Eb1= 7333 МПа, αs2 = 27,27, xm = 110,91 мм.

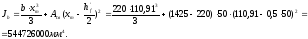




Кривизна от непродолжительного действия постоянной и длительной нагрузки:
 ,
где Mnl
= 64,80 кН∙м
,
где Mnl
= 64,80 кН∙м
Из расчёта acrc2, (так как нагрузка носит непродолжительный характер): Ebred =Eb1= 7333 МПа, αs2 = 27,27, xm = 110,91 мм,
 .
.
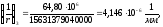


Плита удовлетворяет требованиям таблицы 19 [2]:
а) эстетико-психологическим

б) конструктивным

Вывод: плита удовлетворяет требованиям по второй группе предельных состояний.
Расчет сборного ригеля поперечной рамы
Для сборного
железобетонного перекрытия требуется
рассчитать сборный ригель, используя
данные и результаты расчёта плиты. Сетка
колонн .
Для ригеля крайнего пролета необходимо
построить эпюры моментов от нагрузки
и его несущей способности.
.
Для ригеля крайнего пролета необходимо
построить эпюры моментов от нагрузки
и его несущей способности.
Данные для расчёта:
бетон тяжелый, класс бетона B15,
коэффициент работы бетона .
Расчётные сопротивления бетона с учетом
.
Расчётные сопротивления бетона с учетом равны:
равны:
 .
Продольная и поперечная арматура –
класса A400.
Коэффициент снижения временной нагрузки
.
Продольная и поперечная арматура –
класса A400.
Коэффициент снижения временной нагрузки

Армирование ригеля представлено двумя продольными каркасами и двухрядным расположением стержней (рис. 8).

Рис. 8 – Поперечное сечение ригеля
2.1 Расчет ригеля по прочности.
2.2.1 Расчётные нагрузки
Нагрузка на ригель
собирается с грузовой полосы (представленной
на рис. 9)
шириной ,
равной расстоянию между осями ригелей
(по
,
равной расстоянию между осями ригелей
(по с
каждой стороны от оси ригеля).
с
каждой стороны от оси ригеля).
а) постоянная
нагрузка (с
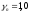 и
и ):
):
вес железобетонных плит с заливкой швов
 принят
по данным типовой серии ИИ 24-1 данных
плит:
принят
по данным типовой серии ИИ 24-1 данных
плит:
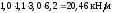 ;
;
вес пола и перегородок:
 ;
;
собственный вес
ригеля с приведённой шириной
 и высотой
и высотой (размеры предварительные):
(размеры предварительные):
 ;
;
Итого постоянная
нагрузка .
.
б) временная
нагрузка с
коэффициентом снижения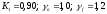 :
:
 .
.
Полная расчетная нагрузка:
 .
.
2.2.2 Расчётные пролёты ригеля
При поперечном
сечении колонн
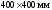 (
( )
и вылете консолей
)
и вылете консолей расчётные пролёты ригеля равны (рис.9):
расчётные пролёты ригеля равны (рис.9):
крайний пролет:
 ;
;средний пролет:
 .
.
2.2.3 Расчетные изгибающие моменты (рис. 9)
В крайнем пролете:
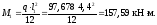
На крайней опоре:
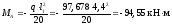
В средних пролетах и на средних опорах:
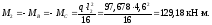
Отрицательные
моменты в пролетах при
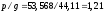 (табл.
1 и рис. 9 [10]):
(табл.
1 и рис. 9 [10]):
в крайнем пролёте
для точки «4» при
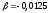
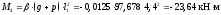 ;
;
в среднем пролёте
для точки «6» при

 .
.
2.2.4 Расчетные поперечные силы (рис. 9)
Поперечная сила в каждом пролёте определяется как для простой балки с опорными моментами на концах.
На крайней опоре:
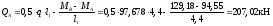
На опоре B слева:

На опоре
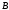 справа
и на средних опорах:
справа
и на средних опорах:
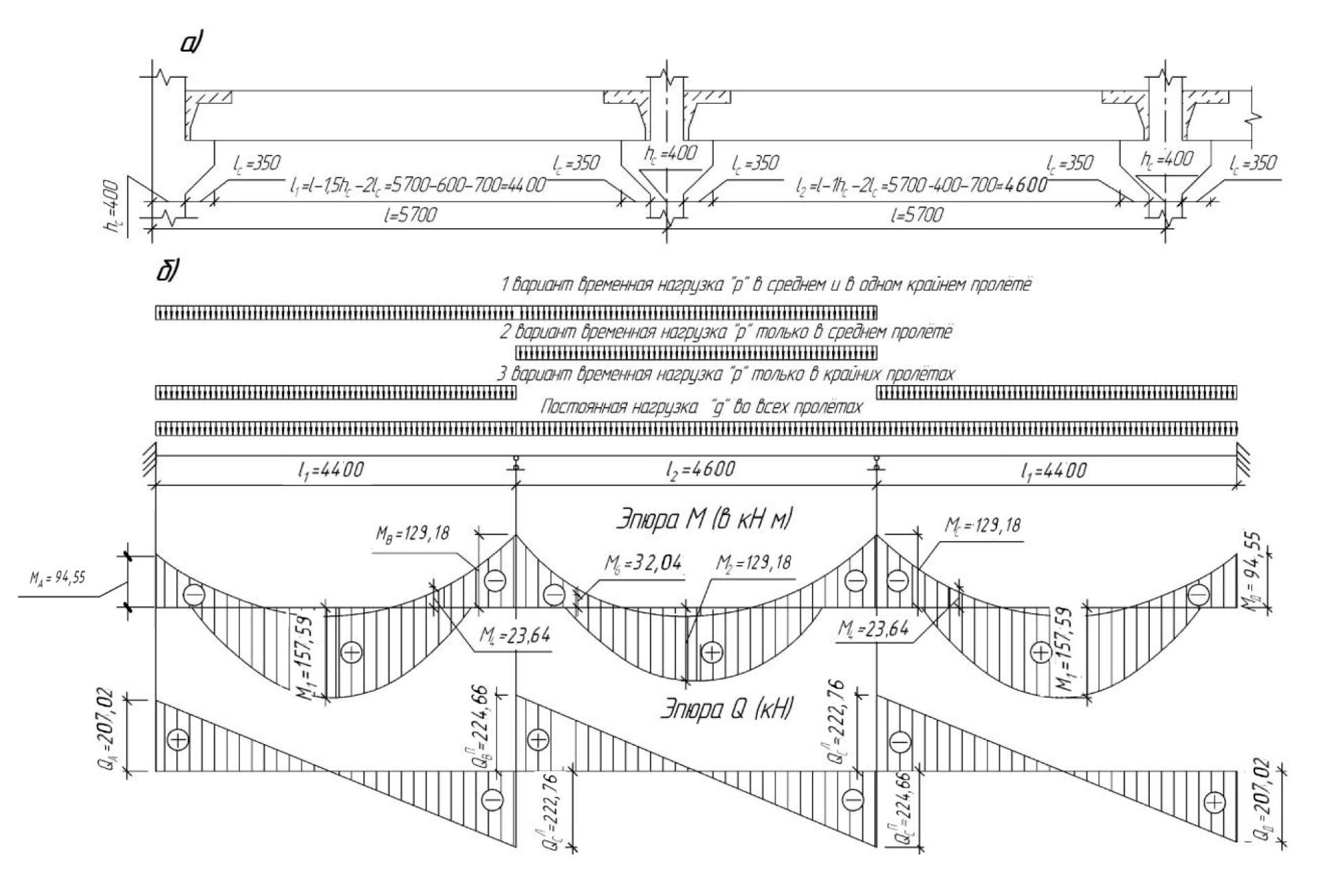
Рисунок 9 – К расчету многопролетного ригеля
Расчет ригеля на прочность по нормальным сечениям
Для арматуры класса
A400
 .
Ширина сечения ригеля
.
Ширина сечения ригеля .
Высота ригеля определяется по моменту
в крайнем пролёте
.
Высота ригеля определяется по моменту
в крайнем пролёте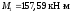 ,
задаваясь значением
,
задаваясь значением .
Откуда
.
Откуда .
Сечение рассчитывается как прямоугольное
по формуле (1) [10]:
.
Сечение рассчитывается как прямоугольное
по формуле (1) [10]:

 ;
;
принимаем
 (
(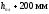 ).
).
Расчет арматуры
Расчетное
сопротивление арматуры класса А400
 (приложение
В [10]).
(приложение
В [10]).
а) Крайний пролёт.
 (предварительно),
тогда
(предварительно),
тогда
 (арматура
расположена в два ряда по высоте).
(арматура
расположена в два ряда по высоте).

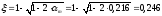
Аs=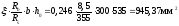
Принято .
.
 (где
30мм - толщина закладной детали, к которой
привариваются продольные стержни; 20
диаметр арматуры 18 по рифам, 50 – расстояние
между стержнями диаметром 18 мм), пересчёт
а
не требуется.
(где
30мм - толщина закладной детали, к которой
привариваются продольные стержни; 20
диаметр арматуры 18 по рифам, 50 – расстояние
между стержнями диаметром 18 мм), пересчёт
а
не требуется.
Проверка
условия
 ,
необходима при расчёте статически
неопределимых конструкций по методу
предельного равновесия.
,
необходима при расчёте статически
неопределимых конструкций по методу
предельного равновесия.
б) Крайняя опора.
 (предварительно),
тогда
(предварительно),
тогда
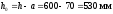 (арматура расположена в один ряд по
высоте).
(арматура расположена в один ряд по
высоте).

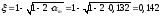

Принято
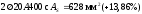 .
.
В этом случае
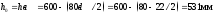 (где 80мм - расстояние от верха ригеля до
низа арматурного стержня), что соответствует
предварительно принятому.
(где 80мм - расстояние от верха ригеля до
низа арматурного стержня), что соответствует
предварительно принятому.
в) Верхняя пролетная арматура крайнего пролета по моменту в сечении «4»
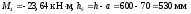 (арматура расположена
в один ряд по высоте).
(арматура расположена
в один ряд по высоте).

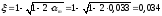
Аs=
Принято
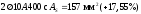 .
.
При
стыковом соединении стержней должно
выполняться
условие

Принимаем:

г) Средний пролет.
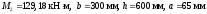 (предварительно),
тогда
(предварительно),
тогда
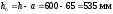 (арматура расположена в два ряда по
высоте).
(арматура расположена в два ряда по
высоте).

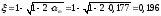
Аs=
Принято
 .
.
 ,
пересчет а
не требуется.
,
пересчет а
не требуется.
д) Средняя опора.

 (предварительно),
тогда
(предварительно),
тогда
 (арматура расположена в один ряд по
высоте).
(арматура расположена в один ряд по
высоте).



Принято
 .
.
В этом случае
 ,
что соответствует предварительно
принятому.
,
что соответствует предварительно
принятому.
е) Верхняя пролётная арматура среднего пролета по моменту в сечении «6»
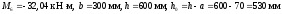 (арматура расположена
в один ряд по высоте).
(арматура расположена
в один ряд по высоте).



Принято