
- •1. Начертательная геометрия. Определение.
- •2. Параметризация
- •Количественные
- •Качественные
- •Параметры формы
- •4. Ортогональное проецирование
- •5. Косоугольное проецирование
- •8. Инварианты проецирования
- •9. Кривая
- •11. Линейчатые поверхности
- •12. Способы образования конечностей
- •13. Позиционные задачи
- •14. Построение перпендикулярной и параллельной прямой и плоскости относительно плоскости общего положения.
- •15. Сущность метода качающейся плоскости и плоскостей уровня для решения позиционных задач.
- •16. Частные случаи пересечения поверхностей второго порядка
- •17. Метод преобразования проекций.
- •18. Метрическими называются задачи
- •19.Развертки точные, приближенные и условные.
- •20.Проекции с числовыми отметками
- •21. Задание плоскости и отрезка в плоскости с числовыми отметками.
- •23. Аксонометрические проекции. Определение. Понятие точной и приведенной аксонометрии.
- •24. Изоиметрия. Диметрия. Триметрия
- •Изометрические проекции
- •Диметрические проекции
- •Прямоугольная диметрическая проекция
- •Триметрические проекции
- •25. Перспектива. Метод архитекторов
Начертательная Геометрия
1. Начертательная геометрия. Определение.
Начертательная геометрия является разделом геометрии, в котором изучаются методы изображения пространственных фигур на чертеже и алгоритмы решения позиционных, метрических и конструктивных задач.
Позиционные задачи- задачи на взаимную принадлежность и пересечение фигур.
Метрические задачи-задачи на определение расстояний и натуральных величин геометрических фигур.
Конструктивные задачи- задачи на построение геометрических фигур, отвечающих заданным условиям.
Значение: учит грамотно владеть языком чертежа, создавать чертежи и свободно читать их.
2. Параметризация
Параметризация– присвоение объекту, который принадлежит определенному множеству, свойств, которые будет выделять его из этого множества.
Основные понятия:
Система координат
Возможностью задания параметров в различных системах координат (прямоугольной, полярной или смешанной) является проблемой параметризации, так как это существенно увеличивает количество вариантов задания параметров.
Идеальная система параметризации должна выявлять все используемые соотношения, формализовать их и включать в параметрическую модель (это можно не говорить, наверное)
Параметры – независимые друг от друга обозначения, которые позволяют выделить объект из подобных
ПАРАМЕТРЫ


(линейные, угловые
и т.п)
Их можно измерить
(Параллельность,
касание, симметрия и т.п)
Измерять не нужно
Количественные
Качественные


Параметры положения
(зависят от относительно системы
координат)
(не зависят от
относительной системы координат)
Параметры формы
3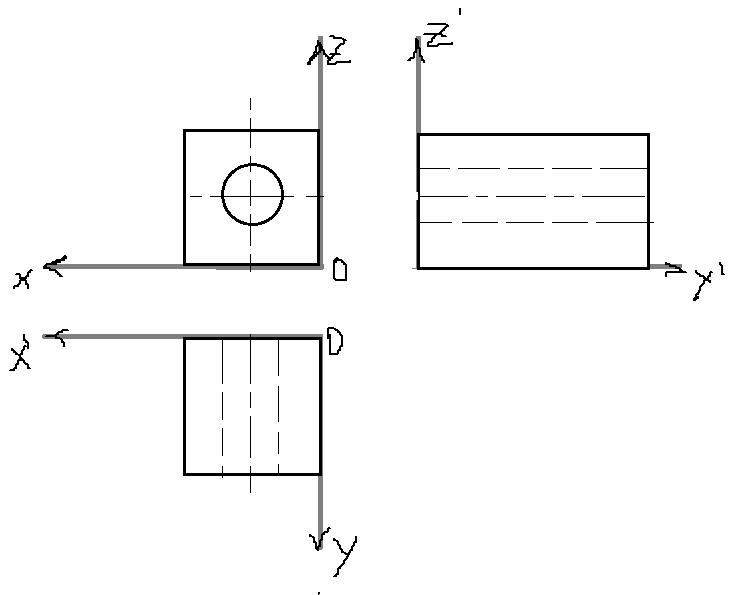 .
Эпюр Монжа. Технический чертежТехнический
чертеж является разверткой куба
на грани которого перенесено изображение
трехмерного объекта.
.
Эпюр Монжа. Технический чертежТехнический
чертеж является разверткой куба
на грани которого перенесено изображение
трехмерного объекта.
Технический чертеж является системой внутренней параметризации
Эпюр Монжа(ортогональный чертеж, комплексный чертеж) - декартова система координат, состоящая из трех взаимно перпендикулярных плоскостей, линии пересечения которых образуют оси координат.
П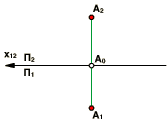 рямая
А1 А0 совпадет с продолжением прямой А2
А0, и мы получаем прямую А1 А2, которая
будет оси проекций П2 /П1. Эта прямая
называется линией проекционной связи
или простолинией связи.
рямая
А1 А0 совпадет с продолжением прямой А2
А0, и мы получаем прямую А1 А2, которая
будет оси проекций П2 /П1. Эта прямая
называется линией проекционной связи
или простолинией связи.
Линия связи- это прямая, связывающая пары проекций одной и той же точки, и перпендикулярная оси проекций.
Утверждение: Две прямоугольные проекции точки полностью А определяют её положение в пространстве основных плоскостей проекций.
4. Ортогональное проецирование
при параллельном проецировании проецирующие лучи параллельны между собой.
Ортогональное проецирование- это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
Свойства параллельного проецирования + свойства ортог. проец-ия
Свойства параллельного проецирования: (первые 6 от центрального входят сюда!)
Проекцией точки является точка.
Проекцией линии является линия.
П
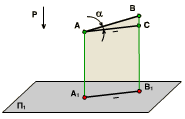 роекцией
прямой в общем случае является прямая.
(Если прямая совпадает с проецирующим
лучом, то её проекцией является точка).
роекцией
прямой в общем случае является прямая.
(Если прямая совпадает с проецирующим
лучом, то её проекцией является точка).Если точка принадлежит линии, то проекция точки принадлежит проекции линии.
Точка пересечения линий проецируется в точку пересечения проекций этих линий.
В общем случае плоский многогранник проецируется в многогранник с тем же числом вершин.
Проекции параллельных прямых параллельны.
Е
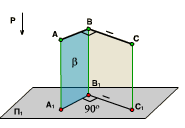 сли
точка делит длину отрезка в отношении
m:n, то проекция этой точки делит длину
проекции отрезка в том же отношении.
сли
точка делит длину отрезка в отношении
m:n, то проекция этой точки делит длину
проекции отрезка в том же отношении.Плоская фигура, параллельная плоскости проекций, проецируется без искажения
Свойства ортогонального проецирования:
Длина отрезка равна длине его проекции, делённой на косинус угла наклона отрезка к плоскости проекций.
Теорема о проецировании прямого угла: Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.
