4 Расчёт по предельным состояниям второй группы

4.1 Общие указания к расчёту

Расчёт по второму предельному состоянию конструкций, производится от расчётных нагрузок при коэффициенте надёжности по нагрузке γ_f= 1,0.

Для упрощения расчёта наиболее нагруженное фактическое поперечное сечение балки 1-1 приводится к условному расчётному (рисунок 1).

В курсовом проекте для упрощения расчёта проверяется образование и раскрытие трещин только нормальных к оси элемента.

Подсчёт потерь предварительного напряжения производится по формулам представленным в СП 52-102-2004.

Первые потери σ_sр(1)будут равны при способах натяжения:

–механическом на упоры стенда

–электротермическом на форму

Вторые потери – для всех способов одинаковы

Полные потери .

4.2 Геометрические характеристики

h_1-1= 1160 мм;h_{0 1-1}= 1075 мм;

Площадь приведённого поперечного сечения относительно нижней грани балки:

А_red=A+α·A_sp=210·200+80·765+180·195+6,67·1256=146677,5 мм²

Статический момент приведённого поперечного сечения относительно нижней грани балки:

Расстояние от нижней грани балки до центра тяжести приведённого сечения:

;

Момент инерции приведённого сечения относительно главной оси, проходящей через центр тяжести приведённого сечения перпендикулярного плоскости изгиба:

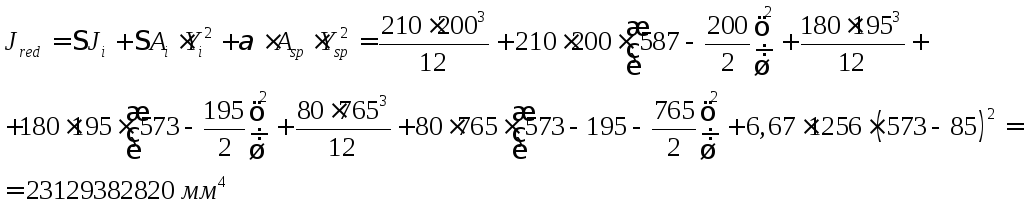
Упругий момент сопротивления приведённого сечения по растянутой зоне:

Расстояние от центра тяжести приведённого сечения до условной ядровой точки, более удалённой от крайнего растянутого волокна

4.3 Определение потерь предварительного напряжения арматуры

Потери предварительного напряжения арматуры зависят от способа её натяжения и её класса. В нашем примере принятая величина предварительного напряжения арматуры σ_sp=500 МПа.

Первые потери σ_sр(1):

1) От релаксации напряжённой арматуры

2) От температурного перепада при ∆t= 65˚C

3) От деформации анкеров натяжных устройств

где ∆l = 2,0 мм.

При натяжении на упоры стенда механическим способом с фиксацией стержней в инвентарных зажимах снаружи упоров на расстоянии 1,5 м от торцов балки длина арматуры l= 12 + 1,5·2 = 15 м.

где 12 м – номинальная длина балки.

Передаточную прочность бетона принимаем равной отпускаемой прочности, то есть R_bp=R_отп= 0,7·В_.= 0,7·25 = 17,5 МПа, что несколько больше минимально допустимой, устанавливаемой п. 2.6 (СНиП 2.03.01-84*. «Бетонные и железобетонные конструкции»). (15 МПа и 50% от принятого класса бетона).

Суммарные первые потери напряжений арматуры

Вторые потери σ_sp(2)

1) От усадки бетона σ_sp5=_b,shE_s= 0,0002200000 = 40 МПа

_b,sh= 0,0002 (для В25) – деформации усадки бетона

2) От ползучести бетона

где – коэффициент армирования

А = 210200+80765+180195 = 138300 мм²

Р₍₁₎== (500 – 137,92)1256 = 454772,5 Н – усилие обжатия бетона напряженной арматуры за вычетом первых потерь.

– напряжения обжатия в бетоне на уровне центра тяжести сечения продольной напряженной арматуры y_s = e_op= 488 мм

– коэффициент ползучести бетона

Суммарные вторые потери предварительного напряжения арматуры:

σ_sp(2)=σ_sp5+σ_sp6= 40+71,27 = 111,27 МПа

Полные потери предварительного напряжения арматуры:

σ_sp=σ_sp(1)+σ_sp(2)= 137,92 + 111,27 = 249,2 МПа, что больше установленного минимального значения потерь, равного 100 МПа.