
- •И.В. Молев основы железобетонных конструкций
- •1.1. Определение и сущность железобетона
- •1.2. Достоинства и недостатки железобетона.
- •1.3. Виды железобетонных конструкций и область их применения железобетона.
- •1.4. Краткие исторические сведения о возникновении и развитии железобетона.
- •2. Структура (строение) бетона
- •3. Усадка бетона и начальные напряжения
- •4. Прочность бетона
- •1.5. Классы и марки бетона
- •6. Деформативность бетона
- •7. Модуль деформаций бетона
- •Арматура для железобетонных конструкций
- •1. Назначение арматуры и требования к ней
- •2. Виды арматуры
- •3. Физико-механические свойства арматурных сталей
- •4. Классификация арматуры по основным характеристикам. Сортамент арматуры
- •5. Сварные арматурные изделия
- •6. Соединения арматуры
- •Основные свойства железобетона
- •1. Общие сведения
- •2. Содержание арматуры
- •3. Значение трещиностойкости
- •4. Сцепление арматуры с бетоном
- •5. Анкеровка арматуры в бетоне
- •6. Усадка бетона при наличии арматуры
- •7. Ползучесть бетона при наличии арматуры
- •8. Коррозия железобетона и меры защиты от неё
- •9. Защитный слой бетона и минимальные расстояния между стержнями
- •1. Методы расчёта железобетонных конструкций
- •2. Сущность метода расчета конструкций по предельным состояниям
- •3. Две группы предельных состояний
- •4. Расчётные факторы
- •5. Классификация нагрузок. Нормативные и расчётные нагрузки
- •6. Степень ответственности зданий и сооружений
- •7. Нормативные и расчётные сопротивления бетона
- •8. Нормативные и расчётные сопротивления арматуры
- •9. Структура расчётных формул
- •1. Три стадии напряжённо-деформированного состояния железобетонных элементов
- •2. Классификация изгибаемых элементов
- •2.2. Плиты
- •Расчет изгибаемых элементов на почность по сечениям нормальным к продольной оси элемента
- •1. Предпосылки расчёта на прочность по нормальным сечениям
- •2. Расчёт изгибаемых элементов прямоугольного сечения с одиночной арматурой
- •3. Понятие о минимальном проценте армирования
- •2. Расчёт изгибаемых элементов таврового сечения
- •2) Расчёт прочности изгибаемых элементов таврового сечения по I случаю расчёта
- •3) Расчёт прочности изгибаемых элементов таврового сечения по II случаю расчёта
- •Расчет изгибаемых элементов на почность
- •2. Расчёт изгибаемых элементов по сжатой бетонной полосе между наклонными сечениями
- •3. Расчёт изгибаемых элементов по наклонным сечениям на действие поперечных сил (расчёт поперечной арматуры)
- •4. Расчёт изгибаемых элементов по наклонным
- •5. Конструктивные требования к постановке поперечной арматуры
- •1. Классификация сжатых элементов
- •2. Основы конструирования сжатых элементов
- •3. Расчёт элементов сжатых со случайным эксцентриситетом в форме центрального сжатия
- •Расчет внецентренно сжатых элементов
- •1. О характере работы и разрушения внецентренно сжатых элементов
- •Учёт влияния прогиба элемента
- •3. Расчёт сжатых элементов прямоугольного сечения в случае больших эксцентриситетов
- •4. Расчёт сжатых элементов прямоугольного сечения в случае малых эксцентриситетов
- •1. Общие сведения и конструктивные особенности
- •2. Расчёт прочности центрально растянутых элементов
- •3. Расчёт прочности элементов прямоугольного сечения, внецентренно растянутых в плоскости симметрии
3. Понятие о минимальном проценте армирования
Для
того, чтобы несущая способность
железобетонного элемента работающего
с трещинами в растянутой зоне по стадии
разрушения была не меньше несущей
способности бетонного элемента
работающего до образования трещин
устанавливают величины минимального
процента армирования сечения
![]() в
зависимости от площади бетонного сечения
элемента
в
зависимости от площади бетонного сечения
элемента![]() ,
т.е. площадь арматуры в сечении элемента
должна быть не менее минимальной площади
(
,
т.е. площадь арматуры в сечении элемента
должна быть не менее минимальной площади
(![]() ).
Для изгибаемых элементов минимальный
процент армирования сечения
).
Для изгибаемых элементов минимальный
процент армирования сечения![]() =
0,1%.
=
0,1%.
4. Типы задач по расчёту изгибаемых элементов
прямоугольного сечения
При расчёте прочности железобетонных конструкций выделяют два типа задач:
I тип – проверка прочности, заданного сечения элемента.
II тип – расчёт сечений:
а) подбор арматуры при известных размерах сечения элемента под заданный силовой фактор;
б) определение размеров поперечного сечения элемента и арматуры в нём под заданный силовой фактор.
ЛЕКЦИЯ 8
РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ТАВРОВОГО СЕЧЕНИЯ
С ОДИНОЧНОЙ АРМАТУРОЙ
Общие сведения
2. Расчёт изгибаемых элементов таврового сечения с полкой в растянутой зоне
3. Расчёт изгибаемых элементов таврового сечения с полкой в сжатой зоне
1. Общие сведения
Тавровые сечения встречаются в практике строительства в виде отдельных элементов - балок, а так же в составе конструкций - в монолитных ребристых и сборных панельных перекрытиях. Тавровое сечение состоит из полки – горизонтального и ребра – вертикального элементов. Полка может находиться в сжатой или растянутой зонах (рис. 8а, 8б).
Несущая способность железобетонного элемента не зависит от площади сечения бетона растянутой зоны. Поэтому в сравнении с прямоугольным сечением тавровое сечение значительно выгоднее, т.к. при одной и той же несущей способности бетона расходуется меньше вследствие сокращения размеров растянутой зоны. По той же причине тавровое сечение с полкой в сжатой зоне более целесообразно т.к. полка в растянутой зоне не повышает несущей способности элемента.
а) б)
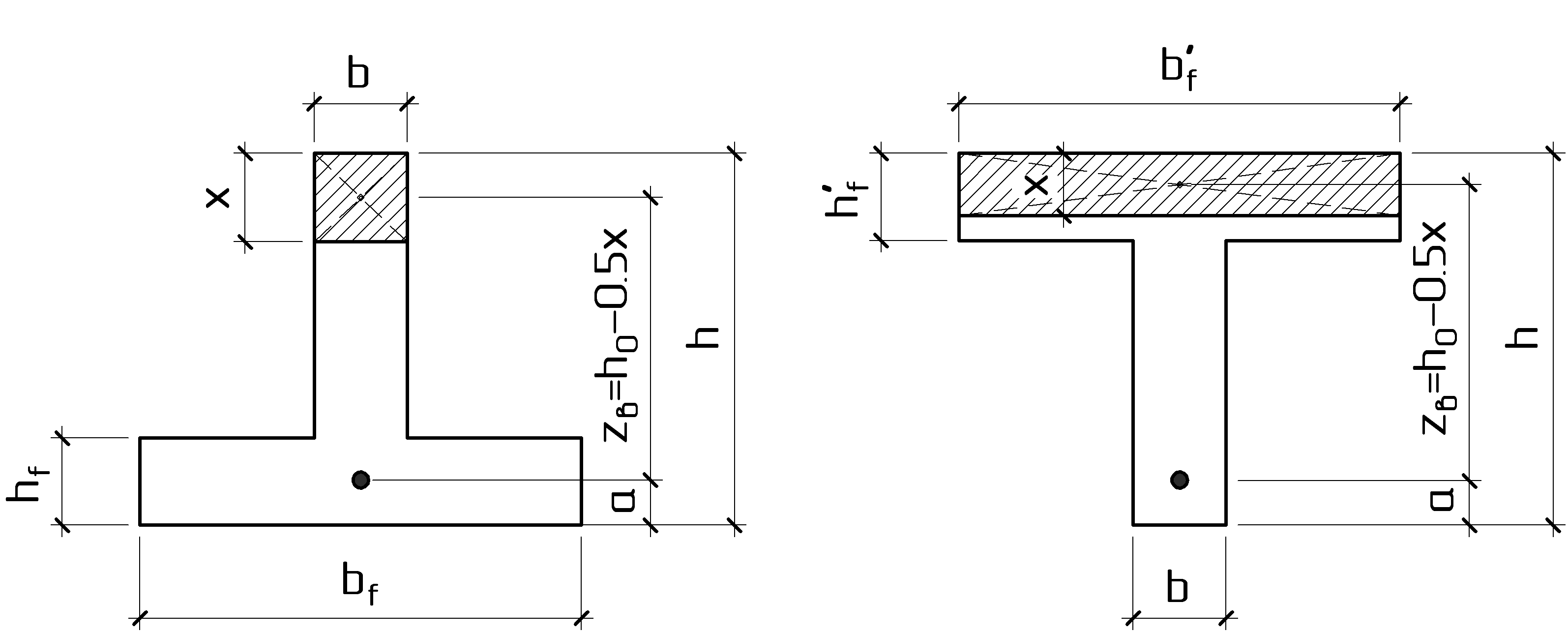
Рисунок 8.1 – Тавровые сечения в отдельных балках:
а – балка с полкой в растянутой зоне; б – балка с полкой в сжатой зоне
а)

б)
в)
Рисунок 8.2 – Тавровые сечения в составе перекрытий
а – тавровое сечение пустотной плиты;б – тавровое сечение в составе монолитного ребристого перекрытия; в – тавровое сечение в составе сборного перекрытия
2. Расчёт изгибаемых элементов таврового сечения
с полкой в растянутой зоне
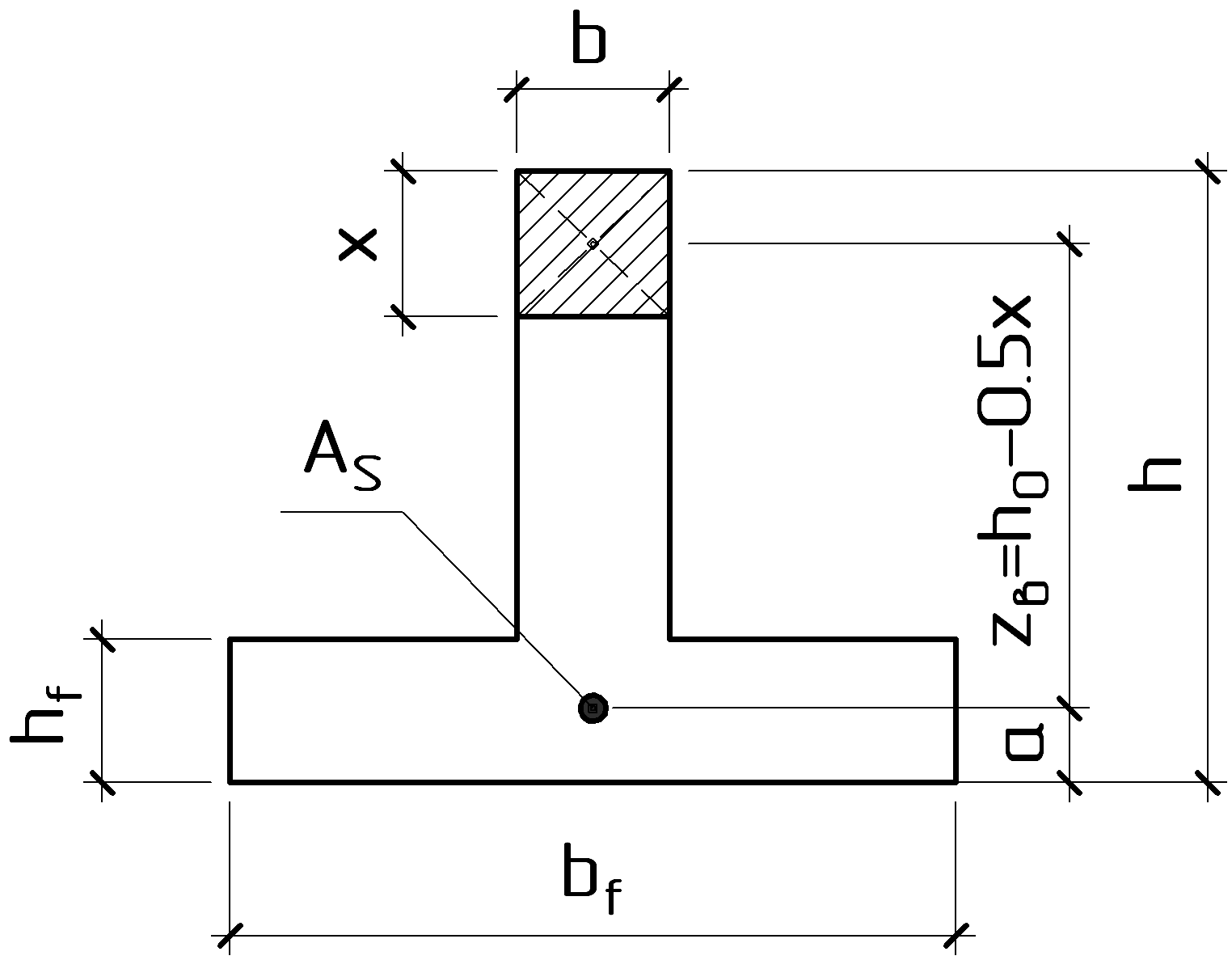
Рисунок 8.3 – К расчёту тавровых сечений с полкой в растянутой зоне
В
данном случае полка находится в растянутой
зоне. Растянутый бетон в расчёте не
учитывают, так как в нём имеются трещины.
Поэтому расчёт прочности таких элементов
выполняют как прямоугольных сечений с
размерами
![]() .
.
3. Расчёт изгибаемых элементов таврового сечения
с полкой в сжатой зоне
При расчёте изгибаемых элементов таврового сечения с полкой в сжатой зоне в зависимости от положения нейтральной оси возможны два случая расчёта:
-
нейтральная ось находится в
пределах полки
![]() (1 случай);
(1 случай);
-
нейтральная ось находится в
пределах ребра![]() >
>![]() (2 случай).
(2 случай).
1) Определение случая расчёта

Рисунок 8.4 – Схема усилий при определении случая расчёта
изгибаемых элементов таврового сечения
Предположим,
что нейтральная ось проходит по низу
полки, т.е. вся полка сжата и тогда
![]() .
.
Равнодействующие нормальных напряжений в сжатом бетоне и в растянутой арматуре равны:
![]() ,
,
![]() .
.
Плечо
внутренней пары сил
![]() .
.
Рассмотрим
равновесие элемента (рис. 15) под действием
изгибающего момента от нагрузки
![]() и внутренних усилий, возникающих в
сжатом бетоне
и внутренних усилий, возникающих в
сжатом бетоне![]() и растянутой арматуре
и растянутой арматуре![]() .
.
1.
![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Если
![]() ,
то
,
то![]() ,
т.е. нейтральная ось находится в пределах
полки и будем иметь 1 случай расчёта
тавровых сечений.
,
т.е. нейтральная ось находится в пределах
полки и будем иметь 1 случай расчёта
тавровых сечений.
Если
![]() >
>![]() ,
то
,
то![]() >
>![]() ,
т.е. нейтральная ось находится в пределах
ребра и будем иметь 2 случай расчёта
тавровых сечений.
,
т.е. нейтральная ось находится в пределах
ребра и будем иметь 2 случай расчёта
тавровых сечений.
Данные уравнения применяют для определения случай расчёта тавровых сечений при решении I типа задач – проверки прочности, заданного сечения элемента.
2.![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Выражение
![]() представляет собой изгибающий момент,
воспринимаемый сжатой полкой.
представляет собой изгибающий момент,
воспринимаемый сжатой полкой.
Если![]() ,
то
,
то![]() ,
т.е. нейтральная ось находится в пределах
полки и будем иметь 1 случай расчёта
тавровых сечений.
,
т.е. нейтральная ось находится в пределах
полки и будем иметь 1 случай расчёта
тавровых сечений.
Если
![]() >
>![]() ,
то
,
то![]() >
>![]() ,
т.е. нейтральная ось находится в пределах
ребра и будем иметь 2 случай расчёта
тавровых сечений.
,
т.е. нейтральная ось находится в пределах
ребра и будем иметь 2 случай расчёта
тавровых сечений.
Данные уравнения применяют для определения случай расчёта тавровых сечений при решении II типа задач – расчёта сечений элемента.
