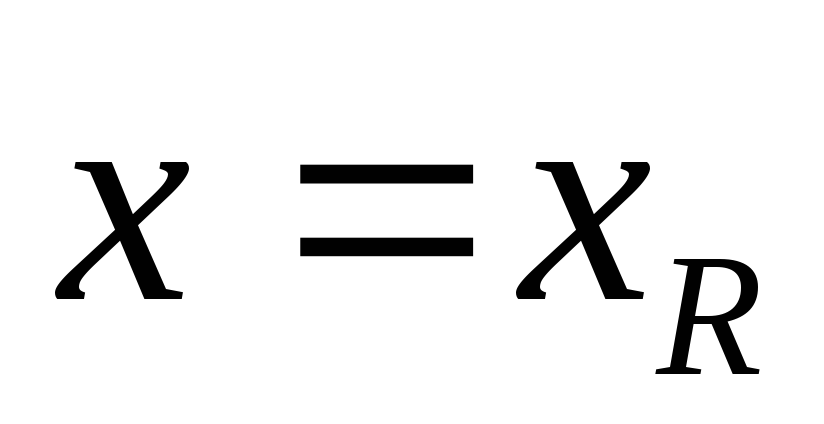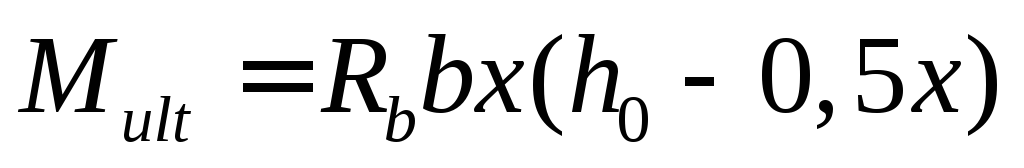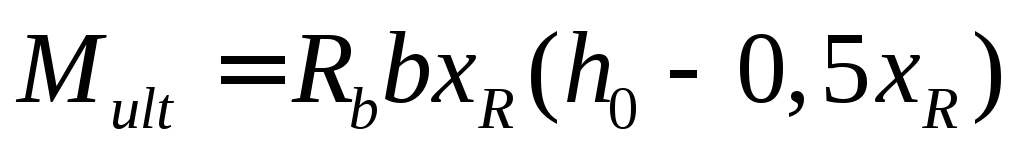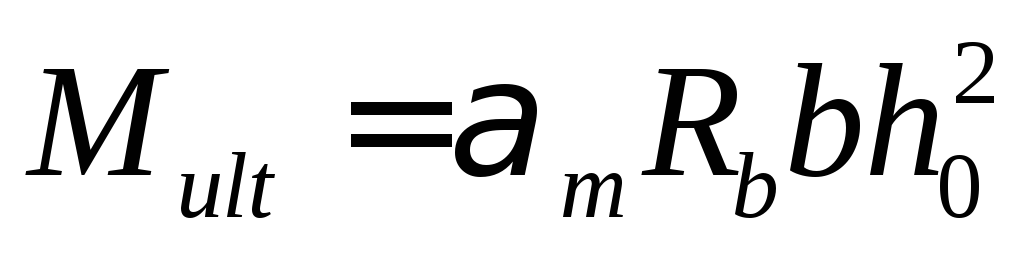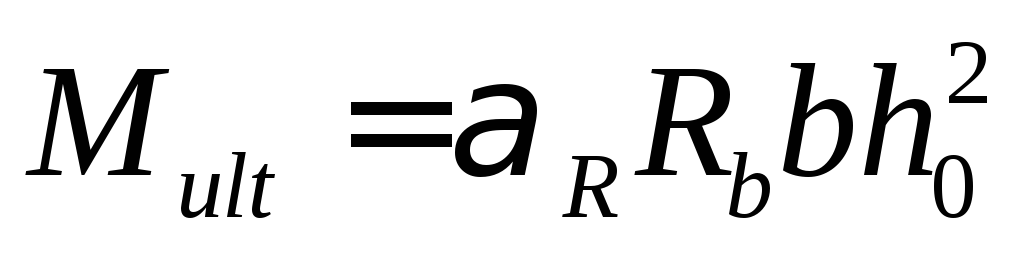- •И.В. Молев основы железобетонных конструкций
- •1.1. Определение и сущность железобетона
- •1.2. Достоинства и недостатки железобетона.
- •1.3. Виды железобетонных конструкций и область их применения железобетона.
- •1.4. Краткие исторические сведения о возникновении и развитии железобетона.
- •2. Структура (строение) бетона
- •3. Усадка бетона и начальные напряжения
- •4. Прочность бетона
- •1.5. Классы и марки бетона
- •6. Деформативность бетона
- •7. Модуль деформаций бетона
- •Арматура для железобетонных конструкций
- •1. Назначение арматуры и требования к ней
- •2. Виды арматуры
- •3. Физико-механические свойства арматурных сталей
- •4. Классификация арматуры по основным характеристикам. Сортамент арматуры
- •5. Сварные арматурные изделия
- •6. Соединения арматуры
- •Основные свойства железобетона
- •1. Общие сведения
- •2. Содержание арматуры
- •3. Значение трещиностойкости
- •4. Сцепление арматуры с бетоном
- •5. Анкеровка арматуры в бетоне
- •6. Усадка бетона при наличии арматуры
- •7. Ползучесть бетона при наличии арматуры
- •8. Коррозия железобетона и меры защиты от неё
- •9. Защитный слой бетона и минимальные расстояния между стержнями
- •1. Методы расчёта железобетонных конструкций
- •2. Сущность метода расчета конструкций по предельным состояниям
- •3. Две группы предельных состояний
- •4. Расчётные факторы
- •5. Классификация нагрузок. Нормативные и расчётные нагрузки
- •6. Степень ответственности зданий и сооружений
- •7. Нормативные и расчётные сопротивления бетона
- •8. Нормативные и расчётные сопротивления арматуры
- •9. Структура расчётных формул
- •1. Три стадии напряжённо-деформированного состояния железобетонных элементов
- •2. Классификация изгибаемых элементов
- •2.2. Плиты
- •Расчет изгибаемых элементов на почность по сечениям нормальным к продольной оси элемента
- •1. Предпосылки расчёта на прочность по нормальным сечениям
- •2. Расчёт изгибаемых элементов прямоугольного сечения с одиночной арматурой
- •3. Понятие о минимальном проценте армирования
- •2. Расчёт изгибаемых элементов таврового сечения
- •2) Расчёт прочности изгибаемых элементов таврового сечения по I случаю расчёта
- •3) Расчёт прочности изгибаемых элементов таврового сечения по II случаю расчёта
- •Расчет изгибаемых элементов на почность
- •2. Расчёт изгибаемых элементов по сжатой бетонной полосе между наклонными сечениями
- •3. Расчёт изгибаемых элементов по наклонным сечениям на действие поперечных сил (расчёт поперечной арматуры)
- •4. Расчёт изгибаемых элементов по наклонным
- •5. Конструктивные требования к постановке поперечной арматуры
- •1. Классификация сжатых элементов
- •2. Основы конструирования сжатых элементов
- •3. Расчёт элементов сжатых со случайным эксцентриситетом в форме центрального сжатия
- •Расчет внецентренно сжатых элементов
- •1. О характере работы и разрушения внецентренно сжатых элементов
- •Учёт влияния прогиба элемента
- •3. Расчёт сжатых элементов прямоугольного сечения в случае больших эксцентриситетов
- •4. Расчёт сжатых элементов прямоугольного сечения в случае малых эксцентриситетов
- •1. Общие сведения и конструктивные особенности
- •2. Расчёт прочности центрально растянутых элементов
- •3. Расчёт прочности элементов прямоугольного сечения, внецентренно растянутых в плоскости симметрии
2. Расчёт изгибаемых элементов прямоугольного сечения с одиночной арматурой
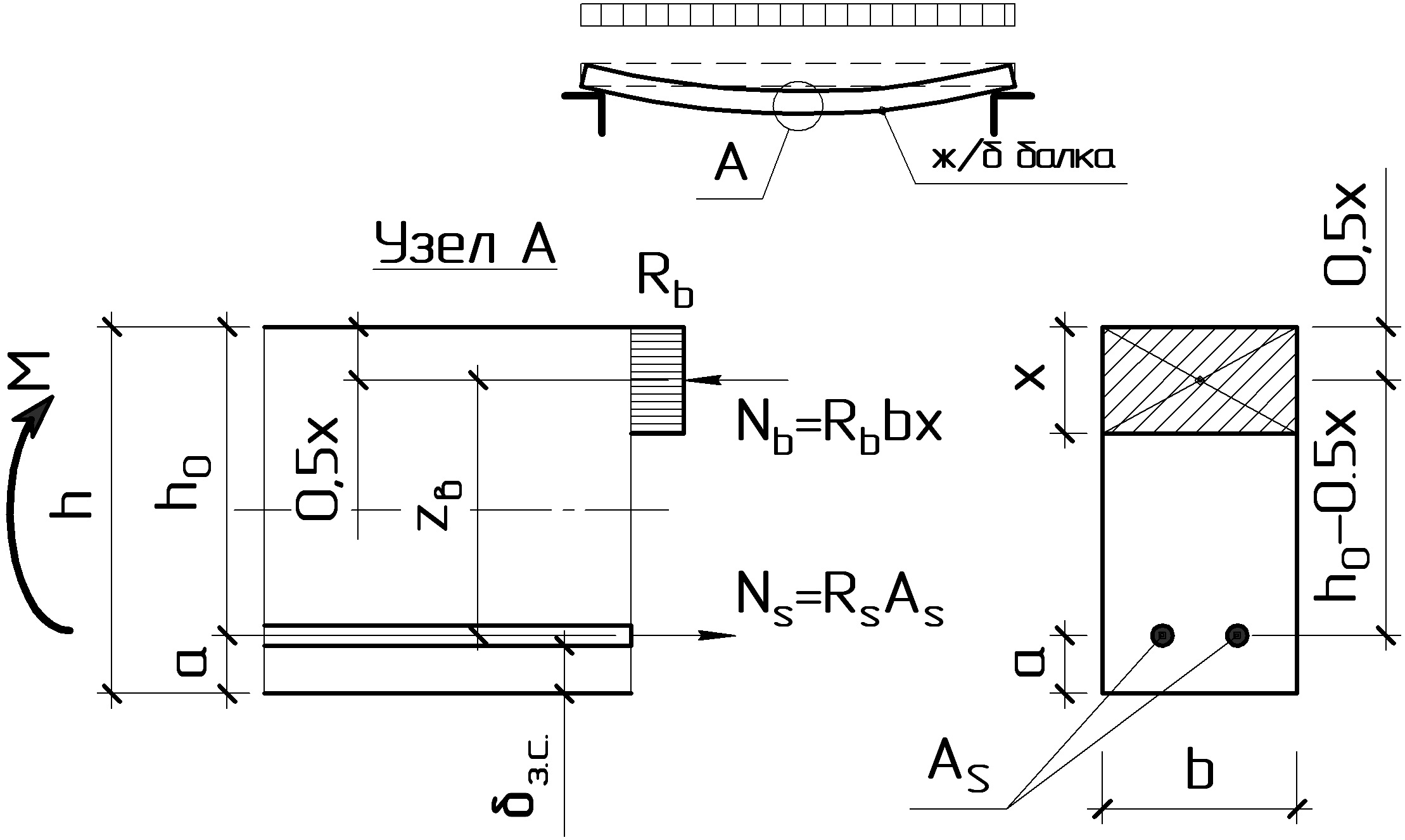
Рисунок 7.2 – Схема усилий при расчёте прочности изгибаемого элемента прямоугольного сечения с одиночной арматурой по нормальному сечению
Равнодействующие нормальных напряжений в сжатом бетоне и в растянутой арматуре определим по следующим формулам:
![]() ,
,
![]() .
.
В соответствие с рис. 11 плечо внутренней пары сил равно
![]() .
.
Рассмотрим равновесие элемента (рис. 11) под действием изгибающего момента от нагрузки М и внутренних усилий, возникающих в сжатом бетоне Nb и растянутой арматуре Ns.
1.
![]() - сумма проекций, действующих сил на ось
балки.
- сумма проекций, действующих сил на ось
балки.
![]() ;
;
![]() ;
;![]() .
.
Высота
сжатой зоны бетона равна
![]() .
.
Подставив
в эту формулу значение
![]() ,
получим
,
получим![]() и
и![]() выразим
отсюда площадь поперечного сечения
растянутой арматуры
выразим
отсюда площадь поперечного сечения
растянутой арматуры
![]() .
.
Из
выражения
![]() получим
получим![]() .
Обозначим отношение площади сечения
арматуры к площади сечения бетона
.
Обозначим отношение площади сечения
арматуры к площади сечения бетона![]() коэффициентом армирования сечения,
тогда
коэффициентом армирования сечения,
тогда![]() или
или![]() .
.
Процент
армирования сечения
![]() или
или![]() .
.
2.
![]() - сумма моментов, действующих сил
относительно центра тяжести растянутой
арматуры.
- сумма моментов, действующих сил
относительно центра тяжести растянутой
арматуры.
![]() ;
;
![]() ;
;![]() .
Выражение
.
Выражение![]() представляет собой выраженный через
параметры сжатого бетонапредельный
изгибающий момент,
воспринимаемый данным сечением, который
называют несущей
способность сечения.
представляет собой выраженный через
параметры сжатого бетонапредельный
изгибающий момент,
воспринимаемый данным сечением, который
называют несущей
способность сечения.
Тогда условие прочности изгибаемого элемента по нормальному сечению на действие изгибающего момента примет вид
![]() .
.
Таким образом, прочность элемента достаточна, если внешний расчётный изгибающий момент не превосходит расчётной несущей способности сечения, выраженной в виде обратно направленного момента внутренних сил.
Выполнив
подстановку
![]() ,
получим
,
получим
![]() .
.
Обозначив
![]() ,
получим условие прочности изгибаемого
элемента в другом виде
,
получим условие прочности изгибаемого
элемента в другом виде
![]() .
.
Приравняв
внешний и внутренний моменты
![]() ,
можно определить рабочую высоту сечения
элемента
,
можно определить рабочую высоту сечения
элемента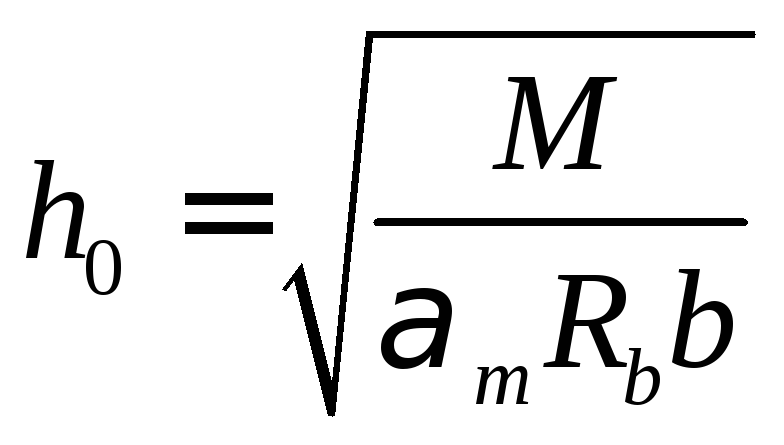 или
коэффициент
или
коэффициент![]() .
.
3.
![]() - сумма моментов относительно центра
тяжести сжатой зоны бетона.
- сумма моментов относительно центра
тяжести сжатой зоны бетона.
![]() ;
;
![]() ;
;![]() .
.
Выражение
![]() представляет собой выраженный через
параметры растянутой арматурыпредельный
изгибающий момент,
воспринимаемый данным сечением, который
тоже называют несущей
способность сечения.
представляет собой выраженный через
параметры растянутой арматурыпредельный
изгибающий момент,
воспринимаемый данным сечением, который
тоже называют несущей
способность сечения.
Тогда условие прочности изгибаемого элемента по нормальному сечению на действие изгибающего момента примет вид
![]() .
.
Выполнив
подстановку
![]() ,
получим условие прочности изгибаемого
элемента в другом виде
,
получим условие прочности изгибаемого
элемента в другом виде
![]() .
.
Коэффициент![]() определим
из выражения
определим
из выражения![]() ,
,
![]() .
.
Приравняв
внешний и внутренний моменты
![]() ,
можно определить площадь поперечного
сечения растянутой арматуры
,
можно определить площадь поперечного
сечения растянутой арматуры
![]() .
.
Приведённые
выше формулы справедливы при условии
![]() или
или![]() ,
т.е. когда разрушение элемента происходит
по растянутой зоне.
,
т.е. когда разрушение элемента происходит
по растянутой зоне.
Если
разрушение элемента происходит по
сжатой зоне, т.е.
![]() >
>![]() или
или![]() >
>![]() ,
томаксимальный
предельный изгибающий момент,
воспринимаемый прямоугольным сечением,
определяют
исходя из значения граничной высоты
сжатой зоны бетона
,
томаксимальный
предельный изгибающий момент,
воспринимаемый прямоугольным сечением,
определяют
исходя из значения граничной высоты
сжатой зоны бетона
![]() ,
которой соответствуют величины
,
которой соответствуют величины![]() ,
,![]() ,
,
![]() ,
тогда
,
тогда
![]() ,
,
![]() .
.
В
случае если
![]() определитьмаксимальный
предельный изгибающий момент через
характеристики арматуры по формулам
определитьмаксимальный
предельный изгибающий момент через
характеристики арматуры по формулам
![]() или
или![]() не
допустимо, так как растягивающие
напряжения в арматуре
не
допустимо, так как растягивающие
напряжения в арматуре![]() ,
что определяется совместностью
деформаций. Таким образом,в
случае
,
что определяется совместностью
деформаций. Таким образом,в
случае
![]() несущая способность арматуры на
растяжение используется не полностью.
Разрушение изгибаемого элемента в этом
случае носит мгновенный, хрупкий
характер, вследствие исчерпания несущей
способности бетона сжатой зоны, а
напряжения в арматуре при этом не
достигают предела текучести
несущая способность арматуры на
растяжение используется не полностью.
Разрушение изгибаемого элемента в этом
случае носит мгновенный, хрупкий
характер, вследствие исчерпания несущей
способности бетона сжатой зоны, а
напряжения в арматуре при этом не
достигают предела текучести
![]() .
.
Определение предельного изгибающего момента, воспринимаемого прямоугольным сечением, представим в таблице 1.
Таблица 1
-
1–й случай расчёта
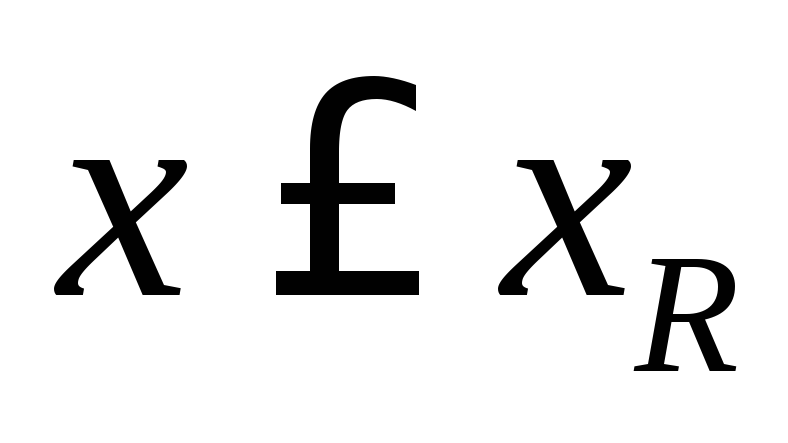
2–й случай расчёта
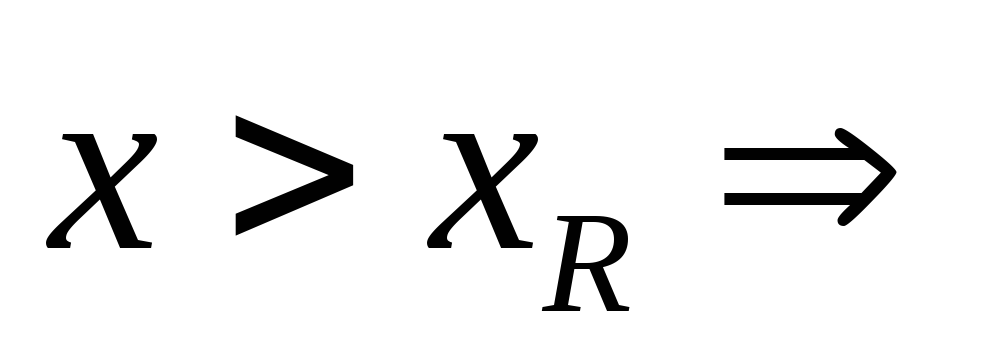 расчёт
выполняем при
расчёт
выполняем при