Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Нижегородский государственный архитектурно-строительный университет»

-------------------------------------------------------------------------------------------------

Институт экономики, управления и права

П.В. Столбов Математика

Часть III

Утверждено редакционно-издательским

советом университета в качестве

учебного пособия

Нижний Новгород

ННГАСУ

2013

ББК 22.1

С 81

Столбов П.В. Математика. Часть III [текст]: учебное пособие / П.В. Столбов; Нижегород. гос. архит.-строит. ун-т. – Н.Новгород: ННГАСУ, 2013. – 63 с.

ISBN 978-5-87941-880-0

Учебное пособие по математике предназначено для студентов всех специальностей и направлений.

ББК 22.1

ISBN 978-5-87941-880-0

© Столбов П.В., 2013

© ННГАСУ, 2013

§ 1. Дифференциальные уравнения первого порядка

В курсе математики средней школы изучались алгебраические уравнения, где неизвестными были числа. Сейчас мы переходим к рассмотрению так называемых дифференциальных уравнений, при решении которых находят неизвестные функции, удовлетворяющие заданным соотношениям, включающим операцию дифференцирования.

Рассмотрим для начала задачу о законе изменения скорости свободного падающего тела. Пусть тело массы падает с некоторой высоты. Учтем, что кроме силы тяжести, на него действует сила сопротивления воздуха. Запишем второй закон Ньютона

, (1.1)

предполагая, что сила сопротивления пропорциональна скорости в каждый момент временис коэффициентом пропорциональности. Уравнение (1.1), кроме неизвестной функции, содержит еще и ее производную. Это и есть дифференциальное уравнение.

Дадим общие определения. Дифференциальным уравнением первого порядка называется уравнение

, (1.2)

связывающее независимую переменную и искомую функциюс ее первой производной. Еслиможно явно выразить через оставшиеся переменные уравнения (1.2), то оно приобретает вид

. (1.3)

Решением дифференциального уравнения (1.2) называется всякая функция , которая при подстановке в уравнение (1.2) обращает его в тождество.

Можно убедиться, в частности, что функция

(1.4)

при любом значении постоянной удовлетворяет уравнению (1.1). Действительно, подставляя функцию (1.4) и ее производную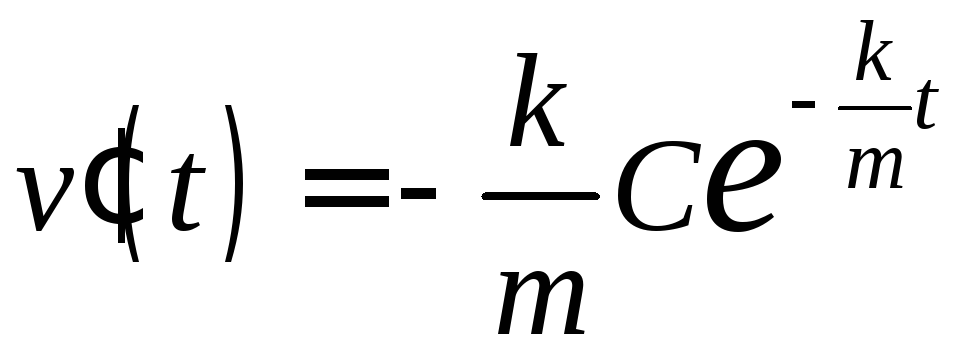в (1.1), получим тождество. Это означает, что функция вида (1.4) является решением уравнения (1.1).

Заметим, что мы нашли бесконечно много функций, удовлетворяющих дифференциальному уравнению (1.1) – каждому значению постоянной соответствует свое решение вида (1.4). Множество функций , обращающих уравнение (1.3) в тождество,называют общим решением дифференциального уравнения (1.3). Запись общего решения содержит произвольную постоянную . Заметим, что решение дифференциального уравнения может быть записано и в неявном виде.

Допустим, что в рассматриваемой задаче известна скорость тела в начальный момент времени . Обозначим её. Чтобы определить, как будет изменяться скорость тела в дальнейшем, выделим из найденного множества решений (1.4) только одно - то, которое соответствует начальному условию. Приииз множества решений (1.4) получим, откуда. Подставляя найденное значение постоянной в (1.4), получим закон изменения скоростипадающего тела при заданном начальном условии:

. (1.5)

Согласно последнему равенству, скорость падающего тела прибудет стремиться к величине. Отсюда, в частности, можно найти нужный коэффициент сопротивления(парашют), чтобы обеспечить приземление с допустимой скоростью. Функция (1.5) представляет собой так называемое частное решение уравнения (1.1), соответствующее начальному условию.

Частным решением уравнения (1.3) называется одна функция, удовлетворяющая самому уравнению и начальному условию. Задачу нахождения частного решения дифференциального уравнения (1.3), удовлетворяющего данному начальному условию , называютзадачей Коши. Если правая часть уравнения (1.3) непрерывна в некоторой области, содержащей начальную точку, и имеет непрерывную в этой области частную производную,то задача Коши имеет единственное решение. При этих условиях частное решение получается из общего решения при конкретном значении произвольной постоянной .

Процесс отыскания решения дифференциального уравнения называется его интегрированием, а график решения – интегральной кривой. Рассмотрим геометрическую интерпретацию решений уравнения (1.3) на конкретном примере. Пусть требуется найти частное решение дифференциального уравнения

, (1.6)

удовлетворяющего начальному условию

. (1.7)

Непосредственной подстановкой убеждаемся, что функция вида

(1.8)

обращает уравнение (1.6) в тождество. Она содержит произвольную постоянную и является общим решением уравнения (1.6). Построив в плоскостиграфики этих функций при различных значениях. мы получим семейство парабол (См. рис.1).

Чтобы выделить из этого семейства интегральных кривых конкретную параболу, соответствующую условию (1.7), рассмотрим точку с координатами . Через нее проходит парабола семейства (1.8), для которой. Соответствующее решениеявляется искомым частным решением.

Переходим к рассмотрению конкретных видов дифференциальных уравнений первого порядка и методов их решения.

Если правая часть дифференциального уравнения (1.3) может быть записана в виде произведения функций двух функцийи, зависящих от переменныхисоответственно, то есть, то уравнение называют дифференциальным уравнением с разделяющимися переменными.

Учитывая, что , перепишем последнее уравнение в виде

или .

Умножая обе части последнего уравнения на , получим вид уравнения, (1.9)

в котором каждая из переменных инаходится в той части уравнения, где ее дифференциал. Считаяизвестной функцией от, равенство (1.9) можно рассматривать как равенство двух дифференциалов и интегрировать обе части уравнения (1.9). Полученные при этом функциии будут отличаться постоянным слагаемым:. Мы записали соотношение, связывающее решение , независимую переменнуюи произвольную постоянную, это соотношение и представляет собой общее решение дифференциального уравнения (1.3).

Уравнение с разделяющимися переменными, записанное исходно в дифференциальной форме

,

решается аналогично.

Решим для примера дифференциальное уравнение

. (1.10)

Функцию в правой части уравнения можно представить в виде произведенияи переписать уравнение (1.10):

или .

Умножая обе части последнего уравнения на функцию , получим. Интегрируя, находим, или, откуда– общее решение уравнения (1.10), где– произвольная постоянная.

Решим далее задачу Коши: найдем решение уравнения

, (1.11)

при условии, что

. (1.12)

Дифференциальное уравнение (1.11) с разделяющимися переменными запишем в виде

.

Умножая обе части последнего уравнения на , разделим переменные:.

Интегрируя , находим, или, где– произвольная постоянная.

Итак, общее решение уравнения (1.11) имеет вид

.

Учет начального условия (1.12) дает , откуда. Следовательно, решение задачи Коши записывается в виде

или .

Рассмотрим далее линейные дифференциальные уравнения первого порядка, которые, по определению, имеют вид

. (1.13)

Решение уравнения (1.13) будем искать в виде произведения

(1.14)

двух неизвестных функций и, тогда

. (1.15)

Подставив в уравнение (1.13) вместо иравенства (1.14) и (1.15) соответственно, получим

,

или . (1.16)

Рассмотрение вместо одной неизвестной функции двух функцийидает возможность ввести для одной из них, в частности, дополнительное условие, которое упростит уравнение. Оно состоит в требовании обращения выраженияв нуль, то есть

. (1.17)

Уравнение (1.17) является дифференциальным уравнением с разделяющимися переменными и. Его запишем в видеили. Умножая обе части последнего уравнения на, разделяем переменные:. Интегрируем

и находим одно из решений уравнения (1.17), например, при постоянной . Это решение обозначим. Для второй неизвестной функциииз (1.16) получим уравнение.Снова разделяем переменные и, интегрируя, находим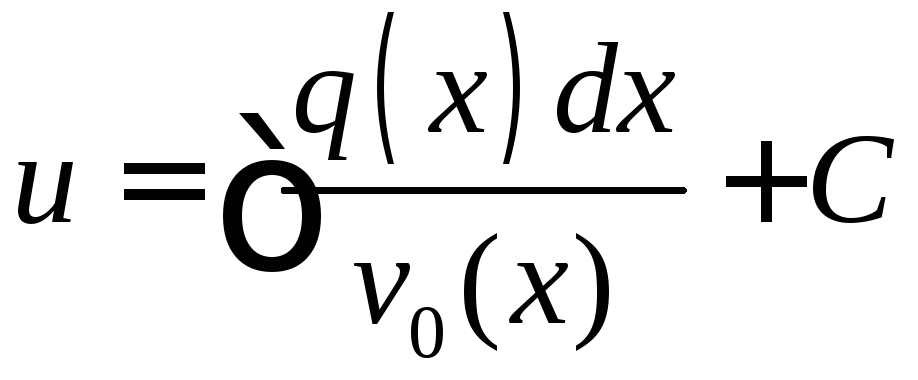, где– произвольная постоянная.

Подставляя найденные ив функцию (1.14), получаем решение уравнения (1.13) в виде.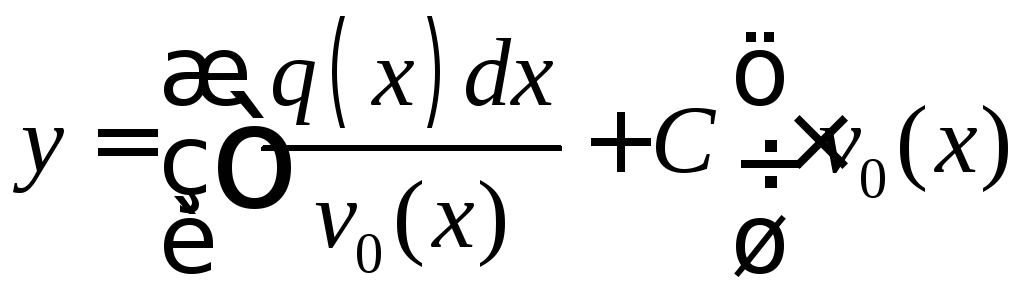

Найдем для примера общее решение уравнения

(1.18)

В нем по условию ,. Подставив в уравнениеи, получим,

или . (1.19)

В качестве функции возьмем одно решениеуравнения при значении. Перепишем его в виде, разделим переменныеи, интегрируя, находим. Приполучим. (1.20)

Подставим функцию (1.20) в (1.19), получим или.

Снова разделяя переменные и интегрируя,

находим , (1.21)

где – произвольная постоянная.

Подставляя найденные функции (1.20) и (1.21) в равенство , получим общее решение данного уравнения (1.18)

.