40

§ 7. Параметрическое задание кривых на плоскости.

Пусть заданы две функции одного аргумента

(17)

где (в частности допускается ). При каждом значении числа и будем понимать как координаты некоторой точки на плоскости, причем эта точка, вообще говоря, меняется вместе с изменением , описывая некоторую кривую . В этом случае систему уравнений (17) называют параметрическими уравнениями линии , а аргумент называют параметром.

Переход от параметрических уравнений к уравнению осуществляется исключением параметра из системы уравнений (17).

Рассмотрим несколько примеров.

1. – известные параметрические уравнения прямой, проходящей через точку с направляющим вектором , .

2. . Исключая параметр , получаем , то есть уравнение параболы, .

3. Уравнения – уравнения окружности радиуса , т.к. , .

4. Уравнения , – являются параметрическими уравнениями эллипса.

5. Циклоида.

Пусть по прямой без скольжения катится круг радиуса . Кривая, описываемая фиксированной точкой круга, называется циклоидой. Уравнения циклоиды .

t

Рис. 19.

6. Астроида.

Пусть по окружности радиуса внутри нее катится без скольжения круг радиуса . Траектория, которую описывает фиксированная точка, лежащая на границе подвижного круга, называется астроидой.

x

-а

a

O

Рис. 20.

Уравнения астроиды , .

7. Кардиоида.

Пусть по окружности радиуса вне ее катится без скольжения круг того же радиуса . Кривая, которую описывает фиксированная точка подвижного круга, называется кардиоидой.

a

O

Рис. 21.

Уравнения кардиоиды , .

§ 8. Кривые в полярной системе координат.

Рассмотрим полярную систему координат на плоскости. Пусть нам задан полюс и полярная ось. Для произвольной точки на плоскости обозначим через расстояние от точки до точки , а через – угол, на который нужно повернуть полярную ось до совмещения с лучом.

М

О

Р

Рис. 22.

Числа , называются полярными координатами точки . Число называют полярным радиусом (всегда ), а число называют полярным углом точки . Полярный радиус для любой точки определяется однозначно, а полярный угол – с точностью до , где – целое число.

Пусть на плоскости задана полярная и правая декартова прямоугольная система координат.

0

Рис. 23.

Пусть – произвольная точка плоскости, имеющая декартовы координаты и полярные координаты . Рассмотрим радиус вектор точки . Сравнивая координаты, получим формулы перехода от декартовых координат к полярным:

, .

Формулы перехода от полярных координат к декартовым можно записать в виде:

, .

При можно вычислить .

Кривую в полярных координатах задают в виде уравнения или явного уравнения в виде .

Рассмотрим несколько примеров кривых, заданных в полярных координатах.

1. Уравнение , где – постоянное число, задает окружность радиуса , центр которой совпадает с полюсом .

2. Уравнение определяет луч, исходящий из полюса и составляющий угол с полярной осью. – произвольное число.

3. Выведем полярное уравнение окружности радиуса в случае, когда полюс лежит на ней, а полярная ось проходит через центр окружности.

Рис. 24.

Возьмем произвольную точку на окружности. Треугольник прямоугольный. Получаем уравнение окружности в виде .

4. Покажем, что уравнение и полярных координатах определяет окружность радиуса . Подставим выражения для и через и в уравнение: . Умножая обе части уравнения на 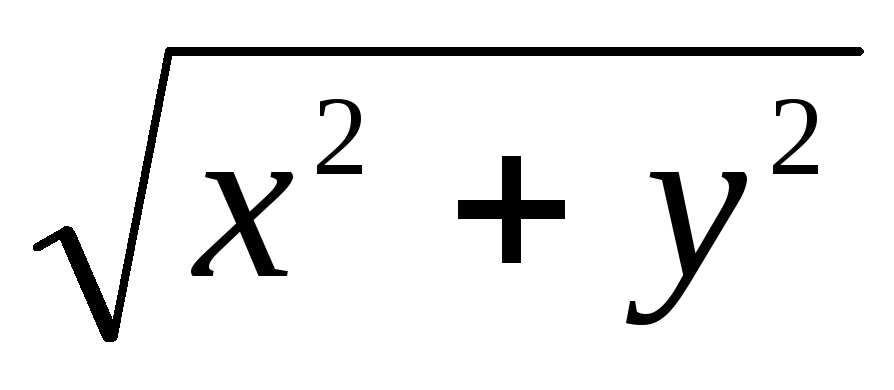, получим или . Это уравнение окружности радиуса 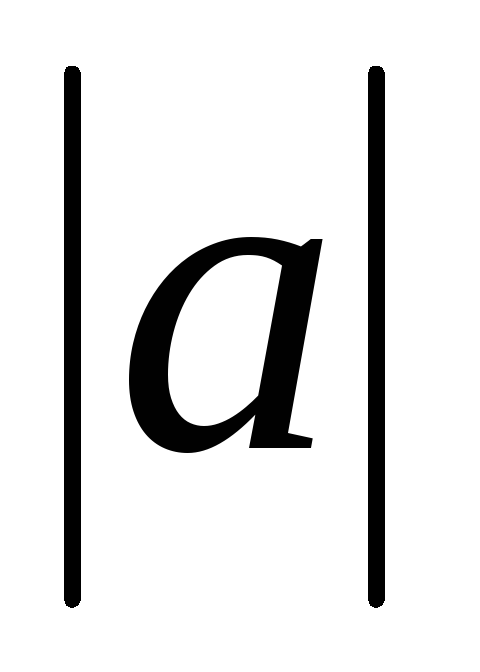с центром в точке .

5. Пусть в декартовой системе координат заданы прямые , . Уравнения этих прямых в полярной системе координат , .

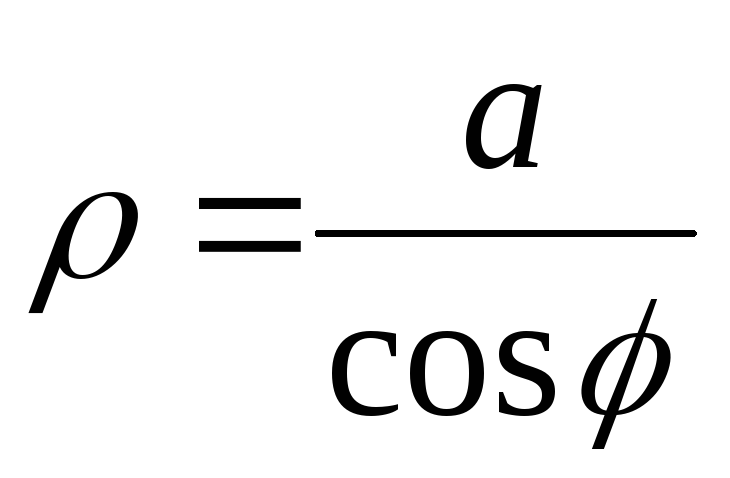6. Рассмотрим уравнение , . Переход к декартовым координатам здесь довольно громоздкий и приводит к алгебраическому уравнению высокой степени. Поэтому посмотрим эту кривую, исходя из качественных соображений.

Период правой части уравнения равен , поэтому достаточно построить кривую для значений полярного угла из интервала . По свойствам функции , см. рис. 22, видно, что полярный радиус монотонно возрастает при и при монотонно убывает. При правая часть уравнения отрицательна, для этих значений точек кривой нет. Для остальных значений кривая получается при повороте на угол части кривой, расположенной между лучами и , рис. 24.

Рис. 25.