
- •Г.М. Грушевский, о.О. Иваев, с.К. Романов, в.В. Ходыкин Железобетонные конструкции
- •Введение
- •1. Основные физико-механические свойства бетона, стальной арматуры и железобетона
- •1.1. Бетон
- •1.1.1. Общие сведения
- •1.1.2. Структура (строение) бетона
- •1.1.3. Усадка бетона и начальные напряжения
- •1.1.4. Прочность бетона
- •1.1.5. Классы и марки бетона
- •1.1.6. Деформативность бетона
- •1.1.7. Модуль деформаций бетона
- •1.2. Арматура для железобетонных конструкций
- •1.2.1. Назначение арматуры и требования к ней
- •1.2.2. Виды арматуры
- •1.2.3. Физико-механические свойства арматурных сталей
- •1.2.4. Классификация арматуры по основным характеристикам. Сортамент арматуры
- •1.2.5. Сварные арматурные изделия
- •1.2.6. Соединения арматуры
- •1.3. Железобетон
- •1.3.1. Общие сведения
- •1.3.2. Содержание арматуры
- •1.3.3. Значение трещиностойкости
- •1.3.4. Сцепление арматуры с бетоном
- •1.3.5. Анкеровка арматуры в бетоне
- •1.3.6. Усадка бетона при наличии арматуры
- •1.3.7. Ползучесть бетона при наличии арматуры
- •1.3.8. Коррозия железобетона и меры защиты от неё
- •1.3.9. Защитный слой бетона и минимальные расстояния между стержнями
- •2. Экспериментальные основы теории сопротивления железобетона и методы расчета железобетонных конструкций
- •2.1. Общие сведения
- •2.2. Три стадии напряжённо-деформированного состояния железобетонных элементов
- •2.3. Методы расчёта железобетонных конструкций
- •2.4. Метод расчёта железобетонных конструкций по предельным состояниям
- •2.4.1. Сущность метода
- •2.4.2. Две группы предельных состояний
- •2.4.3. Расчётные факторы
- •2.4.4. Классификация нагрузок. Нормативные и расчётные нагрузки
- •2.4.5. Степень ответственности зданий и сооружений
- •2.4.6. Нормативные и расчётные сопротивления бетона
- •2.4.7. Нормативные и расчётные сопротивления арматуры
- •2.4.8. Структура расчётных формул
- •2.4.9. Общий способ расчёта прочности железобетонных элементов
- •Литература
- •Содержание
1.3.7. Ползучесть бетона при наличии арматуры
В результате стеснённого деформирования бетона ползучесть железо-бетонных элементов при обычных процентах армирования примерно в 1,5...2 раза меньше, чем неармированных.
Вследствие ползучести бетона напряжённое состояние железобетонного элемента, находящегося под постоянной нагрузкой, изменяется в течение времени за счёт перераспределения усилий между бетоном и арматурой. Процесс перераспределения усилий особенно интенсивно протекает в течение первых 3...4 месяцев после нагружения, а затем в течение длительного времени (более года) затухает.
Количественный анализ перераспределения напряжений (усилий) вследствие ползучести бетона можно провести, рассмотрев работу железобетонной призмы (короткой, в которой не ощущается сильно влияние продольного изгиба) с симметрично расположенной арматурой на осевое сжатие при действии постоянной длительной нагрузки (рис. 30, а). Для любого момента работы железобетонной призмы справедливо следующее уравнение равновесия внешних и внутренних сил:
![]() (1.33)
(1.33)
Условие совместности деформаций арматуры и бетона при этом будет выглядеть так:
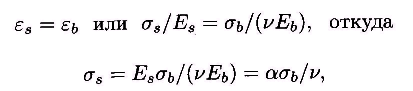 (1.34)
(1.34)
где v – коэффициент упругопластических деформаций бетона при сжатии.
Подставив
в (1.33) значение
![]() из
(1.34), получим:
из
(1.34), получим:
![]() (1.35)
(1.35)
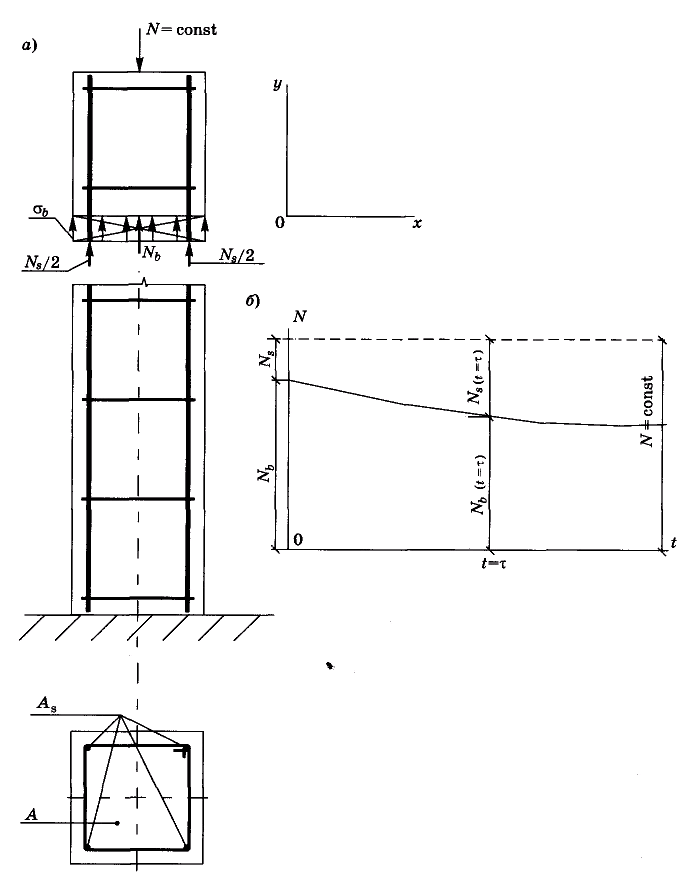
Рис. 30. Перераспределение усилий между арматурой и бетоном в сжатой железобетонной призме вследствие ползучести бетона:
а – схема работы железобетонной призмы под нагрузкой; б – характер изменения усилий в бетоне и арматуре при постоянной нагрузке в течение длительного времени
Из (1.35):
![]() (1.36)
(1.36)
Значение коэффициента v может изменяться от 1 (при мгновенном загружении элемента) до 0,15 (при очень длительном загружении и нагрузке, близкой к разрушающей).
Известно,
что
![]() здесь
здесь
![]() .
Таким
образом,
.
Таким
образом,
![]() с
течением
времени растет, a
v
уменьшается.
Следовательно, как видно из (1.36), при
уменьшении v
с течением
времени
с
течением
времени растет, a
v
уменьшается.
Следовательно, как видно из (1.36), при
уменьшении v
с течением
времени
![]() уменьшается.
При N
= const
это означает, что бетон в железобетонном
элементе с увеличением времени нагружения
разгружается, а продольная арматура
догружается. Графически это перераспределение
представлено на рис. 30, б.
уменьшается.
При N
= const
это означает, что бетон в железобетонном
элементе с увеличением времени нагружения
разгружается, а продольная арматура
догружается. Графически это перераспределение
представлено на рис. 30, б.
Расчёты и опыты показывают, что при действии на конструкцию эксплуатационных нагрузок напряжения в продольной арматуре сжатых железобетонных элементов возрастают в 2...3 раза вследствие ползучести бетона.
В коротких центрально сжатых железобетонных элементах ползучесть оказывает положительное влияние на их работу, обеспечивая более полное использование прочностных свойств бетона и арматуры. В гибких сжатых элементах, наоборот, ползучесть бетона вызывает увеличение начальных эксцентриситетов продольной силы, что может снизить их несущую способность.
В статически неопределимых конструкциях вследствие ползучести бетона может происходить выгодное перераспределение усилий (главным образом изгибающих моментов) между отдельными поперечными сечениями.
В некоторых других случаях ползучесть бетона может приводить к ухудшению работы железобетонной конструкции. Например, в изгибаемых элементах (балки, плиты) со временем значительно увеличиваются прогибы (примерно в 2...3 раза по сравнению с первоначальным), особенно при загружении бетона в раннем возрасте.
