Метод Крамера

Пусть дана система трех линейных уравнений:

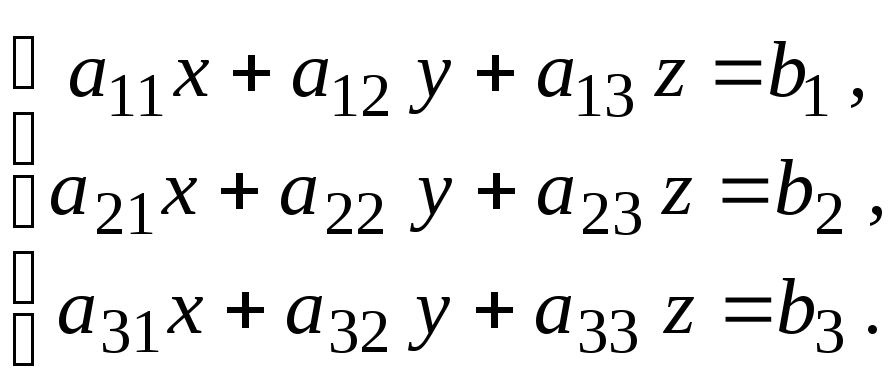(1)

Для решения системы линейных уравнений методом Крамера из коэффициентов при неизвестных составляется главный определитель системы . Для системы (1) главный определитель имеет вид .

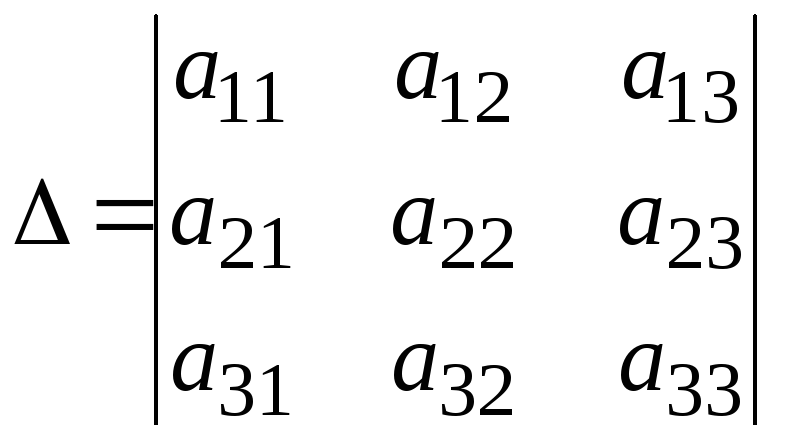Далее составляются определители по переменным ,,. Для этого в главном определителе вместо столбца коэффициентов при соответствующей переменной записывается столбец свободных членов, то есть

, ,.

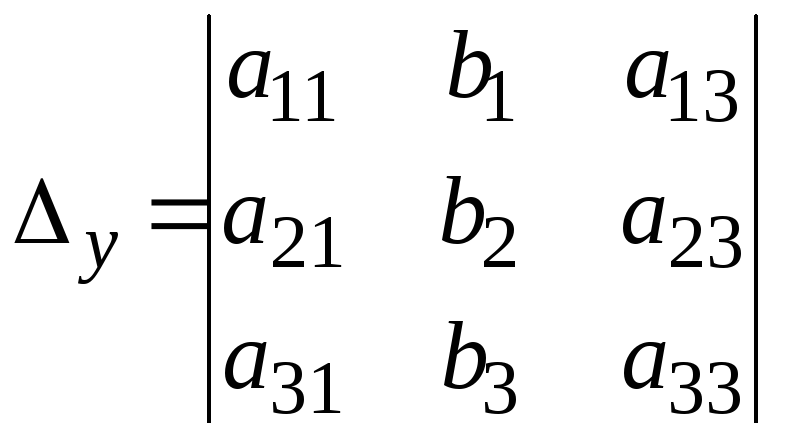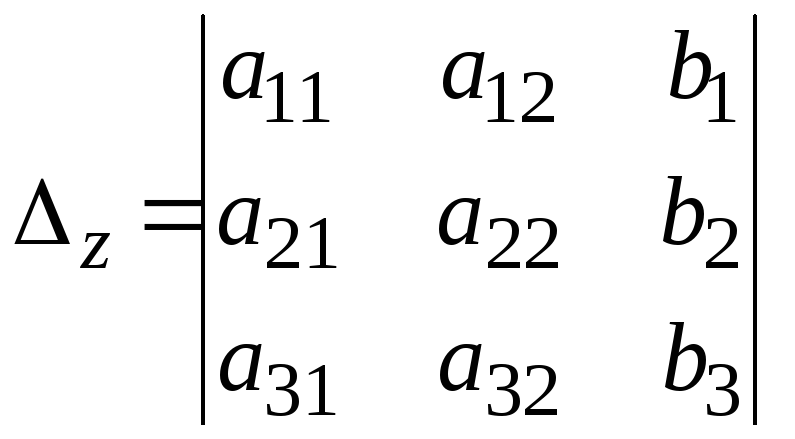Тогда решение системы находится по формулам Крамера

, ,

Следует отметить, что система имеет единственное решение , если главный определитель.Если же и = 0,= 0,= 0, то система имеет бесчисленное множество решений, найти которые по формулам Крамера нельзя. Если же и 0, или0,или0, то система уравнений несовместна, то есть решений не имеет.

Пример

Решить систему уравнений методом Крамера:

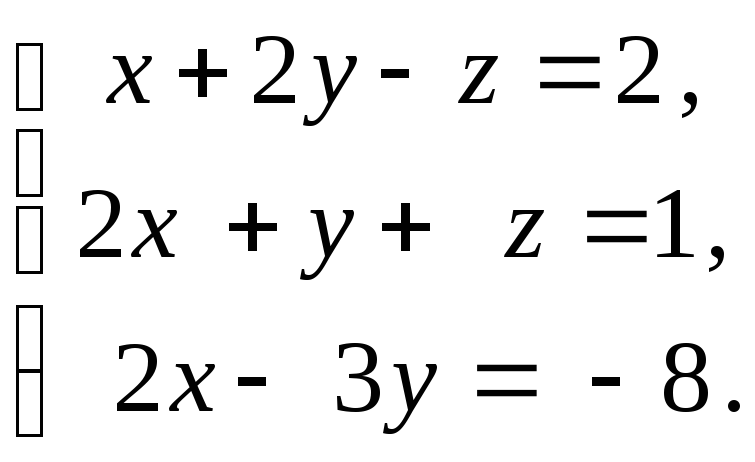
Решение:

1) Составим и вычислим главный определитель системы, состоящий из коэффициентов при неизвестных.

.

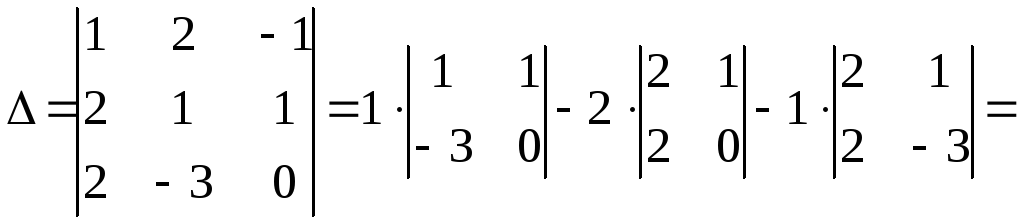
Следовательно, система имеет единственное решение.

2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в  столбцом из свободных членов.

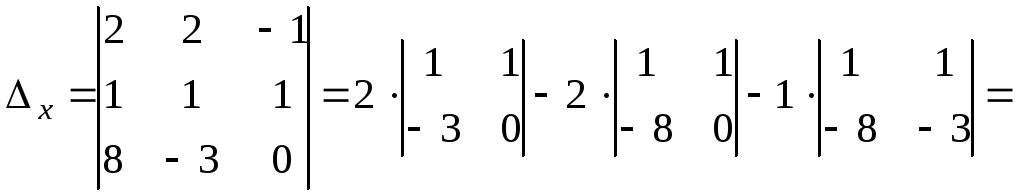
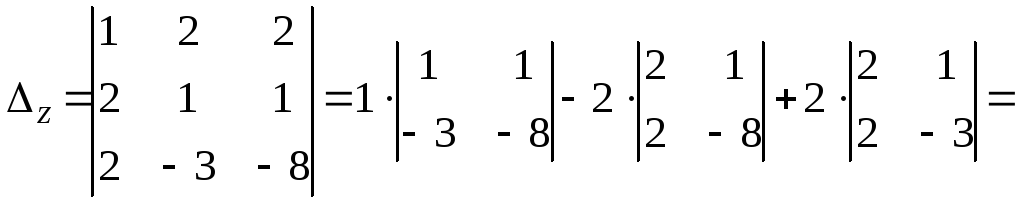
По формулам Крамера находим неизвестные:

, ,.

Сделаем проверку, чтобы убедиться в правильности решения

, т.е. .

, т.е.

, т.е.

Ответ: .

Пример

Решить систему уравнений методом Крамера:

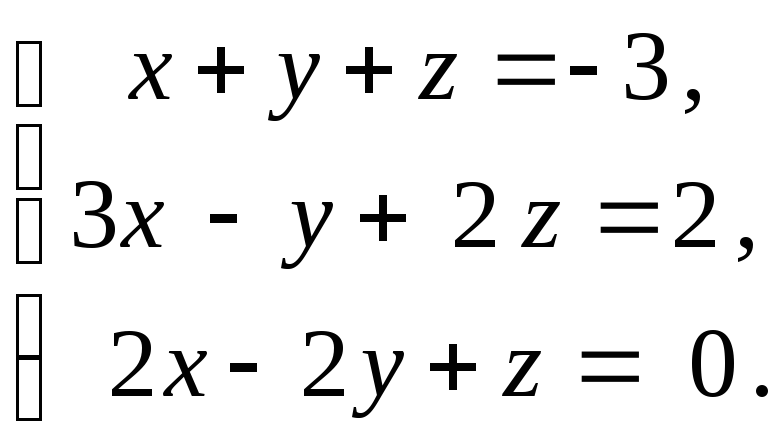
Решение:

1) Составим и вычислим главный определитель системы из коэффициентов при неизвестных:

.

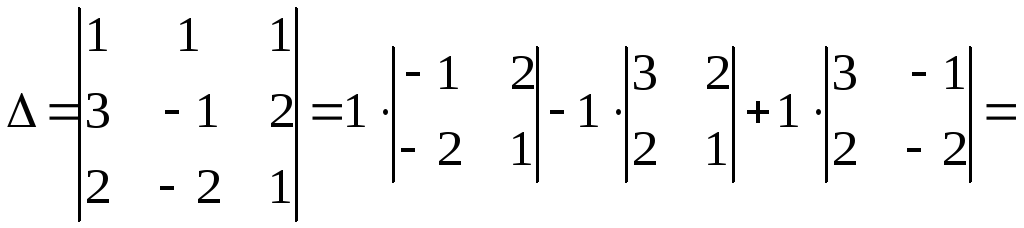
Следовательно, система не имеет единственного решения.

2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в  столбцом из свободных членов:

.

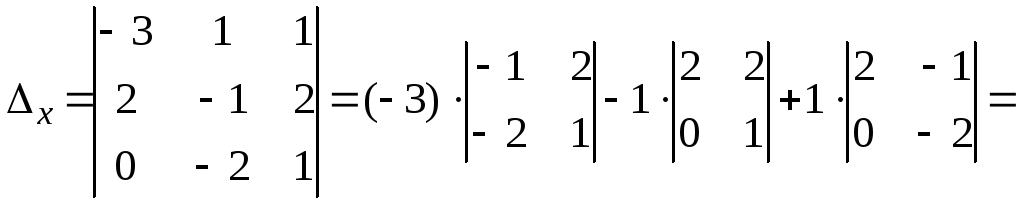
, , следовательно, система несовместна.

Ответ: система несовместна.

Метод Гаусса

Метод Гаусса состоит из двух этапов. Первый этап заключается в последовательном исключении переменных из уравнений системы при помощи действий, не нарушающих равносильности системы. Например, рассмотрим два первых уравнения системы 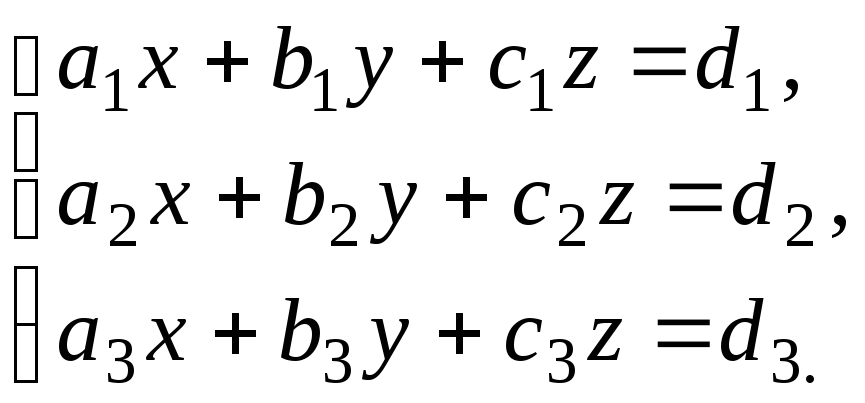(1).

(1)

Необходимо путем сложения этих двух уравнений получить уравнение, в котором отсутствует переменная . Умножим первое уравнение на, а второе на () и сложим полученные уравнения

+

Заменим коэффициент перед y, z и свободный член на ,исоответственно, получим новую пару уравнений

Заметим, что во втором уравнении отсутствует переменная x.

Проведя аналогичные действия над первым и третьим уравнениями системы (1), а затем над полученными в результате сложения вторым и третьим уравнениями, преобразуем систему (1) к виду

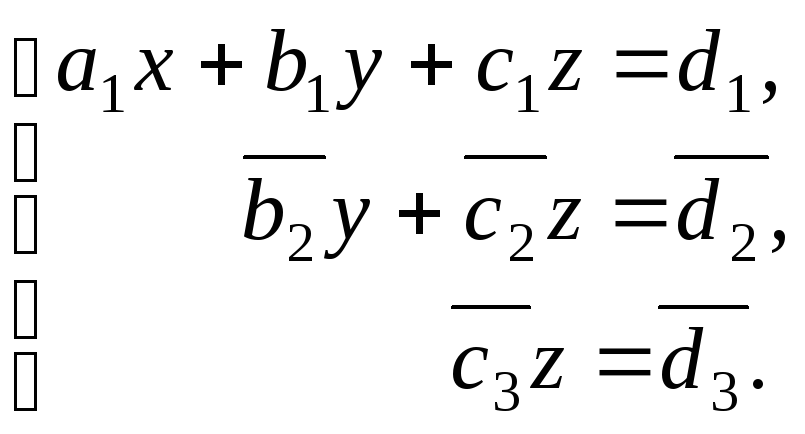(2)

Такой результат возможен, если система имеет единственное решение. В этом случае решение находится при помощи обратного хода метода Гаусса (второй этап). Из последнего уравнения системы (2) находим неизвестную переменную z, затем из второго уравнения находим y, а x соответственно из первого, подставляя в них уже найденные неизвестные.

Иногда в результате сложения двух уравнений суммарное уравнение может принять один из видов:

А) , где. Это означает, что решаемая система несовместна.

Б) , то есть. Такое уравнение исключается из системы, в результате число уравнений в системе становится меньше, чем число переменных, и система имеет бесчисленное множество решений, нахождение которых будет показано на примере.

Пример

Решить систему методом Гаусса:

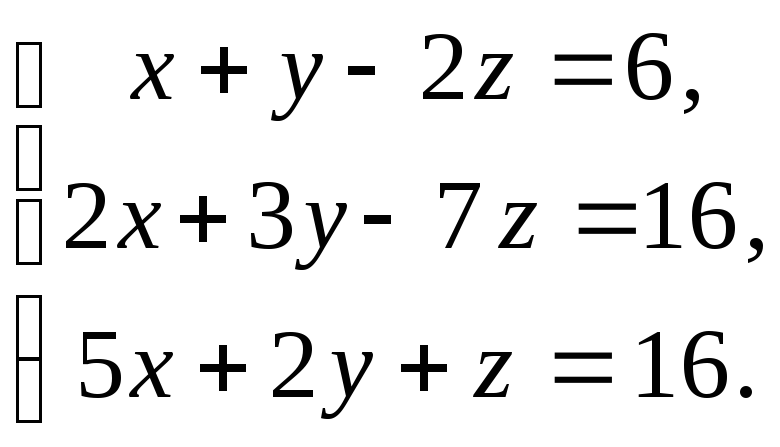
Решение:

Рассмотрим следующий способ осуществления первого этапа решения методом Гаусса. Запишем три строки коэффициентов при неизвестных и свободных членов, соответствующих трем уравнениям системы. Свободные члены отделим от коэффициентов вертикальной линией, а под третьей строкой проведем горизонтальную прямую.

Первую строку, которая соответствует первому уравнению системы, обведем – коэффициенты в этом уравнении останутся неизменными. Вместо второй строки (уравнения) надо получить строку (уравнение), где коэффициент при равен нулю. Для этого все числа первой строки умножим на (–2) и сложим с соответствующими числами второй строки. Полученные суммы запишем под горизонтальной чертой (четвертая строка). Для того чтобы вместо третьей строки (уравнения) также получить строку (уравнение), в которой коэффициент приравен нулю, умножим все числа первой строки на (–5) и сложим с соответствующими числами третьей строки. Полученные суммы запишем пятой строкой и проведем под ней новую горизонтальную черту. Четвертую строку (или пятую – по выбору) обведем. Выбирается строка с меньшими коэффициентами. В этой строке коэффициенты останутся неизменными. Вместо пятой строки надо получить строку, где уже два коэффициента равны нулю. Умножим четвертую строку на 3 и сложим с пятой. Сумму запишем под горизонтальной чертой (шестая строка) и обведем ее.

Все описанные действия изображены в таблице 1 при помощи арифметических знаков и стрелок. Обведенные в таблице строки запишем снова в виде уравнений (3) и, применив обратный ход метода Гаусса, найдем значения переменных x, y и z.

Таблица 1

1	1	-2	6	*(-2)	*(-5)
2	3	-7	16
5	2	1	16
0	1	-3	4	*( 3)
0	-3	11	-14
0	0	2	-2

Восстанавливаем систему уравнений, полученную в результате наших преобразований:

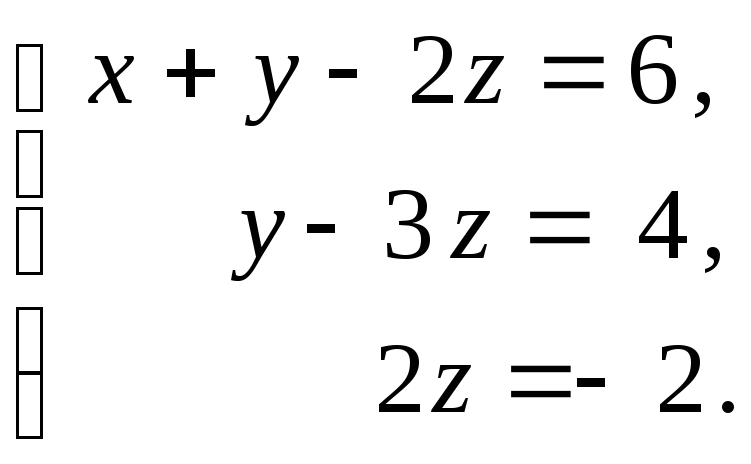(3)

Обратный ход метода Гаусса

Из третьего уравнения находим.

Во второе уравнение системы подставим найденное значение, получимили.

Из первого уравнения , подставляя уже найденные значения переменных, получаем, то есть.

Чтобы убедиться в правильности решения, проверку необходимо сделать во всех трех уравнениях системы.

Проверка:

, получим

, получим

, получим

значит, система решена верно.

Ответ: ,,.

Пример

Решить систему методом Гаусса:

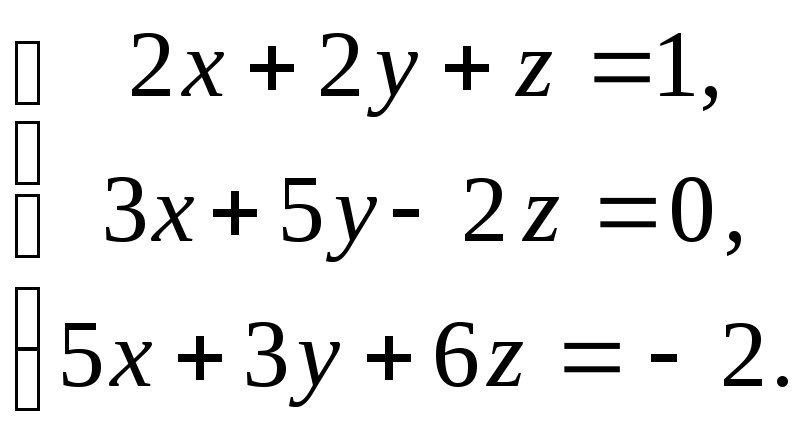
Решение:

Порядок действий в этом примере аналогичен порядку в предыдущем примере, а конкретные действия указаны в таблице 2.

Таблица2

2	2	1	1	*(-3)	*(-5)
3	5	-2	0	*2
5	3	6	-2	*2
0	4	-7	-3
0	-4	7	-9
0	0	0	-12

В результате преобразований получим уравнение вида , следовательно, заданная система несовместна.

Ответ: система несовместна.

Пример

Решить систему методом Гаусса:

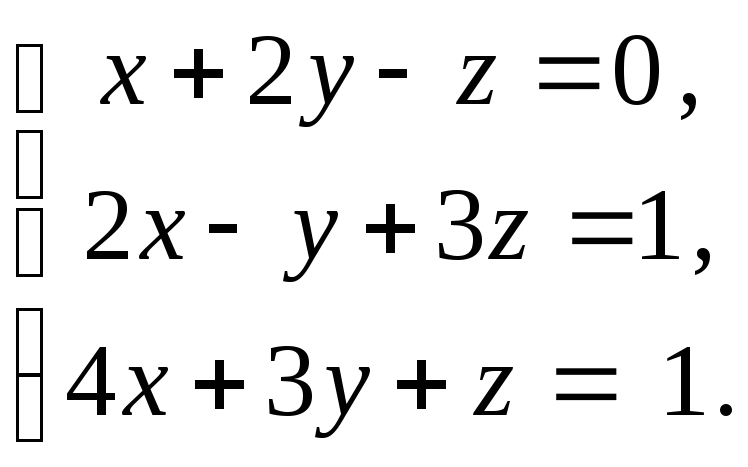
Решение:

Таблица 3

1	2	-1	0	*(-2)	*(-4)
2	-1	3	1
4	3	1	1
0	-5	5	1	*(-1)
0	-5	5	1
0	0	0	0

В результате преобразований получим уравнение вида , которое исключается из рассмотрения. Таким образом, имеем систему уравнений, в которой число неизвестных 3, а число уравнений 2.

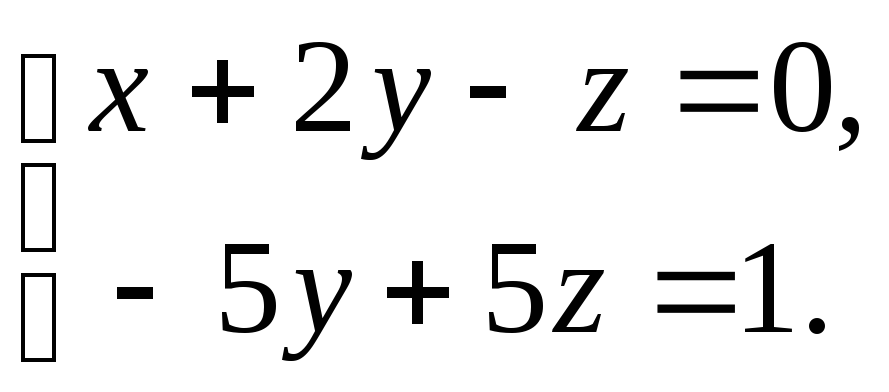
Система имеет бесчисленное множество решений. Чтобы отыскать эти решения, введем одну свободную переменную. (Число свободных переменных всегда равно разности между числом неизвестных и числом уравнений, оставшихся после преобразования системы. В нашем случае 3 – 2 = 1).

Пусть – свободная переменная.

Тогда из второго уравнения найдем , откуда, а затем найдемx из первого уравнения или.

Таким образом, ;;.

Сделаем проверку в уравнениях, которые не участвовали в нахождении и, то есть во втором и в третьем уравнениях первоначальной системы.

Проверка:

или , получаем.

или , получаем.

Система решена верно. Давая произвольной постоянной различные значения, будем получать различные значенияx, y и z.

Ответ: ;;.

21