
Глава 1. Элементы линейной алгебры
§ 1. Матрицы и определители
Для решения многих сельскохозяйственных задач используются элементы алгебры матриц и векторной алгебры, особенно при разработке и использовании баз данных: при работе с ними почти вся информация хранится и обрабатывается в матричной форме.
Пример
Дана таблица распределения ресурсов по отдельным отраслям экономики
|
Ресурсы |
Отрасли экономики | |
|
промышленность |
сельское хозяйство | |
|
Электроэнергия |
5,3 |
4,1 |
|
Трудовые ресурсы |
2,8 |
2,1 |
|
Водные ресурсы |
4,8 |
5,1 |
Эта
таблица может быть записана в компактной
форме в виде матрицы распределения
ресурсов по отраслям: А
В
этой записи, например, матричный элемент
![]() показывает, сколько электроэнергии
потребляет промышленность, а элемент
показывает, сколько электроэнергии
потребляет промышленность, а элемент![]() – сколько трудовых ресурсов потребляет
сельское хозяйство.
– сколько трудовых ресурсов потребляет
сельское хозяйство.
Определение
1. Матрицей
размера (типа) mn
называется
таблица чисел
 строки
строки![]()
…
столбцы
Величины
![]() ,
стоящие в строках и столбцах матрицы,
называются элементами матрицы; это
могут быть числа, переменные, функции
и пр.В
обозначении элемента
,
стоящие в строках и столбцах матрицы,
называются элементами матрицы; это
могут быть числа, переменные, функции
и пр.В
обозначении элемента
![]() первый индексi
указывает номер строки, а второй индекс
j
указывает
номер столбца,
на пересечении которых стоит данный
элемент.
первый индексi
указывает номер строки, а второй индекс
j
указывает
номер столбца,
на пересечении которых стоит данный
элемент.
Определение 2. Квадратной матрицей n-ого порядка называется матрица размера n n:

Например,
квадратная матрица второго порядка
имеет следующий вид:
 ,
,
а
квадратная матрица третьего порядка –
 .
.
Виды матриц
Матрица,
состоящая из одной строки, называется
матрицей
(вектором)–строкой
А![]() ,
а из одного столбца –матрицей
(вектором)–столбцом А
,
а из одного столбца –матрицей
(вектором)–столбцом А .
.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Например,
А – диагональная матрица третьего порядка.
– диагональная матрица третьего порядка.
Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка, она обозначается буквой Е.
Например,
Е – единичная матрица третьего порядка.
– единичная матрица третьего порядка.
Линейные операции над матрицами
1.
Сумма
матриц.
Суммой матриц А
и В
одинакового размера называется матрица
С = А + В
того же размера, каждый элемент которой
равен сумме соответствующих элементов
матриц А
и В,
т.е.
![]() ,
где
,
где![]() ;
;![]() .
.
Например,
А![]() ,В
,В![]() ,
тогда
,
тогда
С
= А + В
![]()
![]() .
.
2.
Умножение матрицы на действительное
число.
Произведением матрицы на действительное
число
![]() называется матрица
называется матрица![]() ,
каждый элемент которой получен умножением
соответствующего элемента матрицыА
на число
,
каждый элемент которой получен умножением
соответствующего элемента матрицыА
на число
![]() ,
т.е.
,
т.е.![]() для
для![]() ;
;![]() .
.
Например,
А![]() ,
,![]() ,
тогда
,
тогда
![]() =
=![]()
![]() .
.
3.
Умножение матриц.
Умножение матрицы А
на матрицу В
определено, когда число столбцов первой
матрицы равно числу строк второй матрицы.
В данном случае, матрица А
называется согласованной с матрицей
В.
Тогда произведением матриц
![]() называется такая матрица
называется такая матрица![]() ,
каждый элемент которой равен сумме
произведений элементовi-ой
строки матрицы А
на соответствующие элементы j-го
столбца матрицы В,
т.е.
,
каждый элемент которой равен сумме
произведений элементовi-ой
строки матрицы А
на соответствующие элементы j-го
столбца матрицы В,
т.е.
![]() ,
,
![]() ;
;
![]() .
.
Например, вычислим произведение матриц
А=![]() ,В=
,В= .
.
Найдем
размер матрицы–произведения:
![]() .
.
Вычислим
элементы матрицы
![]() ,
умножая элементы каждой строки матрицы
на соответствующие элементы столбцов
матрицыВ
следующим образом:
,
умножая элементы каждой строки матрицы
на соответствующие элементы столбцов
матрицыВ
следующим образом:
![]() ==
==
![]() .
.
Произведение
матриц
![]() на
на![]() не существует, так как количество
столбцов первой матрицы
не существует, так как количество
столбцов первой матрицы![]() равное 3 не совпадает с количеством
строк второй матрицы
равное 3 не совпадает с количеством
строк второй матрицы![]() равным 2, то есть матрицы не являются
согласованными.
равным 2, то есть матрицы не являются
согласованными.
Произведение матриц некоммутативно АВ ≠ ВА.
Матрицы, для которых выполняется переместительный закон АВ = ВА, называются коммутативными.
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
А + В = В + А 2) (А + В) + С = А + (В + С)
(А + В)= А+ В 4) А(В + С) = АВ + АС
(А+В)С = АС + ВС 6) (АВ) = (А)В = А(В)
А(ВС) = (АВ)С.
Матричное произведение вектор-строки на вектор-столбец называется скалярным произведением.
Пример
Предприятие выпускает ежесуточно четыре вида колбасных изделий, основные производственно-экономические показатели, которых приведены в таблице
|
Вид изделия |
Количество изделий |
Расход сырья, кг/изд. |
Норма времени изготовления, ч/изд. |
Цена изделия, ден. ед./изд. |
|
1 |
20 |
5 |
10 |
30 |
|
2 |
50 |
2 |
5 |
15 |
|
3 |
30 |
7 |
15 |
45 |
|
4 |
40 |
4 |
8 |
20 |
Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.
Решение: По данным таблицы составим четыре вектора, характеризующие весь производственный цикл:
 , s
=
, s
=![]() ,t
,t
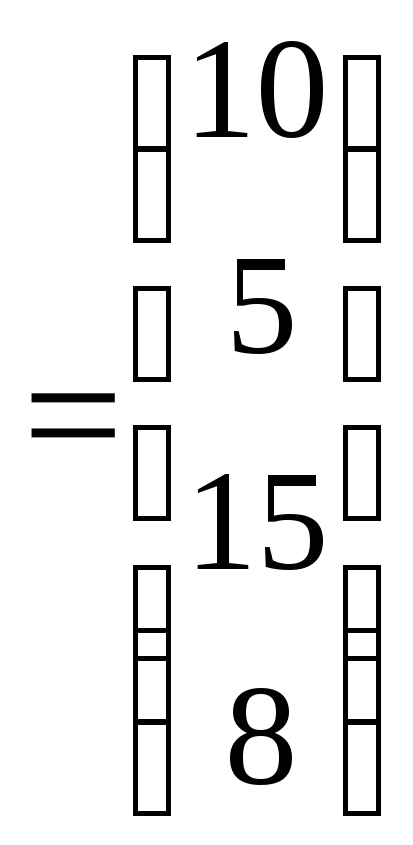 ,p
,p
 ,
,
где q – вектор ассортимента; s – вектор расхода сырья; t – вектор затрат рабочего времени; p – ценовой вектор.
Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента q на три других вектора:
расход
сырья S
= q![]() s
s![]() кг,
кг,
затраты
рабочего времени T
= q![]() t
t![]() ч,
ч,
стоимость выпускаемой продукции предприятия
P
= q![]() p
p
![]() ден. ед.
ден. ед.
Пример
Предприятие выпускает четыре вида изделий молочной продукции с использованием четырех видов сырья. Нормы расхода сырья даны как элементы матрицы А:
Вид сырья
 1
2 3 4
1
2 3 4
А

Требуется найти затраты сырья каждого вида при заданном плане выпуска каждого вида изделия: соответственно 60, 50, 35 и 40 ед.
Решение:
Составим вектор-план выпуска продукции
q
=![]() .
.
Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду; этот вектор затрат вычисляется как произведение матрицы А на вектор q:
Аq
=
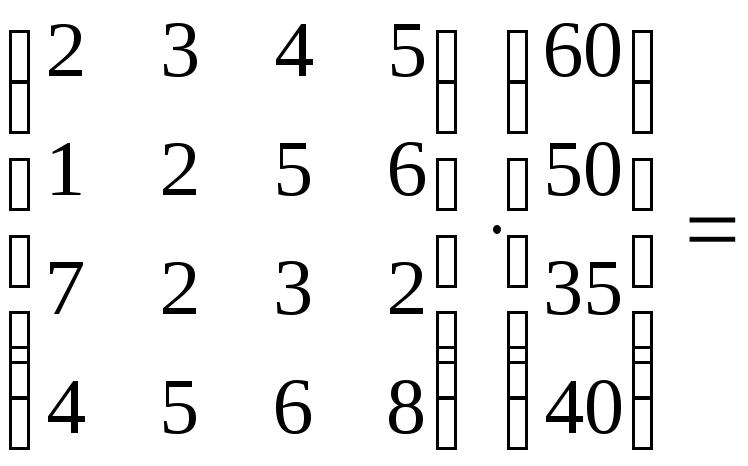
![]() .
.
Определение
3. Число
![]() называетсяопределителем
второго порядка,
соответствующим матрице
называетсяопределителем
второго порядка,
соответствующим матрице
 .
.
Пример
Найти
определитель матрицы
![]() .
.
Решение:
![]() .
.
Определение 4.
Число

называется
определителем
третьего порядка,
соответствующим матрице
 .
.
Пример
Найти
определитель матрицы
 .
.
Решение:

