
- •Глава 1. Двойные интегралы
- •§1. Определение двойного интеграла и критерий интегрируемости
- •§2. Свойства двойных интегралов
- •3. Вычисление двойного интеграла сведением к повторному интегралу
- •§4. Замена переменных в двойном интеграле
- •§5. Переход к полярным координатам. Вычисление
- •Глава 2. Тройные интегралы
- •1.Гамма-функция
- •2. Бета-функция
- •3. Формула Стирлинга
2. Бета-функция
Эйлером предложен также несобственный интеграл
 (3)
(3)
как
функция параметров
 ,
которую называютбета-функцией.
Представим интеграл (3) в виде суммы двух
слагаемых
,
которую называютбета-функцией.
Представим интеграл (3) в виде суммы двух
слагаемых
 ,
,
где
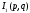 имеет особенность только в точке
имеет особенность только в точке ,
а
,
а - только в точке
- только в точке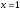 .
.
Поскольку
для любого
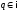 функция
функция положительна, непрерывна и ограничена
на отрезке
положительна, непрерывна и ограничена
на отрезке ,
то существуют постоянные
,
то существуют постоянные ,
что
,
что для всех
для всех и всех
и всех .
Поэтому, как и в предыдущем пункте,
убеждаемся, что интеграл
.
Поэтому, как и в предыдущем пункте,
убеждаемся, что интеграл сходится для всех
сходится для всех только при
только при .
.
Аналогично,
функция
 положительна, непрерывна и ограничена
на отрезке
положительна, непрерывна и ограничена
на отрезке для любого
для любого ,
и, следовательно, существуют
,
и, следовательно, существуют ,
что
,
что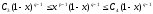 для всех
для всех и всех
и всех .
.
Поэтому
несобственный интеграл
 сходится для каждого
сходится для каждого только при
только при .
.
Окончательно,
бета-функция
 определена только для
определена только для и
и .
.
Совершая
в интеграле (3) замену переменной
интегрирования
 ,
получим
,
получим
 . (4)
. (4)
Формула (4) указывает на свойство симметричности бета-функции Эйлера.
Интегрируя
в (3) по частям и используя разложение
 ,
получим
,
получим

откуда
 (5)
(5)
В
силу симметричности функции
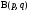 имеем также
имеем также
 (5’)
(5’)
Формулы (5) и (5’) называют функциональными уравнениями для бета-функции.
Если
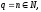 то согласно (5)
то согласно (5)

Но

Так что
 (6)
(6)
Если
 то (6) принимает вид
то (6) принимает вид

Так
как
 то мы доказали частный случай
то мы доказали частный случай
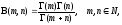
замечательной формулы Эйлера

Гамма-функция и бета-функция, как и экспоненциальная функция, играют фундаментальную роль в математике и её приложениях.
Сформулируем без доказательств несколько важных свойств этих функций.
Для
любого ,
, выполняется равенство
выполняется равенство ,
называемое формулой
дополнения. Из
этого, в частности, следует, что
,
называемое формулой
дополнения. Из
этого, в частности, следует, что
 и,
следовательно,
и,
следовательно, .
.
Бета-функция допускает ещё представление в виде интеграла

Часто используется интеграл (Вы встретите его при вычислении двойных, тройных интегралов при переходе к полярным, сферическим или цилиндрическим координатам)

Сведём его к значениям эйлеровых интегралов:

3. Формула Стирлинга
К настоящему моменту времени свойства гамма-функции изучены достаточно глубоко. В частности, для неё доказано следующее асимпототическое представление
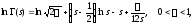 (7)
(7)
называемое
формулой
Стирлинга.
Для натуральных
 ,
когда
,
когда ,
формула (7) после несложных преобразований
принимает вид
,
формула (7) после несложных преобразований
принимает вид
 где
где

