Глава 2. Тройные интегралы

Рассмотрим кубируемое множество . Считаем, что оно ограничено конечным числом кусочно-гладких поверхностей . Разбиениена частитакже осуществляется кусочно- гладкими поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции, разбиениямножествана частии для выбранных точекинтегральную сумму

,

где обозначает объем части.

Определение. Пусть такое число, что .

Тогда мы говорим, что функция интегрируема на множестве , числоестьинтеграл функции по множествуи обозначаем это так:.

Как и в случае двойного интеграла, выполняются свойства 1-6. Полезное упражнение - переформулировать их для тройного интеграла .

Теорема 2.1. Ограниченная на кубируемом множестве функция интегрируема тогда и только тогда, когда

(На экзамене ограничиваемся формулировкой).

Из этого критерия следует теорема.

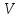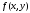Теорема 2.2. Если функция непрерывна на кубируемом множестве , то интегрируема на этом множестве.

(На экзамене достаточно формулировки).

Точно также можно убедиться в том, что если точки разрыва лежат на конечном числе кусочно-гладких поверхностей, лежащих наи разбивающихна кубируемые области, тоинтегрируема на.

Вычисление тройного интеграла производится по следующему правилу.

Теорема 2.3. Пусть задана следующими неравенствами:

,

где — квадрируемая область на плоскости,непрерывные функции. Тогда

.

Замечание. Если область задана неравенствами, где— непрерывные функции, то

Сформулируем общую теорему о замене переменных.

Теорема 2.4. Пусть отображение устанавливает взаимно однозначное соответствие между областямии, причем функции— непрерывно дифференцируемые и ни в одной точке.Пусть всюду в области

Пусть — непрерывная функция. Тогда

.

Как и для двойного интеграла, теорема остается верной в случае нарушения ее условий на множестве нулевого объема.

Пример 1. Переход к цилиндрическим координатам. Он осуществляется с помощью функций: .

При этом якобиан равен

.

Пример 2. Переход к сферическим координатам осуществляется функциями .

Якобиан преобразования равен

(разложение определителя по 3-й строке)

(выделение общих множителей у столбцов)

.

Часто используется интеграл (вы встретите его при вычислении двойных, тройных интегралов при переходе к сферическим или цилиндрическим координатам)

Сведем его к значениям эйлеровых интегралов см. приложение 3:

|=

Приложение 2. Эйлеровы интегралы

1.Гамма-функция

Рассмотрим несобственный интеграл

(1)

как функцию от s и выясним область ее определения. Для этого представим интеграл (1) в виде суммы несобственных интегралов

.

Поскольку для всехи всех, а эталонный интегралсходится при; т.е. при, и расходится при, то, по признакам сравнения несобственных интегралов, интегралсходится при всехи расходится при.

Поскольку для любогоисходится, то по аналогичному признаку сравнения заключаем, что несобственный интегралсходится при всех.

Окончательно, несобственный интеграл (1) сходится только при ; т.е.областью определения гамма-функции Г(s) служит множество всех положительных чисел.

Интегрируя по частям (подстановка верхнего предела означает переход ),

. (2)

Формула , задаетфункциональное уравнение для гамма-функции.

Покажем, что при , где n-натуральное число,; т.е.гамма-функция есть обобщение понятия факториала. При

.

При , где n-натуральное число большее 1, пользуемся функциональным уравнением

.

Положив 0!=1, получим, что равенство выполняется для всех натуральных чисел.

Известно, что гамма-функция Эйлера бесконечно дифференцируема на , выпукла вниз и её минимум приходится в точке интервала, поскольку.