§4. Замена переменных в двойном интеграле

При вычислении интегралов часто бывает удобно сделать замену переменных , где– непрерывны в некоторой области. Впоследствии мы будем часто писать простовместои т.п. и, кроме того, говорить при выполнении вышеупомянутых условий, чтоx и y – непрерывно дифференцируемые в Δ функции. Будем также использовать обозначения

.

Пусть при этом формулы задают взаимно-однозначное отображение квадрируемых областей:. Кроме того, потребуем, чтобы всюду на областиΔ не равнялся 0 якобиан отображения .

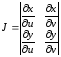Теорема 1.5. При сформулированных выше условиях для непрерывной на функциивыполняется равенство

.

►Строгое доказательство этой теоремы потребовало бы значительных усилий из-за обилия технических деталей. Мы изложим здесь схему доказательства. Во-первых, оба интеграла в формулировке теоремы существуют, поскольку – непрерывная функция.

Рассмотрим разбиение области Δ прямыми, параллельными осям u и v. Рассмотрим его часть, имеющую вид прямоугольника с вершинами

При отображении эти точки перейдут, соответственно, в точки

Далее, при

При малых производные, вычисленные в точках, мало отличаются от соответствующих производных, вычисленных в точке, поэтому и определённые выше векторымало отличаются от векторови, соответственно, и рассматриваемый четырёхугольник представляет собой «почти параллелограмм».

Как известно из курса линейной алгебры, площадь параллелограмма со сторонами

равна модулю определителя, составленного из координат этих векторов,

,

т.е равна . Поэтому при сделанном преобразовании координат интегральная сумма

близка по величине к интегральной сумме

.

Точнее говоря, можно доказать, что соответствующие интегральные суммы для интегралов, стоящих в правой и левой частях доказываемого равенства, отличаются друг от друга на стремящуюся к нулю величину. Поэтому и интегралы совпадают.◄

Замечание. Утверждение теоремы сохранится, если условие взаимной однозначности отображения нарушится на множестве нулевой площади.

§5. Переход к полярным координатам. Вычисление

Пусть требуется вычислить по области, которая задаётся в полярных координатах условиями

Сделаем замену переменных

При этой замене нарушается взаимная однозначность отображения. Точке (0,0) соответствует целый отрезок на оси. Однако и точка, и отрезок имеет нулевую площадь, и теорема, с учётом замечания, справедлива. Осталось вычислить якобиан преобразования.

Следовательно,

.

Полярные координаты бывают очень полезны при вычислениях. Рассмотрим пример.

Пример. Найти .

Решение. — это несобственный интеграл, и прежде всего следует установить его сходимость. По определению,

.

Первый из интегралов — собственный, второй — сходится по 1-й теореме о сравнении, так как при справедливо неравенство_,из которого следует, что, а интеграл , очевидно, сходится.

Обозначим (очевидно,). Тогда, поскольку обозначение переменной интегрирования можно выбрать произвольным, т.е.

,

имеем

,

где — квадрат, а— четверти круга, соответственно, радиусови. Так как, то по свойствам 2 , 3 двойного интеграла

.

В интеграле перейдем к полярным координатам:

.

Аналогично,

и .

При стремлении кполучаем, что

, то есть .