
- •Глава 1. Двойные интегралы
- •§1. Определение двойного интеграла и критерий интегрируемости
- •§2. Свойства двойных интегралов
- •3. Вычисление двойного интеграла сведением к повторному интегралу
- •§4. Замена переменных в двойном интеграле
- •§5. Переход к полярным координатам. Вычисление
- •Глава 2. Тройные интегралы
- •1.Гамма-функция
- •2. Бета-функция
- •3. Формула Стирлинга
§2. Свойства двойных интегралов
Свойство
1.
Если
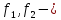 -
интегрируемые на квадрируемом множестве
-
интегрируемые на квадрируемом множестве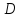 функции,
а
функции,
а
 числа, то
числа, то
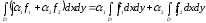 .
.
Иными словами, интеграл - линейный функционал.
Свойство
2.
Если
 - интегрируема на объединении квадрируемых
множеств
- интегрируема на объединении квадрируемых
множеств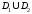 ,
то
,
то
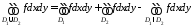 ,
,
причем
если площадь
пересечения
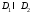 равна
0, то
равна
0, то
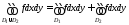 .
(Аддитивность интеграла по множеству).
.
(Аддитивность интеграла по множеству).
Свойство
3.
Если
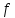 - интегрируемая на квадрируемом множестве
- интегрируемая на квадрируемом множестве
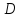 функция
и
функция
и
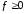 ,то
,то
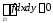 .
.
Свойство
4.
Если
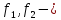 -
интегрируемые на квадрируемом множестве
-
интегрируемые на квадрируемом множестве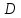 функции
и
функции
и
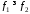 ,
то
,
то
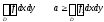 .
.
Свойство
5.
Если
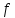 - интегрируемая на квадрируемом множестве
- интегрируемая на квадрируемом множестве
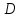 функция
,
причем
функция
,
причем
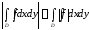 .
.
Свойство
6.
Если
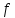 - интегрируемая на квадрируемом множестве
- интегрируемая на квадрируемом множестве
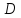 функция
, то функция
функция
, то функция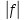 – также
интегрируемая,
причем
– также
интегрируемая,
причем
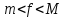 где
т,
М ограничивающие
множество значений функции
где
т,
М ограничивающие
множество значений функции
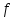 числа, то
выполняются
неравенства
числа, то
выполняются
неравенства
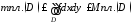 ,
,
т.е.
существует
число
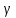 ,
удовлетворяющее неравенствам
,
удовлетворяющее неравенствам
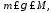 для
которого
для
которого
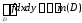 .
.
Если,
кроме того,
множество
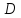 – связное*
и
– связное*
и
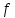 - непрерывна
на нём,
то
существует точка
- непрерывна
на нём,
то
существует точка
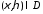 ,
для которой
,
для которой
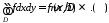 .
.
Доказывать эти свойства мы не будем, поскольку их доказательства вполне аналогичны доказательствам свойств обычного интеграла.
В
конце п.1.2. отмечено,
что если
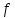 -непрерывная
на множестве
-непрерывная
на множестве
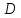 функция, то
функция, то
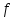 -
интегрируема
на
-
интегрируема
на
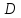 . Свойство
2 позволяет утверждать, что если
. Свойство
2 позволяет утверждать, что если
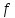 имеет разрывы на
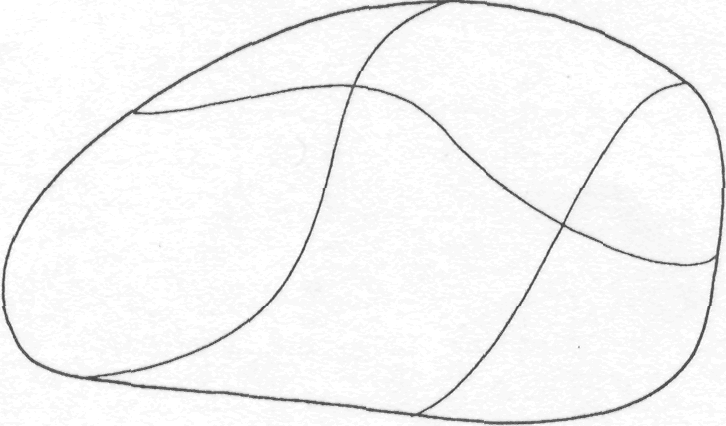
имеет разрывы на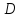 лишь
вдоль конечного числа спрямляемых
линий, разбивающих
лишь
вдоль конечного числа спрямляемых
линий, разбивающих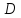 на
квадрируемые области, то
на
квадрируемые области, то
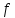 - интегрируема на
- интегрируема на
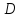 ,
т.к.,
по свойству 2, интеграл по
,
т.к.,
по свойству 2, интеграл по
 есть
просто сумма
конечного
числа интегралов по полученным частям
есть
просто сумма
конечного
числа интегралов по полученным частям (на которых
(на которых непрерывна и, значит, интегрируема).
непрерывна и, значит, интегрируема).
*Примечание. Связным множеством на плоскости назовем такое множество, любые две точки которого можно соединить кусочно-гладкой кривой, лежащей в этом множестве.
3. Вычисление двойного интеграла сведением к повторному интегралу
Двойной
интеграл – новый объект и мы укажем
способ его вычисления сведением к
повторному вычислению определённого
интеграла. Сначала рассмотрим двойной
интеграл по прямоугольной области
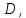 стороны которой параллельны осям
координат.
стороны которой параллельны осям
координат.
Теорема
1.3.
Пусть
для функции
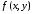 существует двойной интеграл
существует двойной интеграл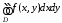 по
области
по
области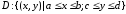 .
Кроме того, пусть для любого
.
Кроме того, пусть для любого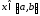 существует
существует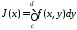 .
.
Тогда существует и интеграл, называемый повторным:

и выполняется равенство
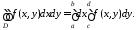 (2)
(2)
►Разобьём
прямоугольник
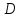 на прямоугольники, обозначенные
на прямоугольники, обозначенные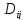 ,
прямыми, проходящими параллельно оси
,
прямыми, проходящими параллельно оси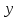 через
точки
через
точки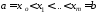 и прямыми, параллельными оси
и прямыми, параллельными оси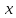 и проходящими через точки
и проходящими через точки Таким образом,
Таким образом,
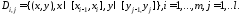
Пусть
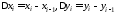 ,
числа
,
числа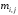 и
и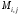 ,
соответственно, равны нижней и верхней
граням функции
,
соответственно, равны нижней и верхней
граням функции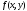 на
на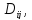 откуда
откуда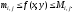 Проинтегрируем эти неравенства по
Проинтегрируем эти неравенства по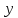 на
отрезках
на
отрезках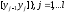 :
:
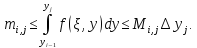
Суммируя
эти неравенства по
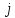 от
от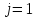 до
до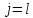 ,
получаем
,
получаем
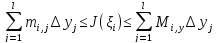
Умножим
все части этих неравенств на
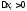 и суммируем полученные неравенства по
и суммируем полученные неравенства по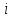 от
от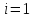 до
до :
:
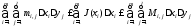 .
.
Поскольку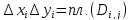 ,
эти неравенства можно переписать в виде
,
эти неравенства можно переписать в виде
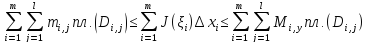
или
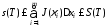 ,
,
где
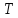 – разбиение
– разбиение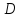 на прямоугольники
на прямоугольники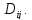 При
При стремится к нулю и величина
стремится к нулю и величина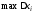 .
Кроме того, при
.
Кроме того, при также
также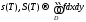 .
Значит, интеграл
.
Значит, интеграл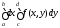 существует и равен
существует и равен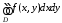 ,
что и утверждалось.
◄
,
что и утверждалось.
◄
Замечания.
В случае, когда
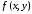 непрерывна
на
непрерывна
на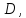 все
условия теоремы выполняются и равенство
(2) справедливо.
все
условия теоремы выполняются и равенство
(2) справедливо.Отметим, что интеграл
 представляет собой собственный интеграл,
зависящий от параметра.
представляет собой собственный интеграл,
зависящий от параметра.
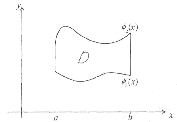
Рассмотрим случай криволинейной трапеции. Справедлива такая теорема:
Теорема
1.4 (Фубини).
Пусть
область
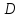 задана неравенствами
задана неравенствами
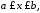
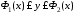 ,
где
,
где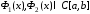 .
Пусть существует
.
Пусть существует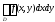 и для любого
и для любого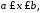 существует
существует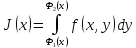 .
Тогда существует интеграл
.
Тогда существует интеграл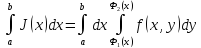 и он равен
и он равен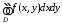 .
.
►Так
как
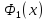 непрерывна на
непрерывна на ,
существует её минимальное значение
,
существует её минимальное значение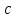 на
этом отрезке. Аналогично, существует
максимальное значение
на
этом отрезке. Аналогично, существует
максимальное значение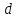 функции
функции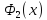 на отрезке
на отрезке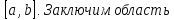
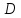 в прямоугольник
в прямоугольник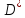 ,
состоящий из точек
,
состоящий из точек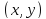 ,
,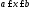 ,
, .
На этом прямоугольнике рассмотрим
функцию
.
На этом прямоугольнике рассмотрим
функцию
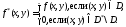
Условия
предыдущей теоремы для функции
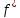 выполнены. Она интегрируема в
выполнены. Она интегрируема в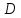 ,
равна 0 (и, значит, интегрируема) в
,
равна 0 (и, значит, интегрируема) в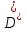 .
Следовательно, она интегрируема на всём
множестве
.
Следовательно, она интегрируема на всём
множестве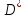 .
При этом
.
При этом
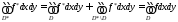 .
.
Наконец,
для любого
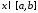 выполнено
равенство
выполнено
равенство
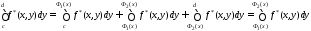 .
.
По доказанному в предыдущей теореме,
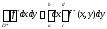 ,
,
откуда сразу получаем:
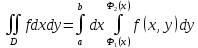 ,
,
что и требовалось доказать.◄
Следствие:
Пусть
 )
непрерывна
в области
)
непрерывна
в области
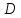 ,
ограниченной
сверху графиком функции
,
ограниченной
сверху графиком функции
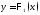 ,
снизу
-
,
снизу
-
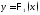 ,
где
,
где
 ,
a
по
бокам - отрезками вертикальных прямых
х
= а
и
х
= b.
Тогда
,
a
по
бокам - отрезками вертикальных прямых
х
= а
и
х
= b.
Тогда
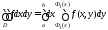 .
.
►Из
непрерывности
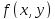 сразу следует её интегрируемость на
сразу следует её интегрируемость на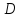 .
Кроме того, для любого
.
Кроме того, для любого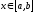 функция
функция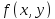 непрерывна (а, значит, интегрируема поу).
Все условия теоремы выполнены.
◄
непрерывна (а, значит, интегрируема поу).
Все условия теоремы выполнены.
◄
Замечание.
Если область
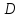 можно ограничить так:
можно ограничить так: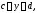
 ,
,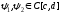 ,
то
,
то
 .
.
Смысл этих теорем ясен – указан способ сведения двойного интеграла к собственным интегралам, зависящим от параметра.
