
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации
Предмет:
Файл:Глава 15.doc
X
- •Глава 15. Определённый интеграл
- •§15.1.Понятие площади плоской фигуры. Задача о вычислении площади криволинейной трапеции
- •15.1.1. Площадь многоугольника
- •§15.2. Определение интеграла и необходимое условие его существования
- •15.2.1Разбиение отрезка. Интегральные суммы. Определение интеграла (по Риману)
- •15.2.2.Необходимое условие интегрируемости функции
- •§15.3. Критерий интегрируемости
- •15.3.1. Определение сумм Дарбу
- •15.3.2. Свойства сумм Дарбу
- •§15.4. Критерий интегрируемости функции. Классы интегрируемых функций
- •15.4.1. Критерий интегрируемости функции
- •15.4.2. Интегрируемость монотонной функции. Интегрируемость непрерывной функции
- •§15.5. Свойства определённого интеграла
- •Тогда объединение разбиений иобразует некоторое размеченное разбиениеотрезкас, для которого справедлива формула. Поэтому, с учетом неравенств (18)(20), имеем оценки
- •§15.6. Теоремы о среднем значении
- •§15.7. Определённый интеграл с переменным верхним пределом
- •§15.8. Основная формула интегрального исчисления (Формула Ньютона-Лейбница)
- •15.8.1. Основная формула интегрального исчисления
- •15.8.2. Замена переменной и интегрирование по частям в определённом интеграле.
15.8.2. Замена переменной и интегрирование по частям в определённом интеграле.
Теорема15.22.
(Замена
переменной)
Пусть
![]() и
и ![]() ,
где
,
где ![]() определена и непрерывна на
определена и непрерывна на ![]() ;
;
значения ![]() при
при ![]() не выходят за пределы отрезка
не выходят за пределы отрезка ![]() ;
;
![]() ;
;![]() .
.
Тогда 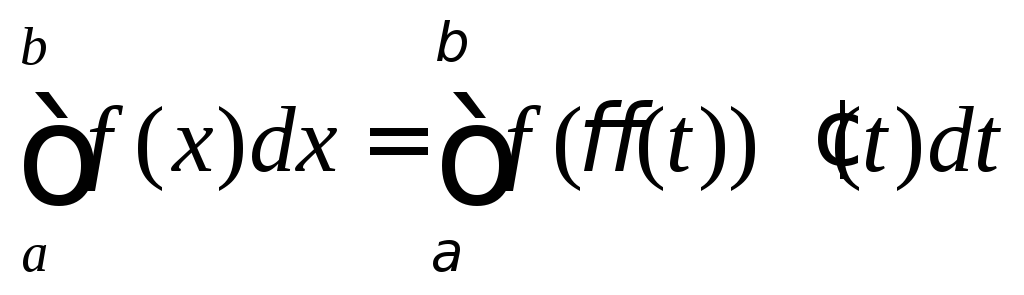 . (28)
. (28)
►Пусть ![]() — первообразная для
— первообразная для ![]() .
Тогда
.
Тогда ![]() .
Поэтому выполняются равенства:
.
Поэтому выполняются равенства: ![]() ,
,![]() и требуемое равенство (28) установлено.◄
и требуемое равенство (28) установлено.◄
Теорема 15.23.
(Интегрирование
по частям).
Пусть ![]() .
.
Тогда ![]()
![]()
►
![]() .
Поскольку
.
Поскольку ![]() — непрерывная функция, то существует
её первообразная
— непрерывная функция, то существует
её первообразная ![]() ,
т.е.
,
т.е. ![]() .
Тогда
.
Тогда ![]()
![]() и
и
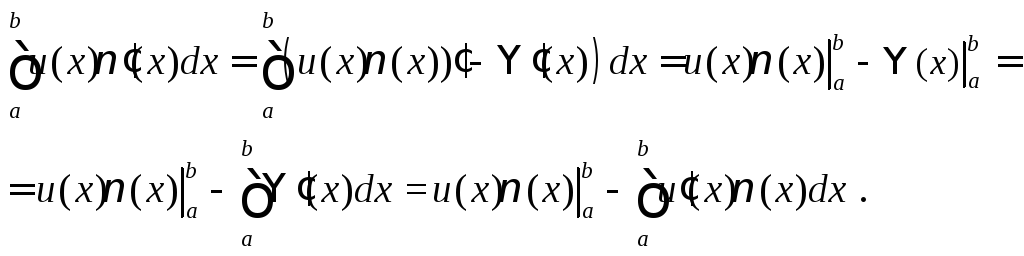
Теорема доказана.◄
Пример.
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
