
- •Глава 15. Определённый интеграл
- •§15.1.Понятие площади плоской фигуры. Задача о вычислении площади криволинейной трапеции
- •15.1.1. Площадь многоугольника
- •§15.2. Определение интеграла и необходимое условие его существования
- •15.2.1Разбиение отрезка. Интегральные суммы. Определение интеграла (по Риману)
- •15.2.2.Необходимое условие интегрируемости функции
- •§15.3. Критерий интегрируемости
- •15.3.1. Определение сумм Дарбу
- •15.3.2. Свойства сумм Дарбу
- •§15.4. Критерий интегрируемости функции. Классы интегрируемых функций
- •15.4.1. Критерий интегрируемости функции
- •15.4.2. Интегрируемость монотонной функции. Интегрируемость непрерывной функции
- •§15.5. Свойства определённого интеграла
- •Тогда объединение разбиений иобразует некоторое размеченное разбиениеотрезкас, для которого справедлива формула. Поэтому, с учетом неравенств (18)(20), имеем оценки
- •§15.6. Теоремы о среднем значении
- •§15.7. Определённый интеграл с переменным верхним пределом
- •§15.8. Основная формула интегрального исчисления (Формула Ньютона-Лейбница)
- •15.8.1. Основная формула интегрального исчисления
- •15.8.2. Замена переменной и интегрирование по частям в определённом интеграле.
§15.6. Теоремы о среднем значении
Теорема 15.17.
(Теорема о среднем значении).
Пусть
![]() интегрируема на
интегрируема на
![]() .
Пусть при
.
Пусть при
![]() выполнены
неравенства
выполнены
неравенства
![]() .
Тогда
.
Тогда
Тогда существует
число
![]() ,
удовлетворяющее неравенствам
,
удовлетворяющее неравенствам
![]() такое, что
такое, что
![]() .
.
Если, кроме того,
![]() ,
то существует
,
то существует
![]() такое, что
такое, что
![]() .
т. е.
.
т. е.
![]() .
.
► Из теоремы 15.15
и того, что для любой постоянной ![]() выполнено равенство
выполнено равенство ![]() ,
следуют неравенства
,
следуют неравенства
![]() .
.
Из них сразу получаем, что
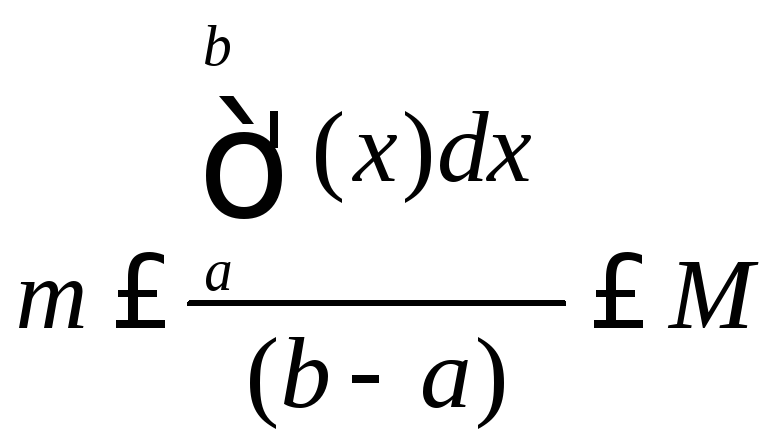 .
.
Обозначив 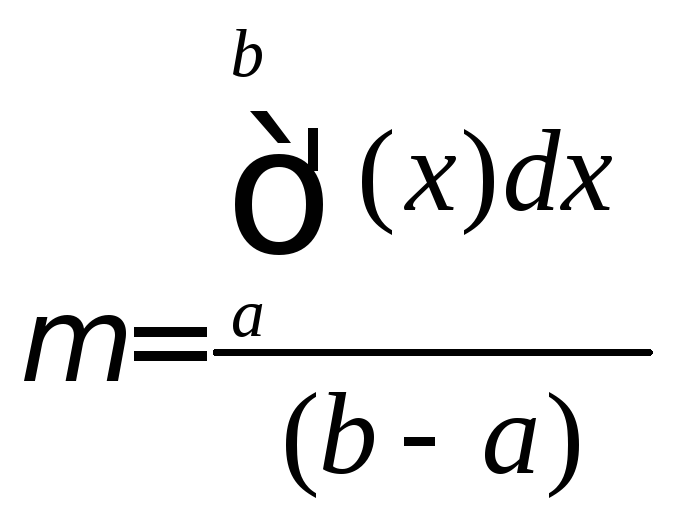 ,
получаем требуемое утверждение.
,
получаем требуемое утверждение.
Если же ![]() ,
то она принимает все свои промежуточные
значения между своими наименьшим
,
то она принимает все свои промежуточные
значения между своими наименьшим ![]() и наибольшим
и наибольшим ![]() значениями
на отрезке
значениями
на отрезке ![]() .
.
При этом, по доказанному,
![]() ,
,![]() .
.
Как отмечено выше,
число
![]() является значением
функции
является значением
функции ![]() ,т.е.
,т.е.
![]() и
и
![]() .◄
.◄
Теорема. 15.18.(Обобщённая теорема о среднем значении). Пусть:
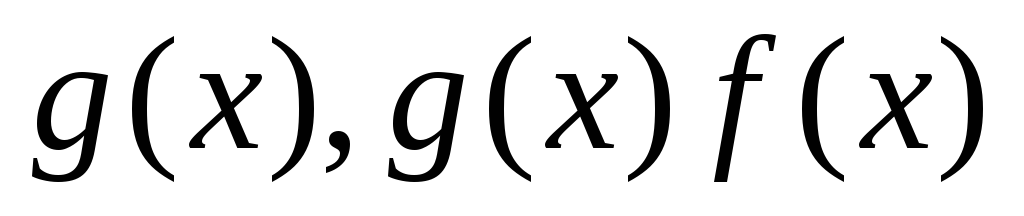 –интегрируемы
на
–интегрируемы
на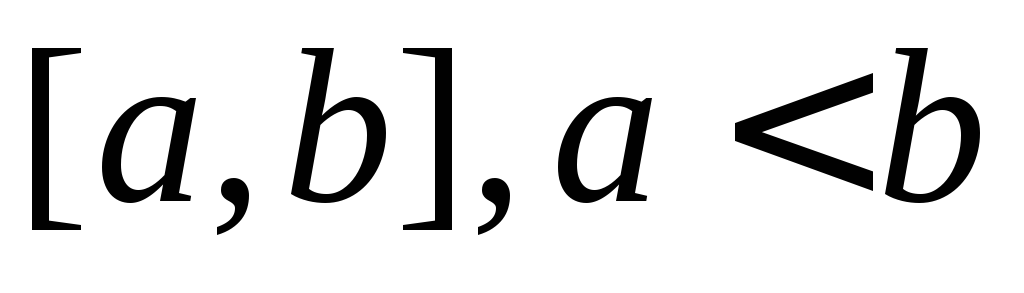 ;
; ;
;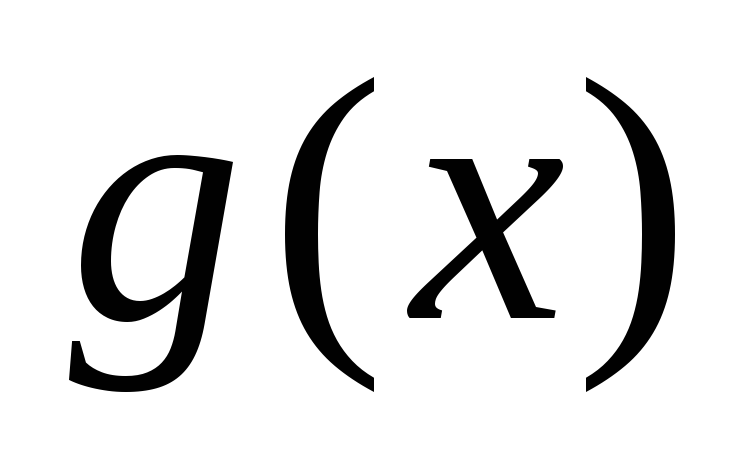 не меняет знак
на
не меняет знак
на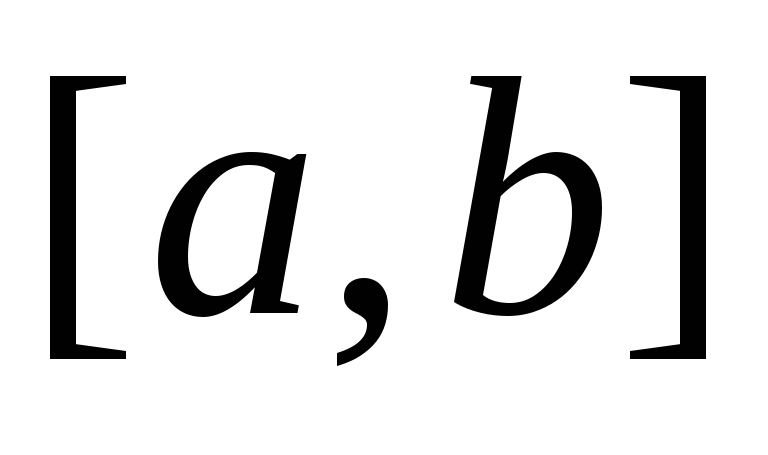 .
.
Тогда существует
![]() ,
удовлетворяющее неравенствам
,
удовлетворяющее неравенствам
![]() такое, что
такое, что
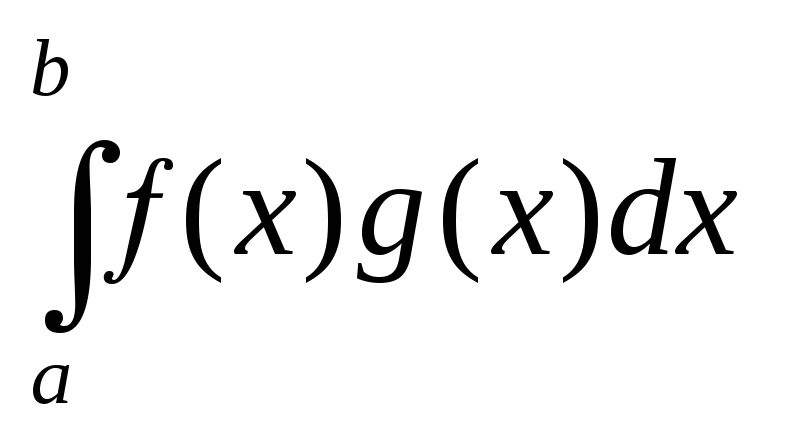 =
=
![]() .
.
Если, при этом,
![]() ,
то существует
,
то существует
![]() такое, что
такое, что
![]() .
.
►Пусть, для
определенности, ![]() на
на
![]() .
.
Тогда ![]() и
и
![]()
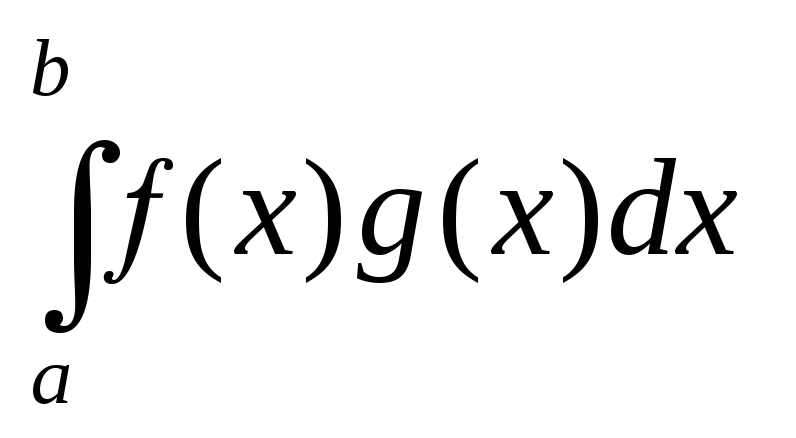
![]() . (26)
. (26)
По теореме 15.14,

0. Если оказалось, что
0. Если оказалось, что ![]() ,
то из (26) следует, что
=0 и теорема
справедлива при любом значении
,
то из (26) следует, что
=0 и теорема
справедлива при любом значении
![]() .
Если же
.
Если же ![]() ,то разделив на это
число все части неравенств (26), получим,
что
,то разделив на это
число все части неравенств (26), получим,
что
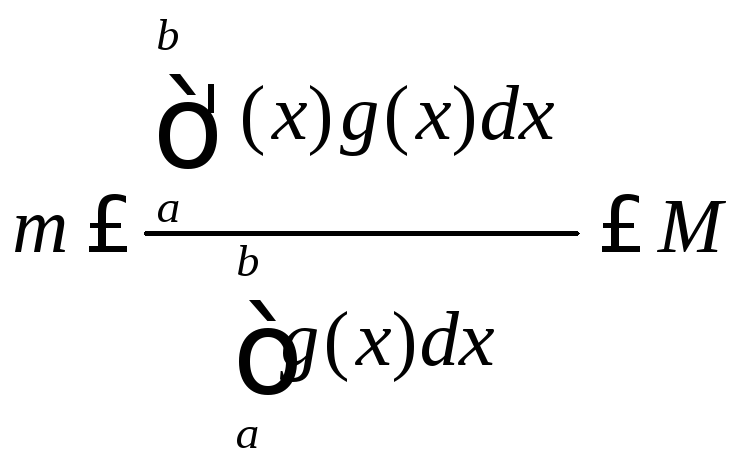 ,
,
откуда, при 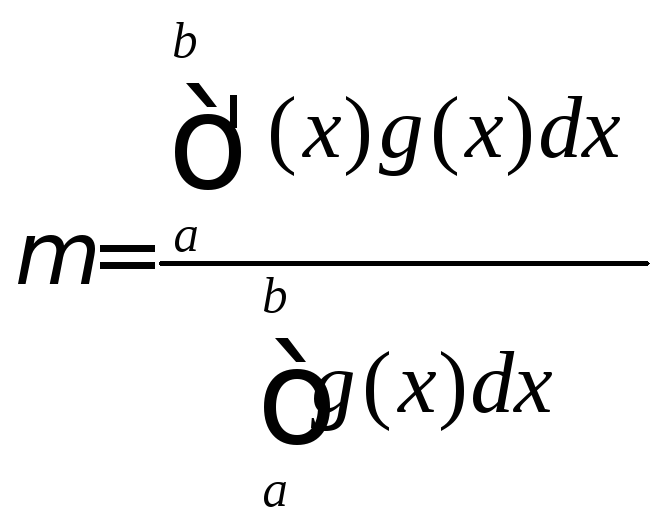 получаем утверждение теоремы.
Если, при
этом,
получаем утверждение теоремы.
Если, при
этом,![]() ,
то, как и в теореме 15.17, существует
,
то, как и в теореме 15.17, существует![]() такое, что
такое, что![]() .
◄
.
◄
§15.7. Определённый интеграл с переменным верхним пределом
Пусть
![]() интегрируема на
интегрируема на![]() .
Тогда, по свойству аддитивности интеграла,
.
Тогда, по свойству аддитивности интеграла,![]() интегрируема на
интегрируема на![]() при любом
при любом![]() .
.
Определение. Рассмотрим функцию
![]() (27)
(27)
Эта функция называется определённым интегралом с переменным верхним пределом.
Теорема 15.19.
Если
![]() – интегрируема на
– интегрируема на![]() ,
то
,
то![]() .
.
► Достаточно
доказать, что при
![]() приращение
приращение![]() (при этом предполагается, что
(при этом предполагается, что![]() ).
По определению (27)
).
По определению (27)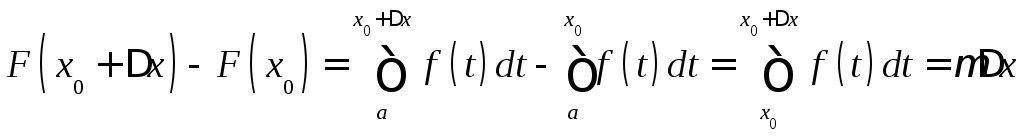 ,
,
согласно теореме
о среднем (при этом
![]() ,
где
,
где![]() ,
,![]() ).
При
).
При![]() очевидно,
очевидно,![]() и теорема доказана.◄
и теорема доказана.◄
Теорема 15.20.
Пусть
![]() интегрируема на
интегрируема на![]() и
непрерывна в точке
и
непрерывна в точке![]() .
Тогда
.
Тогда![]() имеет производную в точке
имеет производную в точке![]() ,
причём
,
причём![]() .
.
►
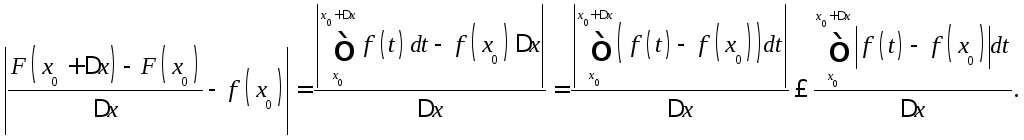 По
условию,
По
условию,
![]() непрерывна в точке
непрерывна в точке![]() ,
следовательно,
,
следовательно,![]() ,
,
как только
![]() .
Но
.
Но![]() .
Значит, при
.
Значит, при![]()
![]() ,
,
что как раз и
означает, что
![]() .◄
.◄
Определение.
Если для всех
![]() справедливо равенство
справедливо равенство![]() ,
то
,
то
![]() называетсяпервообразной
функцией для
функции
называетсяпервообразной
функцией для
функции![]() на
на![]() .
.
Можно рассматривать
первообразную
и на отрезке
![]() ,
тогда в точке
,
тогда в точке![]() должно выполнятся равенство
должно выполнятся равенство![]() ,
а в точке
,
а в точке![]() – равенство
– равенство![]() .
.
Следствие. Если![]() , то
, то![]() (т.е.
(т.е.![]() –первообразная
для
–первообразная
для
![]() ).
Иными словами, непрерывная функция
имеет первообразную.
).
Иными словами, непрерывная функция
имеет первообразную.
Замечание. Дадим графическую интерпретацию теоремы.
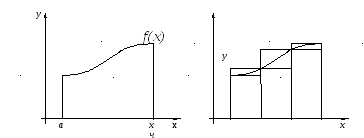
Площадь под графиком
равна
![]() ,
а производная
,
а производная![]() равна
равна
![]() .
.
Замечание. Что
будет, если функция
![]() не непрерывна?
Пример
не непрерывна?
Пример
![]() ,
,![]()
показывает, что ![]() (т. к.
(т. к.
![]() ),
т.е.
),
т.е.![]() ,
,
поэтому в случае
точки разрыва утверждение теоремы может
оказаться неверным. В этом случае
производная
функции
![]() существует,
но не равна
существует,
но не равна
![]() .
.
Рассмотрим ещё пример
![]()
В этом случае
производная
функции
![]() в
точке
в
точке ![]() не существует, однако существуют
не существует, однако существуют ![]()
§15.8. Основная формула интегрального исчисления (Формула Ньютона-Лейбница)
15.8.1. Основная формула интегрального исчисления
Теорема15.21.
(Формула Ньютона-Лейбница). Если
![]() ,
то для любой первообразной
,
то для любой первообразной![]() имеет место равенство
имеет место равенство![]() .
.
►По следствию
теоремы 15.20, первообразная
![]() существует. Если
существует. Если![]() – любая другая первообразная, то
существует
– любая другая первообразная, то
существует![]() такая, что
такая, что![]() , т.е.
, т.е.![]() . Тогда
. Тогда![]() ,
что и требовалось доказать.◄
,
что и требовалось доказать.◄
Замечание.
Разность ![]() часто обозначают
часто обозначают
![]() .
.
