15.4.2. Интегрируемость монотонной функции. Интегрируемость непрерывной функции

Следствием доказанного критерия 15.5.является интегрируемость монотонной функции.

Теорема 15.6. Если не убывает (не возрастает) на, то она интегрируема на.

► Пусть не убывает. Тогда на отрезкевыполняются

равенства: ,. Если, то- постоянная и ее

интегрируемость очевидна (). Если, то положим

.

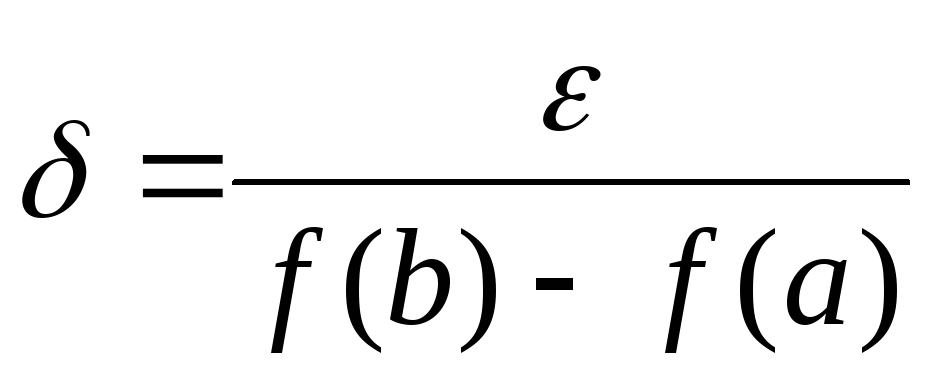Тогда если , то

◄

Докажем теорему, которая будет очень часто использоваться.

Теорема 15.7. . Если , то — интегрируема на .

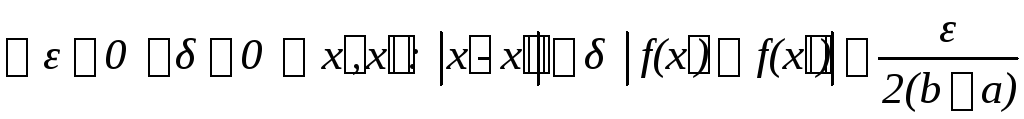► По теореме Кантора, равномерно непрерывна на , т.е. (10).

Рассмотрим разбиение отрезка с диаметром меньшим, чем выбранное . Тогда на каждом отрезке имеет место неравенство:

(11).

Действительно, достаточно подобрать точку так, что

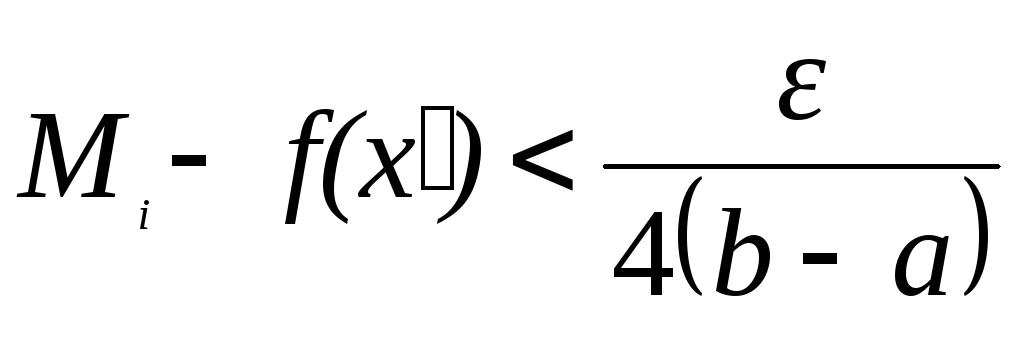(12)

и точку так, чтобы

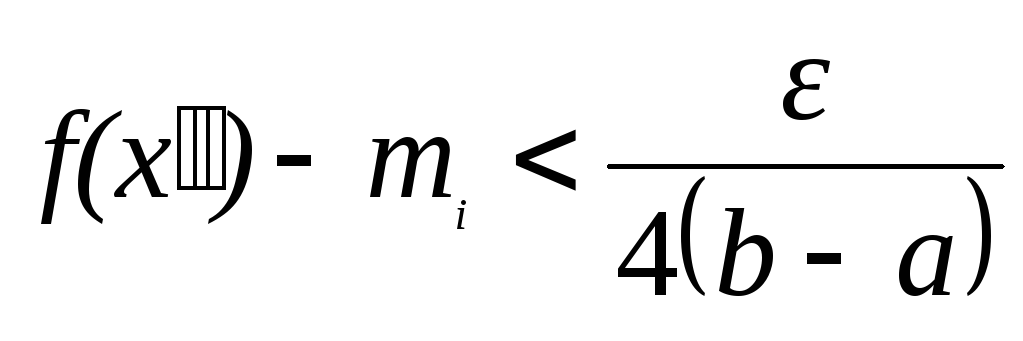(13).

(Это можно сделать, т.к. числа — точные грани множества значений).

Тогда ввиду (10), (12), (13) , и

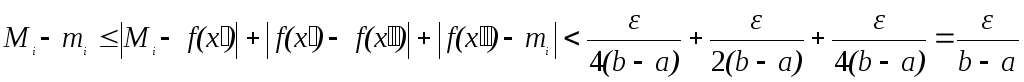. Неравенство (11) доказано. Тогда

.

То есть критерий интегрируемости выполняется.◄

Ещё раз вернёмся к задаче о площади криволинейной трапеции.

Теорема 15.8. Пусть — фигура, ограниченная снизу осью, по бокам — отрезками вертикальных прямыхи,, а сверху — графиком непрерывной на отрезкефункции(см. рис.1). Тогдаимеет площадь, причем

=

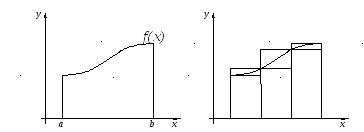
Рис. 1. Рис. 2.

►Для произвольного разбиения отрезканижняя сумма Дарбупредставляет собой площадь многоугольника,, а верхняя сумма Дарбу — площадь многоугольника,(рис. 2). Так какнепрерывна на, она интегрируема на этом отрезке и для любогосуществуеттакое, что для всех разбиенийс диаметромимеет место неравенство. Значит, для любогосуществуют многоугольникитакие, что. Это означает квадрируемость . Наконец, площадьравна и . Эти равенства означают, что

.◄

Следствие. Пусть и— непрерывные нафункции, причем для всехвыполняется неравенство. Тогда площадь криволинейной трапеции, ограниченной сверху графиком функции, снизу — графиком функции, а по бокам — отрезками вертикальных прямыхиравна

.

►Так как интегрируемые функции ограничены, существует постоянная такая, что. Площадь между графиками функций и такая же, как площадь между графиками функций. Для доказательства следствия достаточно применить к этим функциям теорему 15.8, заметить, что искомая площадь равна разности площадей

и применить теорему 15.13 из следующего параграфа, согласно которой

◄

Теорема 15.9 . Если функция ограничена на отрезкеи имеет на нем конечное число точек разрыва, то она интегрируема на этом отрезке.

►Ограничимся схемой доказательства.

Для любого разбиения отрезкаполученные отрезки либо содержат точку разрыва, либо не содержат. Количество отрезков, куда может входить точка разрыва, не превосходит удвоенного числа точек разрыва, так как точка разрыва может принадлежать одному отрезку (когда она не совпадает с точкой деления), либо двум отрезкам (когда она совпадает с точкой деления). По условию, функция ограничена, поэтому существуют точная нижняя граньи точная верхняя граньмножества её значений. Следовательно, колебаниена любом отрезке, содержащем точку разрыва, не превосходит.

Таким образом, для любого можно выбратьстоль малым, чтобы сумма величиндля отрезков, содержащих точки разрыва, стала меньше.

Так же, как при доказательстве теоремы об интегрируемости непрерывной функции, можно доказать, что сумма величин для отрезков, не содержащих точек разрыва, меньше, чем, при достаточно малых значениях.

Но это означает, что при достаточно малых вся сумма

и теорема доказана.◄