
- •Глава 15. Определённый интеграл
- •§15.1.Понятие площади плоской фигуры. Задача о вычислении площади криволинейной трапеции
- •15.1.1. Площадь многоугольника
- •§15.2. Определение интеграла и необходимое условие его существования
- •15.2.1Разбиение отрезка. Интегральные суммы. Определение интеграла (по Риману)
- •15.2.2.Необходимое условие интегрируемости функции
- •§15.3. Критерий интегрируемости
- •15.3.1. Определение сумм Дарбу
- •15.3.2. Свойства сумм Дарбу
- •§15.4. Критерий интегрируемости функции. Классы интегрируемых функций
- •15.4.1. Критерий интегрируемости функции
- •15.4.2. Интегрируемость монотонной функции. Интегрируемость непрерывной функции
- •§15.5. Свойства определённого интеграла
- •Тогда объединение разбиений иобразует некоторое размеченное разбиениеотрезкас, для которого справедлива формула. Поэтому, с учетом неравенств (18)(20), имеем оценки
- •§15.6. Теоремы о среднем значении
- •§15.7. Определённый интеграл с переменным верхним пределом
- •§15.8. Основная формула интегрального исчисления (Формула Ньютона-Лейбница)
- •15.8.1. Основная формула интегрального исчисления
- •15.8.2. Замена переменной и интегрирование по частям в определённом интеграле.
§15.2. Определение интеграла и необходимое условие его существования
15.2.1Разбиение отрезка. Интегральные суммы. Определение интеграла (по Риману)
Определение.
Точки
![]() задаютразбиение
отрезка
задаютразбиение
отрезка
![]() .
Для краткости будем обозначать разбиение
буквой
.
Для краткости будем обозначать разбиение
буквой![]() .
.
О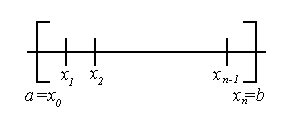 бозначим
бозначим![]()
Определение.
Наибольшее из чисел
![]() называетсядиаметром
разбиения
называетсядиаметром
разбиения
![]() и обозначается
и обозначается![]()
Определение.
Если произвольным образом выбрать точки
![]() то получитсяразбиение
то получитсяразбиение
![]() с отмеченными точками
с отмеченными точками![]()
Иногда, для
краткости, будем обозначать набор точек
![]() символом
символом![]()
Перейдем к основным определениям.
Определение.
Пусть функция
![]() определена на отрезке
определена на отрезке![]() ,
и пусть задано разбиение
,
и пусть задано разбиение![]() этого отрезка с отмеченными точками
этого отрезка с отмеченными точками![]() Интегральной
суммой
называется величина
Интегральной
суммой
называется величина
![]() .
.
Для обозначения
интегральной суммы будем использовать
символ
![]() ,
или просто
,
или просто![]() .
.
Д
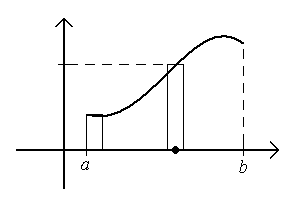
![]()
![]()
![]() интегральная сумма
интегральная сумма![]() представляет собой просто площадь
ступенчатого многоугольника, составленного
из прямоугольников с основаниями
представляет собой просто площадь
ступенчатого многоугольника, составленного
из прямоугольников с основаниями![]() ,
имеющих высоты, равные
,
имеющих высоты, равные![]() .
.
Определение.
Пусть существует число
![]() такое, что для любого
такое, что для любого![]() существует число
существует число![]() такое, что для любого разбиения
такое, что для любого разбиения![]() отрезка
отрезка![]() ,
удовлетворяющего условию
,
удовлетворяющего условию![]() ,
и для любого выбора точек
,
и для любого выбора точек![]() выполняется неравенство
выполняется неравенство![]()
Тогда функция
![]() называетсяинтегрируемой
(по Риману) на отрезке
называетсяинтегрируемой
(по Риману) на отрезке
![]() ,(что
часто обозначают так:
,(что
часто обозначают так:![]() )
а число
)
а число
![]() называется ееинтегралом
по отрезку
называется ееинтегралом
по отрезку
![]() .
Интеграл обозначается символом
.
Интеграл обозначается символом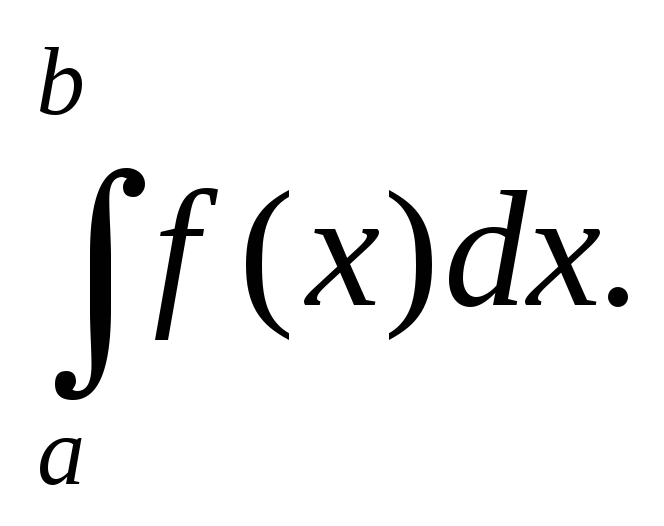
15.2.2.Необходимое условие интегрируемости функции
Теорема 15.2.
Если функция
![]() интегрируема на отрезке
интегрируема на отрезке![]() ,
то она ограничена на
,
то она ограничена на![]() .
.
►Возьмем в
определении интеграла
![]() = 1 и рассмотрим соответствующее ему
= 1 и рассмотрим соответствующее ему![]() .
Пусть
.
Пусть![]() –
любое разбиение, удовлетворяющее условию
–
любое разбиение, удовлетворяющее условию
![]() .
.
Для того, чтобы
убедиться в справедливости теоремы,
достаточно доказать, что при всех
![]() ,
,![]() = 1,…,
= 1,…,![]() функция
функция
![]() ограничена на отрезке
ограничена на отрезке![]() ,
т.е.
,
т.е.![]() .
Действительно, тогда для
.
Действительно, тогда для
![]() имеем при
имеем при
![]() :
:
![]() ,
т.к.
,
т.к.![]() входит в некоторый отрезок
входит в некоторый отрезок![]() и, значит |
и, значит |![]() .
.
Выберем любое
![]() ,
,
![]() = 1,…,
= 1,…,![]() и представим интегральную сумму
и представим интегральную сумму
![]() в виде
в виде
![]() (1)
(1)
Зафиксируем
произвольным образом числа![]() ,…,
,…,![]() ,
,![]() ,…,
,…,![]() выбранные в соответствующих промежутках.
При этом первое и третье слагаемые в
равенстве (1) примут определенное
фиксированное значение. Обозначим сумму
этих слагаемых буквойK.
Таким образом, при любом
выбранные в соответствующих промежутках.
При этом первое и третье слагаемые в
равенстве (1) примут определенное
фиксированное значение. Обозначим сумму
этих слагаемых буквойK.
Таким образом, при любом
![]()
![]() (2)
(2)
По условию, функция
интегрируема, значит |![]() |<1,
т.е. –1<
|<1,
т.е. –1<![]() <1,
или
<1,
или![]()
![]()
![]() .
.
Откуда, учитывая (2),
![]() ,
,
![]() ,
,
![]() (3)
(3)
Левая и правая
части неравенств (3) представляют собой
величины, не зависящие от
![]() .
Поэтому
неравенства (3) означают, что
.
Поэтому
неравенства (3) означают, что 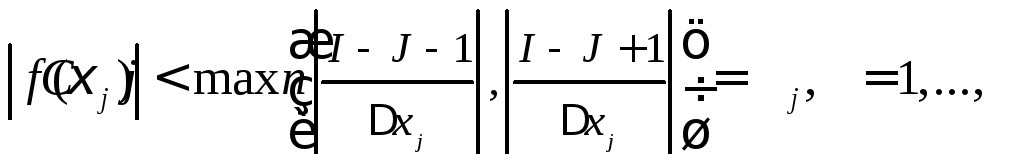 .
Теорема доказана.◄
.
Теорема доказана.◄
§15.3. Критерий интегрируемости
15.3.1. Определение сумм Дарбу
При исследовании вопроса о существовании интеграла важную роль играют так называемые суммы Дарбу (Г. Дарбу (18421917)).
По доказанной
теореме 15.2 функция
![]() ограничена на
ограничена на![]() и, следовательно, для любого разбиения
и, следовательно, для любого разбиения![]() отрезка она ограничена на всех отрезках
отрезка она ограничена на всех отрезках![]() (т.е. множество её значений на этом
отрезке ограничено сверху и снизу).
Обозначим
(т.е. множество её значений на этом
отрезке ограничено сверху и снизу).
Обозначим
![]()
точную верхнюю грань, а
точную верхнюю грань, а
![]()
точную нижнюю грань множества значений
функции
точную нижнюю грань множества значений
функции
![]() на
на![]()
Определение.
Числа ![]() и
и ![]() называются, соответственно, верхней
и
нижней суммами Дарбу
функции
называются, соответственно, верхней
и
нижней суммами Дарбу
функции
![]() для разбиения
для разбиения![]() на отрезке
на отрезке![]() .
.
Теорема
15.3.
Верхняя сумма
Дарбу
![]() представляет собой точную верхнюю
грань, а нижняя сумма Дарбу
представляет собой точную верхнюю
грань, а нижняя сумма Дарбу![]()
точную нижнюю грань множества значений
интегральных сумм при заданном разбиении
точную нижнюю грань множества значений
интегральных сумм при заданном разбиении
![]() и всевозможных выборах точек
и всевозможных выборах точек![]() .
.
►Проведем его для верхней суммы Дарбу. Для нижней суммы рассуждения вполне аналогичные.
Во-первых, для
любого ![]() и для любой точки
и для любой точки ![]() имеет место неравенство
имеет место неравенство
![]() (по определению
(по определению![]() ).
Значит,
).
Значит,
![]() ,
,
![]() . (4)
. (4)
Суммируя неравенства
(4) по всем ![]() получаем
получаем
![]() .
.
Таким образом,![]() — верхняя грань множества
— верхняя грань множества![]() по всевозможным выборам
по всевозможным выборам![]() .
.
Осталось доказать,
что
![]() — точная верхняя грань этого множества.
Для этого возьмем произвольное
— точная верхняя грань этого множества.
Для этого возьмем произвольное![]() Поскольку
Поскольку![]() — точная верхняя грань множества
значений
— точная верхняя грань множества
значений![]() на отрезке
на отрезке![]() ,
,
![]() ,
существует точка
,
существует точка ![]() такая, что
такая, что
![]() ,
,![]() и
и
![]() ,
,
![]() . (5)
. (5)
Суммируя неравенства
(5) по ![]() получаем,
что
получаем,
что
![]() ,
,
т.к. ![]() (суммарная длина отрезков, составляющих
отрезок
(суммарная длина отрезков, составляющих
отрезок
![]() ,
равна длине этого отрезка).
,
равна длине этого отрезка).
Итак, доказано,
что для любого
![]() можно так выбрать точки
можно так выбрать точки![]() ,
что
,
что![]() ,
что как раз и означает, что
,
что как раз и означает, что![]() ,
где верхняя грань взята по всевозможным
выборам точек
,
где верхняя грань взята по всевозможным
выборам точек
![]() .
Теорема доказана.◄
.
Теорема доказана.◄
Замечание.
Очевидны неравенства:
![]() .
.
Дадим графическую иллюстрацию введённых понятий.
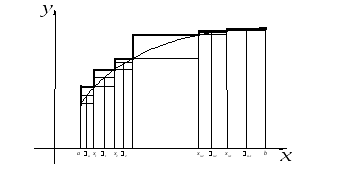
Заметим, что нижняя
сумма Дарбу, соответствующая разбиению
![]() ,
представляет собой площадь многоугольника,
верхняя граница которого на рисунке
есть нижняя из 3 ломаных, отмечена жирной
линией.
,
представляет собой площадь многоугольника,
верхняя граница которого на рисунке
есть нижняя из 3 ломаных, отмечена жирной
линией.
Верхняя сумма Дарбу — это площадь многоугольника, верхняя граница которого — верхняя из 3 ломаных линий, отмечена еще более жирной линией.
Наконец, интегральная
сумма, соответствующая выбору точек
![]() — это площадь многоугольника, верхняя
граница которого на рисунке заключена
между описанными выше линиями и
изображена простой линией.
— это площадь многоугольника, верхняя
граница которого на рисунке заключена
между описанными выше линиями и
изображена простой линией.
