
Производная ф-ции Правила дифференцирования
.docПроизводная ф-ции/ Правила дифференцирования
Производной функции у= f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если предел существует)
Нахождение производной функции называется дифференцированием этой функции.
Геометрический смысл производной: производная f’(x0) = угловой коэффициент (тангенс угла наклона) касательной.
Правила дифференцирования.
-
Производная постоянной равна нулю;
-
Производная аргумента равна 1
-
Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций:

-
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:
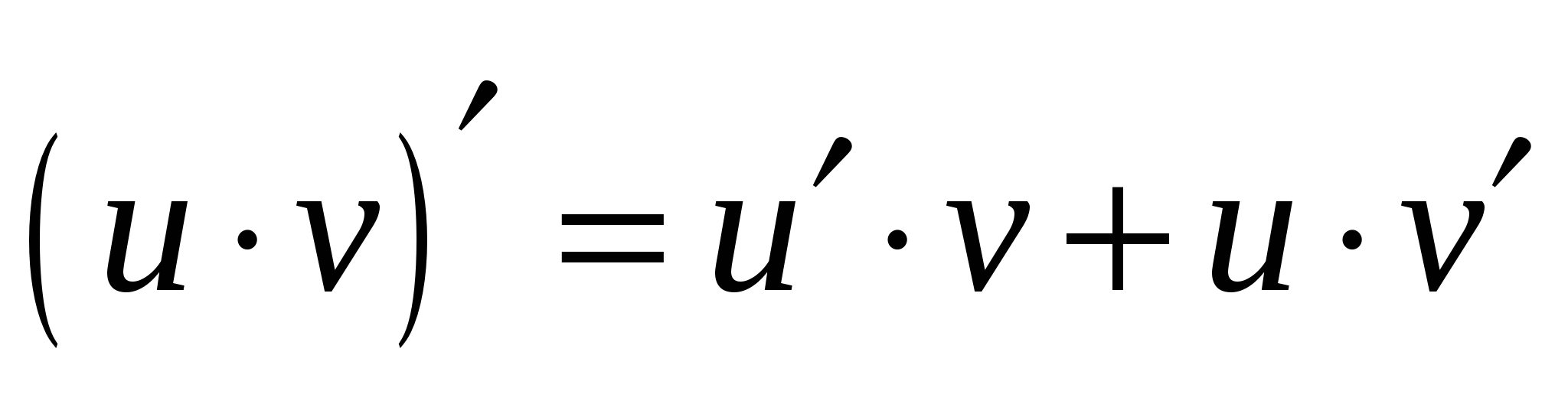
Следствие 1. Постоянный множитель можно выносить за знак производной:
(CU)’=CU’
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:
(UVW)’= U’VW+UV’W+UVW’
-
Производная частного двух дифференцируемых функций может быть найдена по формуле:
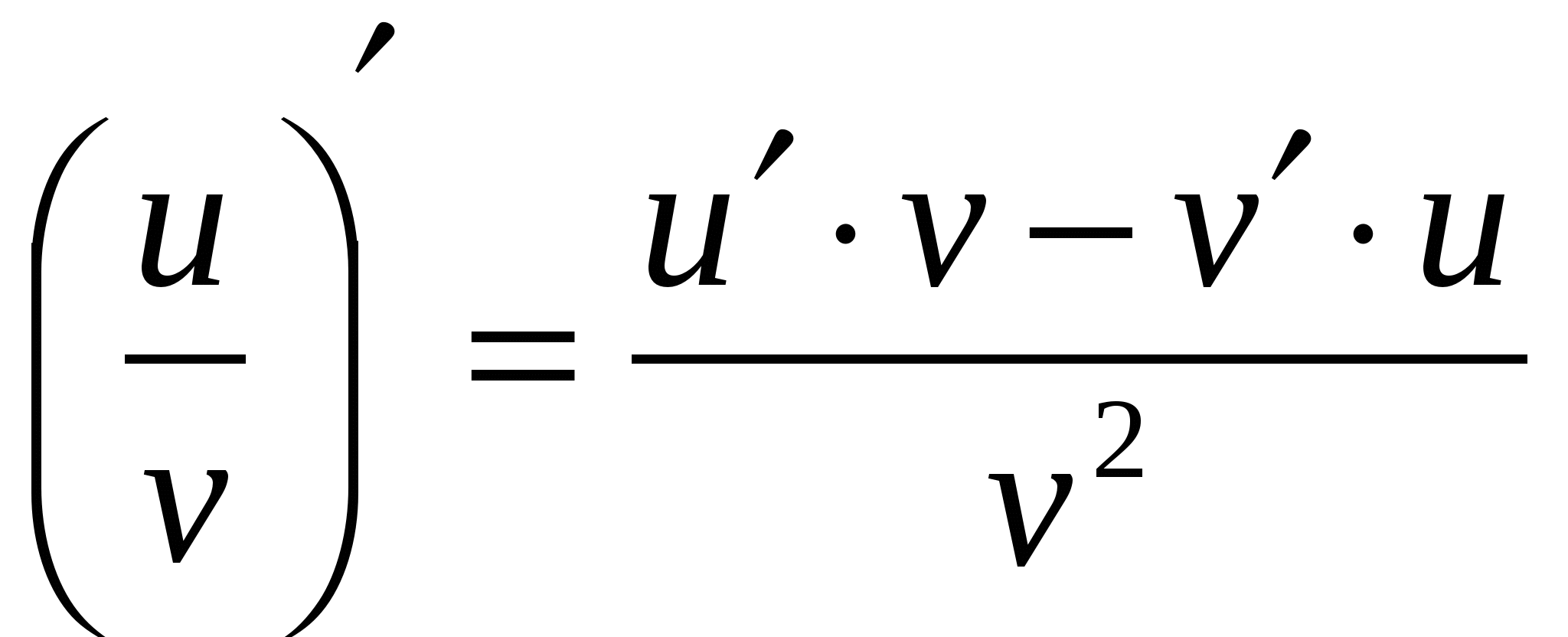
Производная сложной и обратной функции
Пусть переменная
у есть функция от переменной u
(y=f(u)),
а переменная u
в свою очередь есть функция от независемой
переменной х, т.е. задана сложная функция
y=f[![]() (х)] .
(х)] .
Теорема: Если
y=f(u)
и u=![]() (х)
- дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и, умноженной на производную
самого промежуточного аргумента и по
независимой переменной х, т.е.
(х)
- дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и, умноженной на производную
самого промежуточного аргумента и по
независимой переменной х, т.е.
y’=f ‘ (u) * u’
Вся таблица производных из учебника Крамера

Производная обратной функции
Пусть y=f(x) - дифференцируемая и строго монотонная функция на некотором промежутке Х. Если переменную у рассматривать как аргумент, а переменную х - как функцию, то новая функция
у=![]() (у)
является обратной к данной и, как можно
показать, непрерывной на соответствующем
промежутке Y.
(у)
является обратной к данной и, как можно
показать, непрерывной на соответствующем
промежутке Y.
Теорема: для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции:

