лабораторный_практикум_по_жк

зования динамического рассеяния для электрооптического усилителя (рис. 8).

Электрооптический усилитель представляет собой пару: фотопроводник – жидкий кристалл, заключенную между двумя прозрачными электродами. Фотопроводник отделен от жидкого кристалла непрозрачным отражающим слоем. Светочувствительный слой находится под постоянным напряжением, которое подбирается таким образом, что в отсутствии изображения большая часть напряжения падает на фотопроводник. Напряжение на жидком кристалле остается ниже порога перехода в состояние проводимости. Когда же появляется изображение, фотопроводник пропускает ток к жидкому кристаллу, создавая динамическое рассеяние в проводящих точках. На другом конце электрооптического модулятора луч света фокусируется на жидкий кристалл. Когда изображение отсутствует, свет отражается жидким кристаллом и блокируется диафрагмой от попадания на экран. Однако при наличии изображения и, следовательно, при существовании динамического рассеяния в жидком кристалле свет рассеивается за диафрагмой и достигает экрана. Так как свет проекционной лампы во много раз ярче, чем изображение, усиление может быть очень большим (в 1000 раз).

Целью настоящей работы является изучение эффекта ДРС в нематическом кристалле МББА. Измерение интенсивности проходящего света производят с помощью фотодетектора, помещаемого на тубус микроскопа. Ячейка располагается на столике микроскопа в следующих положениях: плоскость поляризации параллельна (направлению натирания стекол); плоскость поляризации перпендикулярна ; в обоих случаях николи параллельны. В двух других случаях анализатор ставится в скрещенное положение относительно поляризатора (образец погашен).

Визуальную картину доменов и ДРС наблюдают в четырех указанных положениях. Затем измеряют зависимость I(V) для этих четырех случаев. Результаты оформляются в виде графика. Необходимо указать, какой визуальной картине соответствуют характерные участки кривых. Зарисуйте в тетради экспериментальную схему измерения ДРС.

41

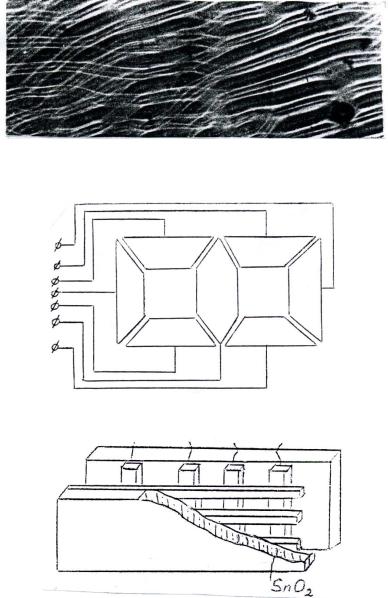
Рис. 5. Визуальная картина возмущенной системы доменов (начальная стадия ДРС)

Рис. 6. Цифровой индикатор

Рис. 7. Матричная система

42

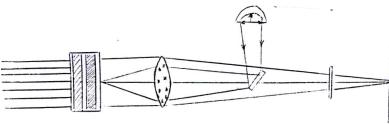
Рис. 8. Электрооптический усилитель

Выполнение работы

1.Установить поляроиды в скрещенное положение.

2.Установить образец МББА с планарной текстурой в положение погасания.

3.Вывести анализатор в параллельное положение.

4.Увеличивая напряжение V, наблюдать эффект ДРС.

5.Аналогичные наблюдения при скрещенных поляроидах и при образце, повернутом на 90о.

6.Записать особенности доменной картины в этих четырех случаях (см. текст работ).

7.Поместить на тубус микроскопа фотонасадку. Измерить зависимость I(V) для четырех возможных случаев положения поляроидов и образца.

8.Нанести полученные кривые на график I(V).

Задания

1.Опишите основные взгляды на механизм ДРС.

2.Объясните характерные особенности полученных кривых, связав их с состоянием образца и поляризацией света.

3.Где применяется эффект ДРС.

43

Лабораторная работа № 5

ОПРЕДЕЛЕНИЕ ДИСПЕРСИИ ДВУЛУЧЕПРЕЛОМЛЕНИЯ НЕМАТИЧЕСКОГО МОНОКРИСТАЛЛА

Двулучепреломление п кристаллических пластин, вырезанных вдоль оптической оси, обычно определяют с помощью компенсаторов, если оно достаточно мало. Величину п можно определить способом канавчатого спектра, если дисперсия двулучепреломления п (λ) (где λ – длина волны) не слишком вели-

пользовать метод канавчатого спектра со специальным способом расчета п.

Нематический монокристалл получают между натертыми в одном направлении стеклами ячейки. Оптическая ось совпадает с направлением директора и направлением натирания.

Теория эксперимента

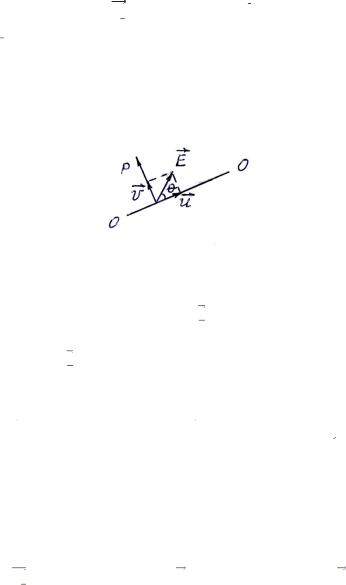
Пусть луч естественного монохроматического света проходит первый поляроид (рис. 1), пропускающий лучи с колебаниями по вертикальной оси ОХ.

Рис. 1. Схема наблюдения кристалла в параллельном поляризованном свете

Уравнение волны после первого поляроида будет:

44

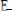
= Ео cos2p(nt – r/ l),

где – единичный вектор по ОХ, а показатель преломления воз-

духа принят п = 1.

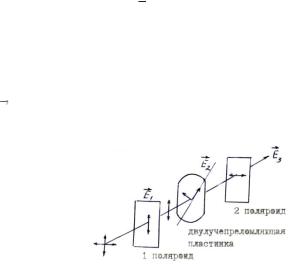
Далее эта волна попадает на двулучепреломляющую пластинку, оптическая ось которой образует см осью ОХ угол q

(рис. 2).

Рис. 2

Тогда внутри пластинки будут распространяться две волны: одна H волна с колебаниями вдоль оптической оси (еди-

ничный вектор, направленный вдоль ОО – U), другая О-волна с колебаниями в перпендикулярном направлении (единичный

вектор, направленный вдоль Р – V). Как следует из рис. 2, уравнение результирующей волны внутри пластинки будет:

= Ео [cosq×cos2p(nt – n or/l) + sinqcos2p(nt – n нr/l].

Ко второму поляроиду придет результирующая волна:

= Ео[cosqcos2p(nt – r/ l) + sinqcos2p(nt – r/ l + d)].

45

Волны с колебаниями по и направлениям после пластинки идут в воздухе, разность фаз между ними не меняется. Амплитуда волны после прохождения пластинки осталась той же Ео, это означает, что мы считаем пластинку (и поляроиды тоже) абсолютно прозрачными. Второй поляроид поставлен так, что пропускает волны с колебаниями Ех только по OY, поэтому им будут пропущены только проекции и волн (рис. 3).

Рис. 3

Через второй поляроид пройдет волна:

= Eo[cosqsinqcos2p(nt – r/ l) – sin qcosqcos2p(nt – r/ l + d)] =

= Eosinqcosq[cos2p(nt – r/ l) – cos2 p(nt – r/ l + d)].

Применим к выражению в квадратных скобках формулу:

cosa – cos b = – 2sin(( a + b)/2)×sin((a – b)/2),

положив a = 2p(nt – r/ l), b = 2p(nt – r/ l + d), тогда

= 2sinqcosqEosin2p(nt – r/ l + d/2)×sin2pd/2 .

Но так как sin 2pd/2 = , то

= Ео · .

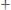
Чтобы получить интенсивность (I) световой волны, прошедшей через поляроиды и пластинку, необходимо найти среднее по времени значение квадрата

46

где I'o – интенсивность падающего на ячейку линейно поляризованного света.

Из (2) следует, что через систему двух поляроидов с двулучепреломляющей пластинкой между ними свет проходит не любых длин волн, а только тех, для которых cos2pd ¹ 1.

Наибольшая интенсивность прошедшего света будет при

не пройдет.

Таким образом, от источника с непрерывным спектром при прохождении света через нашу систему на вход спектросопа получим так называемый «канавчатый» спектр – непрерывный спектр будет пересечен широкими темными полосками, для цветов которых выполняется условие (4). Спектроскоп позволяет измерить длины волн li, соответствующие серединам темных полос. Построив график m(1/li), можно сразу же определить двойное преломление пластинки Dnd как тангенс наклона кривой, а по нему и двойное преломление вещества пластинки Dп.

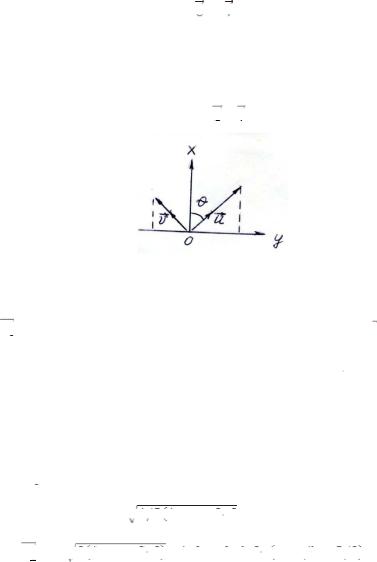
Целью работы является определение длины волны погасания по полосчатому спектру и расчет дисперсии двулучепреломления Dп(l) нематического кристалла МББА (4 – метоксибензилиден – 4 ! – бутиланилина). Спектр наблюдается с помощью спектральной насадки монохроматора (рис. 4).

Зная градуировочную кривую монохроматора l(N), можно получить зависимость m(l), где m – номер линии погасания, начиная с первого в красной области спектра. График зависимости m(l) используется для проверки точности измерений. Его точки должны лежать на гладкой кривой (рис. 5).

47

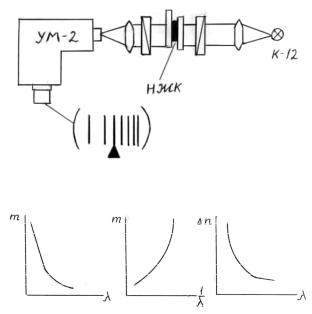
Рис. 4. Схема установки для получения канавчатого спектра

Рис. 5. Экспериментальные графики m( ); m(1/ ) и график ∆n( )

Из (4), полагая для каждой пары точек Dп постоянным, по-

лучим: Dп(li)d×(1/li+1 – 1/ li) = 1.

Тогда Dп(l) можно определить непосредственным расчетом

Dп(li) = d–1 (1/li+1 – 1/ li)–1

и занести результаты в таблицу:

Зависимость Dп(l), полученная таким способом, дает завышенные значения Dп. Это связано с большой дисперсией Dп(l), особенно в области коротких длин волн, где нарушается условие Dп = const для соседних длин волн погасания. Более точные результаты можно получить следующим образом.

48

Предположим, что для участка с минимальной дисперсией (дальний «красный» участок спектра) величина Dп действительно не зависит от l. Тогда можно определить Dп1 для двух соседних «красных» полос погасания по формуле:

(1/l2 – 1/ l1)Dn1×d = 1.

Зная Dп1, определим истинный номер линии погасания.

Р1 = Dп1×d/l1,

отбрасывая десятые и сотые, оставляя целую часть числа. Последующие номера линий погасанияР2 = Р1 + 1, Р3 = Р1 + 2 и т. д. Величины двулучепреломления для соответствующих длин волн определяются как Dп2 = Р2l2/d, Dп3 = Р3 l3/d и т. д.

Таким образом, строится зависимость Dп(l), более близкая к истинной, чем зависимость, определяемая по «тангенсу угла наклона».

В работе требуется определить Dп(l) этими двумя способами.

Выполнение работы

1.Проверить положение поляроидов (скрещенное) на установке с монохроматором УМ-2.

2.Поместить на столик образец с планарной текстурой (d = 30 мкм) МББА. Оптическая ось образца находится под углом 45о по отношению к направлению поляризации.

3.Получить канавчатый спектр поглощения. По шкале ба-

рабана монохроматора определить значения длин волн l для полос погасания, начиная с красной части спектра. Градуировочный график монохроматора прилагается.

4. Построить зависимости, описанные в работе и определить Dп(l) двумя методами расчета: по тангенсу угла наклона; по «истинному» номеру линии погасания.

Вопросы и задания

1.Выведите формулу пропускания и определите условия погасания.

2.Опишите метод канавчатого спектра.

3. Почему второй способ расчета дает более точные значения п(λ)?

49

Лабораторная работа № 6

ДИЭЛЕКТРИЧЕСКАЯ ДЕФОРМАЦИЯ НЕМАТИЧЕСКИХ МОНОКРИСТАЛЛОВ

В жидких кристаллах наблюдается много интересных электрооптических эффектов, не имеющих аналогов в твердых и жидких телах. Даже небольшие внешние электрические поля приводят к значительным искажениям определенной ориентации молекулярных осей (директора) и, следовательно, к изменению оптических свойств мезофазы.

Рассмотрим подробнее ориентационные электрооптические эффекты. Молекулы жидких кристаллов почти всегда имеют постоянный дипольный момент и, если его направление перпендикулярно длинной оси молекул, то диэлектрическая анизотропия вещества в полях низкой частоты отрицательна или

Δε = ε||-ε < 0,

где ε|| – диэлектрическая постоянная образца при параллельной ориентации молекул к направлению электрического поля, а ε – диэлектричская постоянная при перпендикулярной ориентации. Вещества, молекулы которых обладают постоянным дипольным моментом в направлении, параллельном длинной оси, в полях низкой частоты имеют положительную анизотропию или

Δε = ε|| – ε > 0.

Согласно законам электростатики, в постоянных полях и полях низкой частоты молекулы должны устанавливаться таким образом, чтобы их постоянные дипольные моменты были параллельны вектору напряженности Е, поэтому в веществах с Δε > 0 молекулы должны ориентироваться параллельно полю, в то время как для веществ с Δε < 0 – перпендикулярно полю.

Важное место в электроптических эффектах занимает индуцированное электрическим полем двулучепреломление образца. Двулучепреломление изменяется вследствие деформации ориентации нематического образца. Эффект называется переходом Фредерикса (по имени ученого, открывшего его).

50