
- •1 Множества и операции над ними! Введение
- •Множества и операции над ними
- •1.1. Множества и способы их задания
- •Определение
- •[Править]Пример
- •[Править]Свойства
- •[Править]Связанные определения
- •Используемые определения
- •[Править]Определения
- •[Править]Замечание
- •[Править]Примеры
- •[Править]Теорема о гранях
- •[Править]Доказательство
- •[Править]Свойства
- •Формулировка
- •[Править]Замечание
- •[Править]Доказательство
- •[Править]Лемма о вложенных отрезках и полнота (непрерывность) поля вещественных чисел
- •Определение
- •[Править]Примеры
- •Определение
- •Сходящиеся и расходящиеся последовательности
- •[Править]Свойства сходящихся последовательностей
Определение
Два множества называются равномощными, если между ними существует биекция. Существование биекции между множествами есть отношение эквивалентности, а мощностьмножества — это соответствующий ему класс эквивалентности. Класс множеств, биективно эквивалентных данному, не является, однако, множеством (подробнее о классах см. в книге: Келли. Общая топология. (Приложение в конце книги)).
[Править]Пример
Множество
чётных целых чисел ![]() имеет
такую же мощность, что и множество целых
чисел
имеет
такую же мощность, что и множество целых
чисел ![]() .
Определим
.
Определим ![]() так:
так: ![]() .
.
![]() —
биекция, поэтому
—
биекция, поэтому ![]()
[Править]Свойства
Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества.
Для бесконечных множеств мощность множества может совпадать с мощностью своего собственного подмножества, например
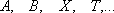 .
.Более того, множество бесконечно тогда и только тогда, когда оно содержит равномощное собственное (то есть не совпадающее с основным множеством) подмножество.
Теорема Кантора гарантирует существование более мощного множества для любого данного: Множество всех подмножеств множества A имеет большую мощность, чем A, или
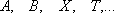 .
.С помощью канторова квадрата можно также доказать следующее полезное утверждение: Декартово произведение бесконечного множества A с самим собой равномощно A.
Мощность декартова произведения:
![]()
Формула включения-исключения в простейшем виде:
![]()
[Править]Связанные определения
Мощность
множества натуральных чисел ![]() обозначается
символом
обозначается
символом ![]() («алеф-нуль»).
Множество называется бесконечным,
если его мощность
(«алеф-нуль»).
Множество называется бесконечным,
если его мощность ![]() (не
меньше мощности множества натуральных
чисел), таким образом, счётные
множества —
это «самые маленькие» из бесконечных
множеств. Следующие кардинальные числа
в порядке возрастания обозначаются
(не
меньше мощности множества натуральных
чисел), таким образом, счётные
множества —
это «самые маленькие» из бесконечных
множеств. Следующие кардинальные числа
в порядке возрастания обозначаются ![]() (где
индекс пробегает все порядковые
числа).
Среди кардинальных чисел нет наибольшего:
для любого множества кардинальных чисел
существует кардинальное число, большее
всех элементов этого множества.
(где
индекс пробегает все порядковые
числа).
Среди кардинальных чисел нет наибольшего:
для любого множества кардинальных чисел
существует кардинальное число, большее
всех элементов этого множества.
Про
множества, равномощные множеству
всех вещественных
чисел,
говорят, что они имеют мощность
континуума,
и мощность таких множеств обозначается
символом ![]() .
Предположение о том, что
.
Предположение о том, что ![]() ,
называется континуум-гипотезой.
,
называется континуум-гипотезой.
Для
мощностей, как и в случае конечных
множеств, имеются понятия: «равенство»,
«больше», «меньше». То есть для любых
множеств ![]() и
и ![]() возможно
только одно из трёх:
возможно
только одно из трёх:
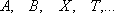 ,
или
,
или 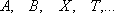 и
и 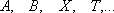 равномощны;
равномощны;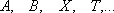 ,
или
,
или 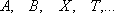 мощнее
мощнее 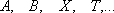 ,
т. е.
,
т. е. 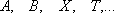 содержит
подмножество, равномощное
содержит
подмножество, равномощное 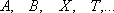 ,
но
,
но 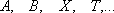 и
и 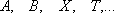 не
равномощны;
не
равномощны;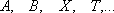 ,
или
,
или 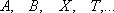 мощнее
мощнее 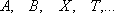 —
в этом случае
—
в этом случае 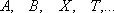 содержит
подмножество, равномощное
содержит
подмножество, равномощное 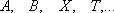 ,
но
,
но 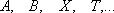 и
и 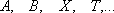 не
равномощны.
не
равномощны.
Ситуация,
в которой ![]() и
и ![]() не
равномощны и ни в одном из них нет части,
равномощной другому, невозможна. Это
следует из теоремы Цермело. Иначе это
означало бы существование несравнимых
между собой мощностей (что в принципе
возможно, если не принимать аксиому
выбора).
не
равномощны и ни в одном из них нет части,
равномощной другому, невозможна. Это
следует из теоремы Цермело. Иначе это
означало бы существование несравнимых
между собой мощностей (что в принципе
возможно, если не принимать аксиому
выбора).
Ситуация,
в которой ![]() и
и ![]() ,
невозможна по теореме
Кантора — Бернштейна.
,
невозможна по теореме
Кантора — Бернштейна.
3.ГРАНИЦЫ И ТОЧНЫЕ ГРАНИЦЫ МНОЖЕСТВ.
Используемые определения
Мажоранта или верхняя
грань (граница) множества ![]() —
число
—
число ![]() ,
такое что
,
такое что ![]() .
Миноранта или нижняя
грань (граница) множества
.
Миноранта или нижняя
грань (граница) множества ![]() —
число
—
число ![]() ,
такое что
,
такое что ![]()
