Применение степенных рядов к приближенным вычислениям

Рассмотрим применение вещественных степенных рядов к приближенным вычислениям.

Во-первых, ряд Тейлора, и в частности ряд Маклорена в случае его сходимости, дает возможность приближенно вычислять значения функции , заменяя их конечным числом членов разложения по формуле (5.29).

Чем меньше , тем меньше членов можно брать в этом разложении для вычисления с желаемой точностью. Если весьма мало, то иногда достаточно ограничиться только первыми двумя членами, отбросив все остальные. Таким образом, получается очень простая приближенная формула для , которая при малых вполне может заменить часто довольно сложное точное выражение для . Например, из разложения функции в ряд Маклорена следует, что

Аналогично могут быть получены формулы:

Пользуясь этими приближенными формулами при , близких к нулю (положительных или отрицательных), можно значительно упростить сложные выражения.

Во-вторых, с помощью рядов можно вычислять определенные интегралы.

Большое значение, например, в теории вероятностей имеет интеграл

который не может быть выражен в элементарных функциях. Для его вычисления заменим в формуле (5.31) на. Тогда

.

Радиус сходимости полученного ряда равен , т.е. на любом замкнутом промежуткеэтот ряд сходится равномерно. Это позволяет почленно проинтегрировать его, что дает следующее равенство:

В-третьих, при помощи степенных рядов можно также приближенно интегрировать разнообразные дифференциальные уравнения. Не вдаваясь в сложные теоретические соображения, ограничимся рассмотрением примеров.

Пример 5.22. Решить задачу Коши для уравнения первого порядка

Решение. Полагая из уравнения и начального условия находим

Если продифференцировать обе части уравнения, а затем положить и использовать полученное равенства и начальные условия, то получим

Аналогично приходим к равенствам

и т. д. Подставляя полученные значения в формулу Маклорена, имеем

.

Этой формулой можно пользоваться при небольших значениях .

Для решения дифференциальных уравнений широко используются также степенные ряды с неопределенными коэффициентами. Рассмотрим пример.

Пример 5.23. Решить уравнение второго порядка

Решение. Будем искать решение в виде ряда по степеням

.

После дифференцирования этого ряда и подстановки его в уравнение, получим следующее равенство

Приравнивание нулю коэффициентов при дает систему уравнений

откуда последовательно находим коэффициенты ряда

и т.д.

Подстановка этих результатов в степенной ряд дает общее решение рассматриваемого уравнения:

Константы и остаются в качестве произвольных постоянных. Ряды же, стоящие в скобках, представляют собой два линейно независимых частных решения исходного уравнения.

Решение задач

Задача 5.8. Исследовать область сходимости функционального ряда

.

Решение. Так как при всех x и n , а ряд, будучи геометрическим, со знаменателем геометрической прогрессии, сходится, то, согласно признаку Вейерштрасса, данный ряд сходится равномерно для всех вещественныхx.

Задача 5.9. Исследовать область сходимости степенного ряда

.

Решение. В данном случае ,. Найдем радиус сходимости ряда, используя признак Даламбера. Для этого вычислим предел отношения последующего члена ряда к предыдущему:

Полученный предел, в соответствии с признаком Даламбера, для сходящегося ряда должен быть меньше единицы, т.е. . Отсюда мы получаем неравенство, определяющее интервал сходимости ряда. Искомый радиус сходимости будет . Следовательно, рассматриваемый ряд абсолютно сходится для значений , удовлетворяющих неравенству или .

Исследуем сходимость ряда на концах промежутка. Если , то мы получаем знакочередующийся числовой ряд

,

который является рядом Лейбница и сходится. Причем сходится неабсолютно, так как ряд, составленный из абсолютных величин членов исходного ряда, расходится, будучи гармоническим рядом.

Если же , то получается гармонический ряд

,

который расходится. Итак, исходный ряд сходится абсолютно при и сходится условно при .

Замечание. При вычислении радиуса сходимости с помощью формулы , где и - коэффициенты степенного ряда

,

будет получен тот же результат. Но следует быть внимательным в случае, когда в ряде пропущено бесконечно много членов, например, четной или нечетной степени. В этом случае лучше непосредственно применять признак Даламбера. Рассмотрим пример.

Задача 5.10. Найти область сходимости и радиус сходимости степенного ряда

.

Решение. Этот ряд содержит члены только с нечетной степенью, а бесконечное число членов с четной степенью отсутствует. Для нахождения области сходимости и радиуса сходимости применим непосредственно признак Даламбера.

Здесь общий член ряда и следующий за ним член соответственно равны

, .

Вычислим предел их отношения

Полагая найденный предел меньше единицы, т.е. , приходим к неравенствуили.

Искомый радиус сходимости , интервал сходимости или . Подстановка в заданный ряд илиприводит соответственно к рядам

и ,

которые получаются из расходящегося гармонического ряда почленным умножением на и на. Эти ряды также расходятся в соответствии со свойством умножения ряда на число. Таким образом, областью сходимости заданного ряда будет интервал2<x<8.

Задача 5.11. Написать разложение в ряд Тейлора функции

в окрестности точки , т.е. написать разложение функции по степеням.

Решение. Разложим данную дробно-рациональную функцию на сумму простейших дробей.

.

Коэффициенты инаходятся из тождества, которое верно для любого значения. Полагая , получим , затем, полагая, будем иметь. Следовательно, .

Представим каждое из слагаемых, стоящих в правой части этого равенства, в виде геометрического ряда, расположенного по степеням . Для этого первое слагаемое представим в виде

.

Дробь, стоящую справа, можно рассматривать как сумму геометрической прогрессии с первым членом 1 и знаменателем

В итоге для первого слагаемого имеем:

.

Это разложение имеет место для т.е. дляили.

Вторую простейшую дробь, стоящую в правой части равенства, запишем в виде

.

Выражение представляет собой сумму геометрической прогрессии, первый член которой, а знаменатель. Следовательно, для второго слагаемого можно записать

или в сокращенной записи

.

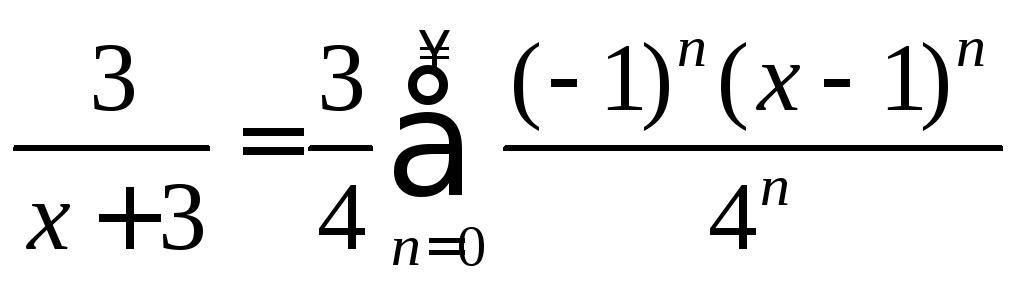Этот ряд сходится при условии , т.е. дляили.

Подставляя найденные разложения в правую часть равенства , получим

.

Окончательно, искомое разложение имеет следующий вид

.

Построенное разложение имеет место в области перекрытия областей сходимости и, т.е. для.

Задача 5.12. Разложить в ряд Маклорена функцию .

Решение. В этом примере ищется разложение функции в ряд по степеням x. Воспользуемся известным разложением

.

Для этого преобразуем заданную функцию к виду , и в разложениивместоx подставим 2x:

.

Итак, искомое разложение функции имеет следующий вид

.

Так как разложение для имеет место на всей числовой оси, то и построенное разложение функции справедливо для любого.

Задача 5.13. Решить задачу Коши для уравнения второго порядка

при начальных условиях .

Решение. Искомое решение запишем в виде

или , т.к..

Значение находим из заданного уравнения при .

Чтобы найти ,последовательно дифференцируем исходное уравнение

,

,

,

,

……………….……………………………………

,,

…………………………………………………………….

Подставляя эти значения производных в разложение для , получим искомое решение задачи Коши

или