Например, таким рядом будет

Если последовательность чисел имеет вид то соответствующий ей ряд запишется в виде

Сам по себе символ (5.1) никакого определенного смысла не имеет, потому что действие сложения в своем непосредственном содержании имеет дело каждый раз лишь с конечным числом слагаемых, т.е. смысл выражению (5.1) предстоит приписать нам самим. Формулировки различных определений числового ряда и сопоставление их друг с другом представляют большой интерес как теоретический, так и практический. Однако мы сейчас ограничимся рассмотрением лишь одной такой формулировки.

Определение 5.1. Сумма первыхчленов ряда (5.1) называется -й частичной суммой этого ряда.

Ряд (5.1) называется сходящимся, если последовательность его частичных сумм имеет конечный предел

Значение этого предела называетсясуммой ряда (5.1). В этом случае пишут Тем самым символупридается определенныйчисловой смысл.

Определение 5.2. Ряд (5.1) называется расходящимся, если последовательность его частичных сумм не имеет конечного предела.

Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов. Простейшим примером числового ряда является геометрический ряд

(5.2)

члены которого образуют известную нам геометрическую прогрессию. Исследуем геометрический ряд на сходимость.

С этой целью рассмотрим частичную сумму

(5.3)

и изучим ее поведение при Очевидно, что поведениебудет зависеть от значения

Пусть тогда, умножая обе части равенства (5.3) наи вычитая полученное равенство из (5.3), мы будем иметьОткуда следует

(5.4)

Очевидно, что поведение приопределяется поведением второго слагаемого, содержащего

Известно, что если топрии, значит, частичная сумма рядабудет стремиться кприПоэтому геометрический ряд присходится, и его сумматак что мы можем написать

При величинав равенстве (5.4) не имеет конечного предела прии, следовательно, пригеометрический ряд расходится.

Если то частичная сумма равнаи, значит, геометрический ряд прирасходится, так как

Остается рассмотреть В этом случае мы получаем ряд

Частичная сумма равна нулю, если- четное, и равна, если- нечетное, таким образом,не имеет предела, и поэтому приряд расходится.

Итак, геометрический ряд (5.2) сходится только при

Пример 5.1. Исследовать на сходимость ряд

Решение. Найдем его частичную сумму Имеем

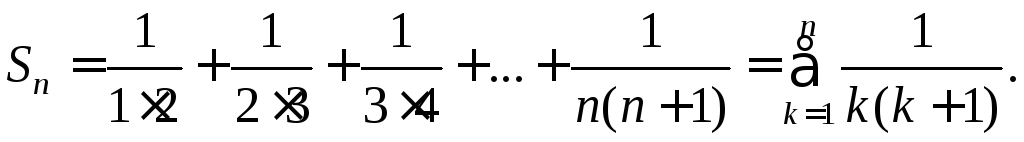
Эту частичную сумму можно упростить, если заметить, что

Итак, для частичной суммы получим

Очевидно, что приСледовательно, заданный ряд сходится, и его суммаравна 1, так что мы можем написать

Пример 5.2. Исследовать на сходимость ряд

Решение. Найдем частичную сумму этого ряда. Имеем

или

Так как

то заданный ряд расходится. При этом мы можем написать

.

Сходящиеся числовые ряды обладают некоторыми свойствами, которые позволяют действовать с ними, как с конечными суммами.

Свойства сходящихся числовых рядов

1) Если ряд (5.1) сходится и имеет сумму , то ряд

также сходится и его сумма равна .

2) Сходящиеся ряды можно почленно складывать и вычитать, т.е. если

то ряды итакже сходятся, и их суммы равны соответственнои. Это утверждение можно записать в виде такого равенства

3) Свойство сходимости или расходимости ряда не нарушается, если у ряда отбросить или приписать к нему любое конечное число членов с начала.

4) (Необходимый признак сходимости ряда). Общий член сходящегося ряда стремится к нулю при

Пример 5.3. Покажем, что ряд

расходится.

Решение. Действительно, для этого ряда

т.е. необходимый признак сходимости ряда не выполняется, следовательно, ряд расходится.

Подчеркнем, что необходимый признак сходимости является необходимым, но не достаточным. В дальнейшем мы познакомимся с многочисленными рядами, для которых но которые, тем не менее, расходятся. Здесь же приведем в качестве примера ряд

который называется гармоническим^ рядом, и который расходится, в чем мы убедимся чуть позднее, хотя общий член этого ряда стремится к нулю при .

Числовые неотрицательные ряды. Признаки сравнения

Рассмотрим ряд все члены которого неотрицательны, так чтоТакой ряд носит названиенеотрицательного.

Во многих задачах, теоретических и практических, необходимо установить лишь сам факт сходимости или расходимости числового ряда. Например, сходимость ряда можно установить, составив последовательность его частичных сумм и выяснив, имеет ли эта последовательность конечный предел. Этот признак является, очевидно, необходимым и достаточным признаком сходимости рядов. Стремление к нулю общего члена ряда по мере роста его номера также является признаком сходимости ряда, однако только необходимым, но не достаточным.

В дальнейшем будем рассматривать ряды, у которых общий член положителен, т.е. Такие ряды называют положительными.

Необходимый и достаточный признак сходимости положительного ряда дает следующая теорема.

Теорема 5.1. Для того чтобы положительный ряд сходился, необходимо и достаточно, чтобы его частичные суммыбыли ограничены сверху

Приведенная теорема является основной теоремой теории положительных рядов. Этой теоремой можно воспользоваться при доказательстве расходимости гармонического ряда. Именно неограниченность частичных сумм гармонического ряда и является причиной его расходимости.

Указанная теорема о необходимом и достаточном условии сходимости положительного ряда на практике применяется редко, так как она требует нахождения оценки частичной суммы ряда, что удается сделать лишь в редких случаях. Желательно иметь в своем распоряжении признаки сходимости, основанные на оценках только общего члена ряда. При этом естественно возникает вопрос, нельзя ли, зная поведение одного ряда, судить о поведении другого ряда путем сравнения их общих членов. Оказывается, можно. Соответствующие признаки сходимости (расходимости) называются признаками сравнения.

Теорема 5.2. (Первый признак сравнения). Пусть даны два положительных ряда

(5.5)

и

(5.6)

причем члены первого ряда, начиная с некоторого номера не превосходят соответствующих членов второго ряда:

Тогда из сходимости ряда (5.6) следует сходимость ряда (5.5), а из расходимости ряда (5.5) следует расходимость ряда (5.6).

Пример 5.4. Исследовать сходимость ряда

(5.7)

Решение. Сравним данный ряд с рядом:

, (5.8)

который сходится (см. пример 5.1). Имеем:

т.е.

(5.9)

Так как ряд (5.8) сходится, то, учитывая неравенство (5.9), согласно первому признаку сравнения, сходится и ряд (5.7).

Во многих случаях в качестве рядов сравнения берут геометрический или гармонический ряды.

Пример 5.5. Исследовать на сходимость ряд

Решение. Сравним этот ряд с гармоническим рядом . ИмеемНо гармонический ряд расходится. Следовательно, по первому признаку сравнения, заданный ряд тоже расходится.

Теорема 5.3. (Второй признак сравнения). Пусть даны два положительных ряда (5.5) и (5.6), причем можно указать такие постоянные ичто, начиная с некоторого, выполняются неравенства

Тогда ряды (5.5) и (5.6) одновременно сходятся или одновременно расходятся.

Следствие. Если для рядов (5.5) и (5.6) отношение стремится к некоторому конечному положительному пределу

то указанные ряды сходятся или расходятся одновременно. Это следствие более удобно для практического применения чем непосредственное использование второго признака сравнения.

Пример 5.6. Исследовать сходимость ряда

Решение. Сравним исходный ряд с рядом , общий член которого равени является членом геометрической прогрессии со знаменателемЧтобы воспользоваться вторым признаком сравнения, вычислим предел: Так как найденный предел конечен и отличен от нуля, а ряд сравнения сходится, то, согласно второму признаку сравнения, сходится и данный ряд.

Пример 5.7. Исследовать сходимость ряда

Решение. Сравним исходный ряд с гармоническим рядом общий член которого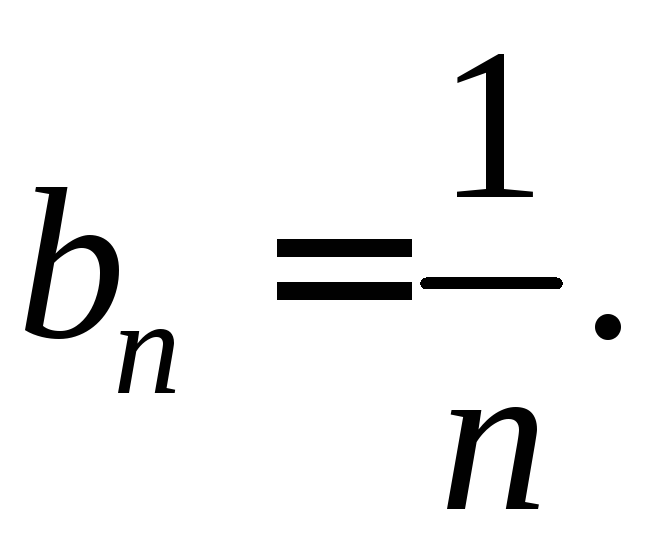

Так как предел конечен и отличен от нуля, и гармонический ряд расходится, то, согласно второму признаку сравнения, данный ряд расходится.