Решение задач

Задача 1.1. Решить уравнение при.

Данное дифференциальное уравнение есть уравнение с разделяющимися переменными. Функции инепрерывны при любых значенияхи.

Считая пока, что и умножив обе части данного уравнения на дробь, получим:

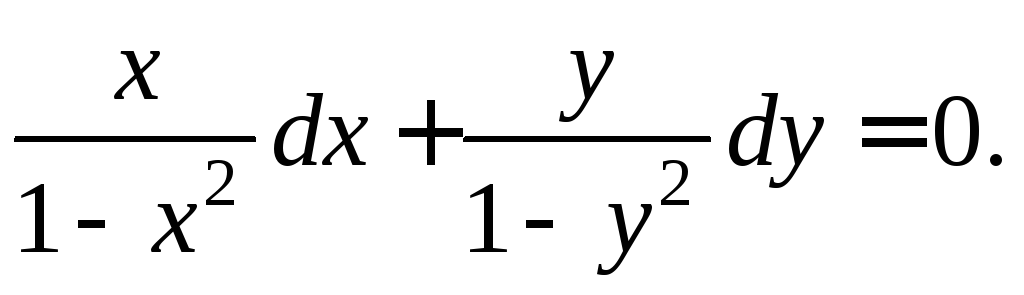(1.46)

Умножая уравнение (1.46) на число и замечая, что при этом в числителе каждой дроби стоит производная знаменателя, сможем написать в результате интегрированиягде произвольная постоянная обозначена через, что возможно, если принять. Последнее равенство можно записать в виде Мы получили общий интеграл данного уравнения при условии

Рассмотрим теперь случай , т.е.Непосредственно из данного уравнения видно, что каждый из случаевиявляется решением. При этом они содержатся в общем интеграле и могут быть получены из него при.

Задача 1.2. Решить уравнение при.

Для установления типа данного уравнения умножим обе его части на . Получим уравнение, которое является уравнением с разделяющимися переменными.

Для решения последнего уравнения умножим обе части на . Будем иметьили в таком виде:.

Выполняя операции интегрирования, сможем написать где- произвольная постоянная. Разрешая относительно, получим окончательногде произведениевновь обозначено через.

Задача 1.3. Для найти решение уравнения

, (1.47)

удовлетворяющее начальному условию .

Вначале заметим, что правая часть данного уравнения является однородной функцией нулевой степени и, кроме того, она непрерывна и не обращается в нуль в любой области , не содержащей начала координат системы.

Введем подстановку , где- новая неизвестная функция. Уравнение (1.47) при этом имеет вид

.

Сократив в правой части уравнения на отличный от нуля множитель , получим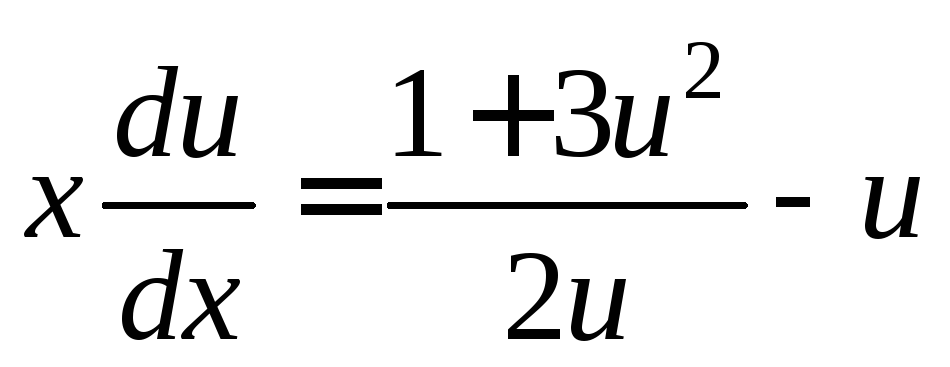. Упростив и разделив переменные, сможем написать. Выполняя интегрирование, будем иметьгде- произвольное положительное число. Из последнего равенства следует, что

Возвращаясь к искомой функции , получим общий интеграл уравнения (1.47) в виде

(1.48)

Для отыскания частного интеграла, удовлетворяющего заданному начальному условию, положим в (1.48) . Получим. Если подставитьв равенство (1.48), то сможем записать искомый частный интеграл в виде

Задача 1.4. Найти решение уравнения удовлетворяющее начальному условию.

Приведем данное уравнение к виду (1.25), для чего разделим обе его части на . Получим

(1.49)

В нашем случае имеем

Для того чтобы найти общее решение уравнения (1.49), воспользуемся формулой (1.30), для чего выпишем вначале величины, входящие в нее

Подставив эти выражения в формулу (1.30), получим

. (1.50)

Для нахождения искомого частного решения положим в (1.50) , а,, откуда следует.

Искомое частное решение имеет вид

Задача 1.5. Решить уравнение при

. (1.51)

Если считать за аргумент, аза функцию, то это уравнение не является линейным. Если же за независимую переменную принять, аза искомую функцию, то данное уравнение можно привести к виду (1.25).

Запишем данное уравнение сначала в виде а затем в виде

Разделив обе части последнего уравнения на , получим линейное уравнение относительно неизвестной функции

(1.52)

В согласии с формулой (1.30), в которой следует ипоменять местами, получим выражение для общего решения уравнения (1.51)

Вычисляя интегралы, сможем написать илиоткуда следует

Вычисляя интеграл, получим окончательно общий интеграл данного дифференциального уравнения

Задача 1.6. Проинтегрировать уравнение при начальном условиии вычислить значение функциипри.

Данное уравнение - линейное дифференциальное уравнение первого порядка. Запишем его в виде , разделив обе части уравнения на(при).

.

Здесь .

Воспользуемся формулой общего решения линейного уравнения

.

Так как , то

.

Для имеем

.

; .

Получили общее решение уравнения: .

Решим задачу Коши: найдем частное решение, удовлетворяющее начальным условиям , т.е. то значение произвольной постоянной, при котором. Поставимив общее решение. Получим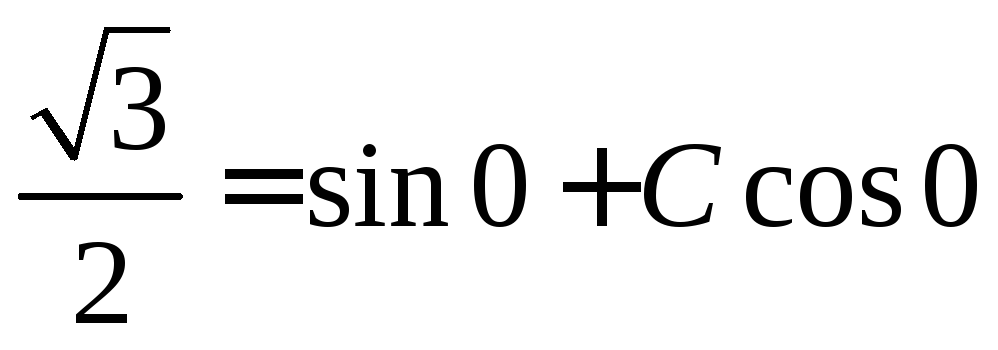, отсюда. Тогда- частное решение, удовлетворяющее начальным условиям. Вычислим значение функциив точке.

.

Ответ:

Замечание. При решении задачи вводили ограничение , но полученное- общее решение является таковым и при, ане является вообще решением.