Сделаем подстановку (1.18)

где - новая неизвестная функция и вычислим

. (1.19)

Подставив (1.18) и (1.19) в уравнение (1.17), получим , но так как- однородная функция нулевой степени, то сможем написатьили считая, что, а это уравнение с разделяющимися переменными, в котором- неизвестная функция.

Пример 1.3. Решить уравнение при :

(1.20)

Функция определена в областитак какимеет смысл лишь при. Данное уравнение является однородным, так как функция- однородная функция нулевой степени относительно своих аргументов в указанной области, ибо

Введем подстановку , где- новая неизвестная функция. При этом. Осуществив подстановку, получимоткуда следует уравнение с разделяющимися переменными

(1.21)

Решая его в области , будем иметь

или, выполняя интегрирование

где произвольная постоянная записана в виде при условииИз последнего равенства следует

(1.22)

Очевидно, что если , то, если же, то, а тогда, считая, что произвольная постояннаяможет принимать и отрицательные значения, сможем записать равенство (1.22) в видеили

. (1.23)

При разделении переменных считалось, что . Непосредственно видно, чтоявляется решением уравнения (1.21) и что оно не потеряно, а содержится в семействе (1.23) при. Возвращаясь к старой переменной, получим- общее решение уравнения (1.20) в области, где- любое число.

Заметим, что если и- однородные функции одной и той же степени, которые непрерывны в некоторой областии не обращаются одновременно в нуль ни в одной точке этой области, то дифференциальное уравнение

(1.24)

также является однородным и с помощью подстановки (1.18) приводится к уравнению с разделяющимися переменными.

Линейные уравнения первого порядка

Рассмотрим третий тип дифференциальных уравнений первого порядка интегрируемых в квадратурах.

Определение. Дифференциальное уравнение первого порядка называется линейным, если оно может быть записано в виде

(1.25)

где -искомая функция аргумента, аи- заданные непрерывные функции на промежутке. Отметим специально, что данное уравнение линейно относительно искомой функциии ее производной.

Легко видеть, что в согласии с теоремой 1.1 уравнение (1.25) имеет единственное решение , удовлетворяющее условию где начальное значениеможно выбирать произвольным, а значение брать любым из промежутка .

Если всюду в, то уравнение (1.25) называютлинейным однородным уравнением или линейным уравнением без правой части. В противном случае его называют линейным неоднородным уравнением или линейным уравнением с правой частью.

В частности, однородное линейное уравнение имеет решение , называемоенулевым или тривиальным.

Существует несколько методов решения линейных дифференциальных уравнений. Остановимся на двух из них.

Метод вариации произвольной постоянной (метод Лагранжа). Рассмотрим вначале однородное уравнение

(1.26)

Заметим, что так как уравнение (1.26) имеет нулевое решение в, то ни одно решение этого уравнения не может обратиться в нуль ни в одной точке промежутка, ибо в этой точке нарушилась бы теорема 1.1. Это означает, что любое решение уравнения (1.26) не меняет знака, т.е. график решения лежит либо выше оси, либо ниже оси.

Рассмотрим случай, когда . Легко видеть, что уравнение (1.26) является уравнением с разделяющимися переменными. Разделяя переменные, можем написатьили. Интегрируя, получимгде- произвольная положительная постоянная. После потенцирования найдем

(1.27)

Для случая получим аналогичное выражение, у которого. Если заметить, что привыражение (1.27) дает решение, то можно утверждать, что равенство (1.27) представляет собою общее решение однородного уравнения (1.26) в полосе, если считатьпроизвольной постоянной.

Перейдем теперь к решению неоднородного уравнения (1.25). В согласии с методом Лагранжа будем искать его решение в виде формулы (1.27), заменяя в ней произвольную постоянную некоторой, пока неизвестной и непрерывно дифференцируемой нафункцией, т.е.

(1.28)

где функцию нужно выбрать так, чтобы функция (1.28) была решением уравнения (1.25) (варьируем произвольную постоянную). Подставляя (1.28) в уравнение (1.25), имеем

откуда или

Выполняя интегрирование, будем иметь

(1.29)

где - произвольная постоянная. Подставив (1.29) в (1.28), получим выражение

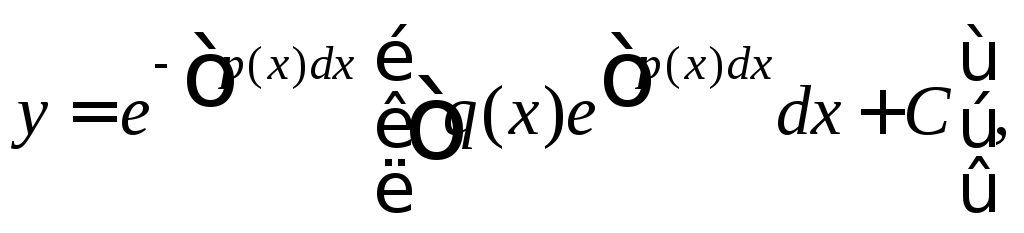(1.30)

которое представляет собою общее решение уравнения (1.25) в полосе

Метод И.Бернулли. В согласии с этим методом будем искать решение уравнения (1.25) в виде произведения двух непрерывно дифференцируемых на промежутке функцийи, одна из которых может быть выбрана по нашему желанию, а другая определяется с помощью уравнения (1.25), так что

(1.31)

Подставив (1.31) в уравнение (1.25), получим (опуская аргумент

или в таком виде:

(1.32)

Реализуем теперь свое право выбора функции , взяв в качестве ее такую, чтобы коэффициент при(т.е. выражение, стоящее в круглых скобках) равнялся нулю

(1.33)

Для этого в качестве надо взять любое ненулевое решение уравнения (1.33). Уравнение вида (1.33) было решено выше и его общее решение имеет вид (1.27). Для получения искомого решения проще всего взять, и тогда получим

(1.34)

Подставив (1.34) в уравнение (1.32), имеем уравнение для определения функции :

, откуда

Выполняя интегрирование, сможем записать

(1.35)

где - произвольная постоянная. Подставив (1.34) и (1.35) в (1.31), получим общее решение уравнения (1.25) в виде (1.30).

Пример 1.4. Решить уравнение

(1.36) для двумя методами: Лагранжа и Бернулли.

1. В согласии с методом Лагранжа рассмотрим сначала однородное уравнение

(1.37)

Разделяя переменные, можем написать или. Выполняя интегрирование, получим общее решение уравнения (1.37)

(1.38)

где - произвольная постоянная. По методу Лагранжа будем искать решение неоднородного уравнения (1.36) в виде (1.38), но вместо произвольной постояннойвозьмем некоторую непрерывно дифференцируемую функцию, так что решение получим в виде

(1.39)

Подставив (1.39) в уравнение (1.36), сможем написать , откуда следует

Интегрируя, найдем

(1.40)

где - произвольная постоянная. Подставив (1.40) в (1.39), получим общее решение уравнения (1.36) на плоскостив виде

2. Следуя методу И.Бернулли, будем искать решение уравнения (1.36) в виде

(1.41)

где и- непрерывно дифференцируемые функции, одна из которых может быть выбрана произвольно. Подставив (1.41) в (1.36), получим

или (1.42)

Выберем функцию так, чтобы коэффициент приравнялся тождественно нулю, т.е.

(1.43)

Решая уравнение (1.43) точно так же, как и уравнение (1.37), найдем его общее решение в виде где- произвольная постоянная, а положив, найдем частное решение

(1.44)

Подставив (1.44) в уравнение (1.42), сможем написать или, откуда в результате интегрирования получим

(1.45)

где - произвольная постоянная. Подставляя (1.44) и (1.45) в (1.41), получим то же самое решение, что и по методу Лагранжа.