Решение задач

Задача 3.1. Проверить, является ли совокупность двух функций

(3.22)

общим решением системы (3.23)

в интервале и, если является, найти частное решение, удовлетворяющее начальным условиям.

Функции (3.22) разрешимы относительно и и при любых и должны при подстановке их в систему (3.23) обратить каждое уравнение системы в тождество для любого. Найдем производные, подставим их в систему (3.23). В левых частях уравнений получим выраженияи, в правых частях уравнений получими. В итоге имееми. Итак, система функций (3.22) – общее решение системы (3.23).

Найдем частное решение, удовлетворяющее начальным условиям, для этого подставим в (3.22) для определения и

, откуда и- частное решение системы (3.23), удовлетворяющее начальным условиям.

Задача 3.2. Найти решение системы , (3.24)

удовлетворяющее начальным условиям

. (3.25)

Дана линейная система двух обыкновенных дифференциальных уравнений с постоянными коэффициентами. Используем метод Эйлера для ее решения. Ищем решение системы (3.24) в виде

. (3.26)

Подставим (3.26) в систему (3.24), получим

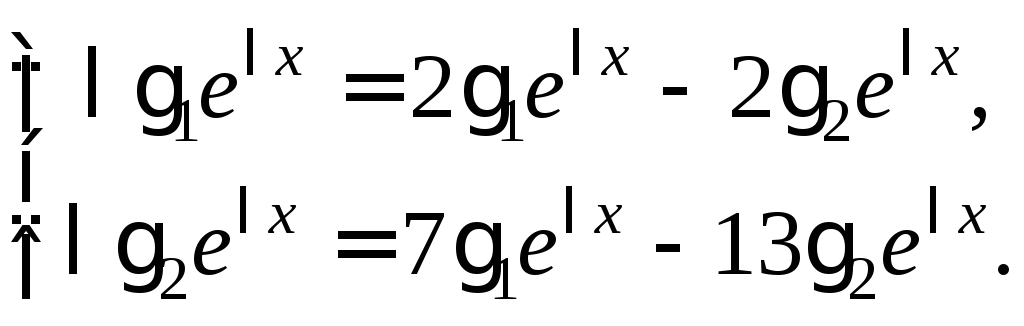
После сокращения на и переноса всех членов в левую часть равенств, получим

(3.27)

Получили однородную систему алгебраических уравнений относительно и, которая имеет ненулевые решения, если определитель равен нулю, т.е.Это уравнение является характеристическим уравнением системы. Раскрывая определитель, имеемилиЭто квадратное уравнение имеет два вещественных различных корняи.

Построим частное решение вида (3.26) для первого корня характеристического уравнения , т.е. и. Запишем систему (3.27) для . Получим

.

Чтобы получить первое ненулевое решение, положим , тогда- первое частное решение.

Построим второе частное решение вида (3.26) для . Запишем для ,систему (3.27):

,

тогда возьмем и получим второе частное решение. Общее решение системы линейных уравнений (3.24) запишется в виде линейной комбинации частных решений, т.е. в виде. Для нашей системы имеем искомое общее решение

. (3.28)

Чтобы найти частное решение, удовлетворяющее начальным условиям (3.25), подставим в (3.28) .

Получим систему решая ее, найдем, тогда искомое частное решение:

Задача 3.3. Найти решение системы дифференциальных уравнений методом исключения (3.29)

Метод исключения заключается в сведении системы дифференциальных уравнений к одному дифференциальному уравнению. В данном случае система второго порядка и получить нужно уравнение второго порядка. Для этого продифференцируем второе уравнение

(3.30).

Подставим в (3.30) , получим , куда подставим из второго уравнения, тогда, т.е.. Получили линейное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнениеимеет корниКорни вещественные различные. Общее решение уравненияимеет вид, т.е.. Выражение длянайдем из второго уравнения системы, где. Учитывая, что, получимили.

Общее решение системы (3.29):