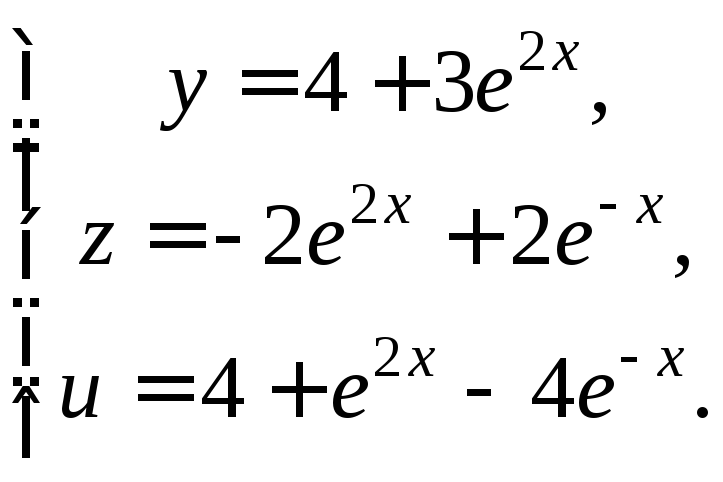3.2. Системы линейных дифференциальных уравнений с постоянными коэффициентами

В рассматриваемой теме Вам предстоит ознакомиться со следующими вопросами:

• Линейные однородные и линейные неоднородные системы.

• Характеристическое уравнение системы.

При необходимости дополнительной информации обращайтесь к [1].

Линейные однородные и линейные неоднородные системы

Важное значение среди нормальных систем дифференциальных уравнений имеют системы вида

(3.10)

где функции инепрерывны на некотором интервале. На основании теоремы существования и единственности решения нормальной системы можно утверждать, что для любого значенияиз и любых чисел у системы (3.10) существует единственное решение которое определено в некоторой окрестности точки и удовлетворяет начальным условиям

Если на интервале функции тождественно равны нулю, то система (3.10) называетсялинейной однородной; в противном случае - линейной неоднородной.

Теория линейных систем (свойства их решений, структура общего решения, специальные методы интегрирования) аналогична теории линейных дифференциальных уравнений -го порядка.

Характеристическое уравнение системы

Рассмотрим подробнее системы линейных однородных дифференциальных уравнений с постоянными коэффициентами. Для простоты записи ограничимся случаем

Итак, рассмотрим систему

(3.11)

где - вещественные числа.

Используя метод Эйлера, будем искать решение системы (3.11) в виде

(3.12)

где - некоторые числа, которые надо подобрать так, чтобы функции (3.12) были бы решением системы (3.11).

Подставив функции (3.12) в систему (3.11), получим (после сокращения на и переноса всех членов в левую часть равенств):

(3.13)

Эта система уравнений служит для определения неизвестных Относительносистема (3.13) является системойлинейных однородных уравнений. Известно, что для того чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ее определитель был равен нулю, т.е. число должно удовлетворять уравнению

(3.14)

Уравнение (3.14) называется характеристическим (вековым) уравнением системы (3.11), а его корни - характеристическими числами системы (3.11). В нашем случае уравнение (3.14) - уравнение третьей степени относительно .

Рассмотрим случай, когда все корни характеристическогоуравнения вещественны и различны. Подставляя поочередно каждый корень вместов систему (3.13) и находя каждый раз ненулевые решения, сможем получить три частных решения системы (3.11):

(3.15)

Можно показать, что линейная комбинация решений (3.15) с произвольными постоянными представляет собою общее решение системы (3.11)

Пример 3.2. Найти частное решение системы уравнений

(3.16)

удовлетворяющее начальным условиям

(3.17)

Вначале обратим внимание на то, что искомые функции в каждом из уравнений системы (3.16) следуют друг за другом в том же порядке, в котором выписаны уравнения, разрешенные относительно

Найдем сначала общее решение системы (3.16), для чего составим ее характеристическое уравнение

Раскрыв определитель, стоящий в левой части, будем иметь

Записав последнее уравнение в виде легко найти его корни, т.е. характеристические числа системы (3.16)

Построим частное решение вида (3.12), соответствующее корню для чего подставим в систему (3.13)Получим

Поскольку достаточно найти одно ненулевое решение этой системы, то, положив найдемПодставляя найденные значения в (3.12), получим первое частное решение системы (3.16)

(3.18)

Построим частное решение вида (3.12), соответствующее корню для чего подставим в систему (3.13)Получим:

Для отыскания одного ненулевого решения этой системы положим Тогда найдемИспользуя формулы (3.12), получим второе частное решение

(3.19)

Для получения третьего частного решения вида (3.12), отвечающего корню положим в системе (3.13)Будем иметь

Из третьего уравнения следует а чтобы найти ненулевое решение последней системы, положимтогда из первого (или второго) уравнения следуетПодставляя найденные значения в (3.12), получим третье частное решение системы (3.16)

(3.20)

Используя частные решения (3.18),(3.19),(3.20), выпишем общее решение системы (3.16)

(3.21)

где - произвольные постоянные.

Для получения частного решения, удовлетворяющего начальным условиям (3.17), положим в равенствах (3.21) и воспользуемся условиями (3.17). Получим систему уравнений для определения значений.

Решив последнюю систему, найдем а тогда частное решение имеет вид