Решение задач

Задача 2.4. Решить уравнение

Составляем характеристическое уравнение для соответствующего однородного уравнения и находим его корниТак как числоявляется простым корнем характеристического уравнения, тоСтепень многочлена в правой части данного уравнения равна единице, и, следовательно, частное решение следует искать в виде

(2.59)

где и - неопределенные коэффициенты. Вычислим и

Подставляя в данное уравнение и сокращая на получим

или

Приравнивая коэффициенты при одинаковых степенях , получим систему двух уравнений

откуда находим Искомое частное решение имеет вид а общим решением заданного уравнения будет

(2.60)

где и- произвольные постоянные.

Задача 2.5. Решить уравнение

(2.61)

Составляем характеристическое уравнение для соответствующего однородного уравнения

(2.62)

и находим его корни По виду выражения (2.57) и правой части данного уравнения находим, что Так как комплексное число не является корнем характеристического уравнения (2.62), то частное решение уравнения (2.61) в соответствии с равенством (2.58), следует искать в виде

где и- неопределенные коэффициенты, означающие многочлены и. Вычислим вначалеи:

Подставив в уравнение (2.61) и сократив на получим

или

Приравнивая коэффициенты при и , получим систему двух уравнений

откуда следует Искомое частное решение имеет вида общим решением уравнения (2.61) будет

где и- произвольные постоянные.

Вопросы для самопроверки по теме 2.3

1. В чем заключается метод Л.Эйлера для построения фундаментальной системы решений линейного однородного уравнения с постоянными коэффициентами?

2. Как найти методом неопределенных коэффициентов частное решение линейного неоднородного уравнения в случаях специального вида правой части уравнения: а) ; б), где- вещественные числа,- многочлены степени?

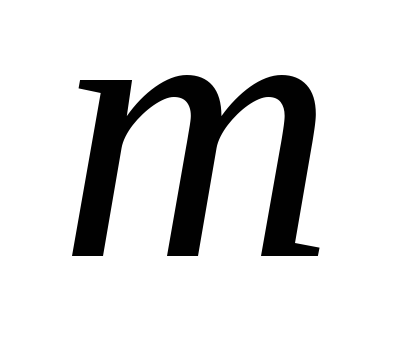Раздел 3. Системы обыкновенных

дифференциальных уравнений

Данный раздел содержит следующие темы:

3.1.Основные понятия.

3.2.Системы линейных дифференциальных уравнений с постоянными коэффициентами.

3.3. Элементы теории устойчивости.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №6. При возникающих затруднениях в ответах обратитесь к [1].

3.1.Основные понятия

В рассматриваемой теме Вам предстоит познакомиться со следующими вопросами:

• Нормальная система дифференциальных уравнений.

• Метод исключения, фазовое пространство.

Нормальная система дифференциальных уравнений

Ранее мы рассматривали обыкновенные дифференциальные уравнения вида

где - независимая переменная, - искомая функция, - заданная функция своих аргументов,a - порядок уравнения.

Однако самые разнообразные задачи науки и техники приводят к необходимости изучения систем дифференциальных уравнений с несколькими неизвестными функциями.

Рассмотрим, например, систему уравнений вида

(3.1)

где - независимая переменная, - неизвестные функции, зависящие от a - заданные функции своих аргументов. Система вида (3.1) называется нормальной системой дифференциальных уравнений.

Можно показать, что любая система уравнений, разрешенных относительно старших производных искомых функций может быть приведена к нормальной системе вида (3.1).

Всякая совокупность функций определенных и непрерывно дифференцируемых на интервале называется решением системы (3.1) в этом интервале, если при подстановке их в уравнения системы они обращают их в тождества, справедливые при всех из . Процесс нахождения решений системы (3.1) называетсяинтегрированием (решением) этой системы.