1) 2)3)

Каждое из данных уравнений является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Составим характеристическое уравнение для каждого уравнения:

1) 2)3)

Найдем корни каждого характеристического уравнения

1)

2)

3)

Общие решения при этом будут иметь вид:

1) 2) 3)

где и- произвольные постоянные.

Перейдем теперь к построению фундаментальной системы решений для уравнения -го порядка (2.45). Проводя для уравнения (2.45) рассуждения аналогичные проведенным для уравнения второго порядка (2.46), легко убедиться, что вопрос об отыскании его фундаментальной системы сводится к решению уравнения

(2.51)

которое называется характеристическим уравнением уравнения (2.45) и которое составляется по тому же правилу, что и характеристическое уравнение для уравнения второго порядка (2.46), а именно: производные от искомой функции заменяются соответствующими степенями (искомая функция рассматривается как производная нулевого порядка). Корни уравнения (2.51) называютсяхарактеристическими числами уравнения (2.45).

Сформулируем общее правило решения линейного однородного уравнения -го порядка:

1) Составляем характеристическое уравнение:

2) Находим корни характеристического уравнения

3) Находим частные линейно независимые решения уравнения (2.45), руководствуясь тем, что:

а) каждому действительному корню кратностисоответствует линейно независимых частных решений

б) каждой паре комплексных сопряженных корней и кратности соответствует линейно независимых частных решений

Всего таких частных решений будет ровно , причем можно показать, что они линейно независимы на всей числовой оси.

4) Составляем линейную комбинацию найденных решений с произвольными коэффициентами, которая и будет общим решением уравнения (2.45) в области

Пример 2.8. Решить уравнение

Составим характеристическое уравнение

Это уравнение имеет три простых корня Вещественному корнюсоответствует частное решение а паре комплексных сопряженных корней исоответствует два линейно независимых частных решения

Общее решение будет иметь вид

где - произвольные постоянные.

Линейные неоднородные дифференциальные уравнения -го порядка.Метод неопределенных коэффициентов

Перейдем теперь к рассмотрению линейных неоднородных уравнений

-го порядка

(2.52)

где - вещественные числа, а функциянепрерывна в некотором промежутке

Ранее было показано, что общее решение уравнения (2.52) может быть представлено в виде суммы общего решения соответствующего однородного уравнения и произвольного частного решения уравнения (2.52). Правила отыскания общего решения однородного уравнения, соответствующего уравнению (2.52) были изложены выше. Для отыскания частного решения уравнения (2.52) можно использовать метод Лагранжа вариации произвольных постоянных. Но его применение часто приводит к необходимости производить довольно сложные вычисления. Однако, для некоторых случаев, когда правая часть имеетспециальный вид, удается найти частное решение уравнения (2.52) без квадратур с помощью метода неопределенных коэффициентов.

Метод неопределенных коэффициентов состоит в том, что частное решение неоднородного уравнения (2.52) ищется в виде, определяемом видом правой части уравнения. При этом сначала задается вид частного решения с неопределенными коэффициентами, а затем эти коэффициенты определяются после подстановки этого решения в левую часть уравнения (2.52) и приравнивания коэффициентов при одинаковых степенях в левой и правой частях полученного равенства.

1) Рассмотрим сначала случай, когда правая часть уравнения (2.52) имеет вид

(2.53)

где - вещественное число, а - многочлен степени .

В этом случае частное решение уравнения (2.52) следует искать в виде

(2.54)

где - многочлен степени с неопределенными коэффициентами, а - кратность числа как корня характеристического уравнения однородного уравнения соответствующего уравнению (2.52) (если не является корнем указанного характеристического уравнения, то считается равным нулю).

Пример 2.9. Решить уравнение . (2.55)

Здесь - многочлен второй степени,, т.е..

Составляем характеристическое уравнение для соответствующего однородного уравнения и находим его корни

Частное решение, соответствующее правой части, ищем в виде (2.54), т.е.

(2.56)

Здесь - многочлен второй степени () с неопределенными коэффициентами и, так как корни характеристического уравнения;, не совпадают с числом(оно не является корнем характеристического уравнения), то.

Чтобы найти числа , подставим (2.56) в уравнение (2.55), предварительно найдяи

; .

Получим:

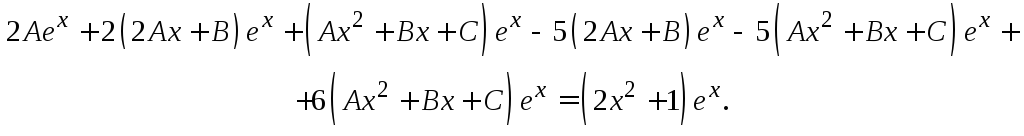
Разделив обе части уравнения на , имеем:

или .

Приравнивая коэффициенты при одинаковых степенях в левой и правой части тождества, получим систему уравнений

, откуда Таким образом,.

Пример 2.10. Если же требуется решить уравнение , то опять правая часть имеет вид, где- многочлен нулевой степени;и совпадает с одним из корней характеристического уравнения. Тогда в уравнении (2.54), а- неизвестное число и решениеищем в виде. Находим производные,и подставляем их в уравнение. Получим.

Сокращая на , имееми в этом случае.

2) Рассмотрим теперь случай, когда правая часть уравнения (2.52) имеет вид

(2.57)

где и -любые вещественные числа, а и- многочлены от , старшая степень которых равна.

В этом случае частное решение уравнения (2.52) следует искать в виде

(2.58)

где и- многочлены степени с неопределенными коэффициентами, а- кратность комплексного числа как корня характеристического уравнения однородного уравнения соответствующего уравнению (2.52) (еслине является корнем указанного характеристического уравнения, тосчитается равным нулю).

Пример 2.11. Найти частное решение уравнения .

Правая часть уравнения имеет вид (2.57), где . Тогда,не является корнем характеристического уравнения, т.е.. Частное решение имеет вид, где,ипросто постоянные (или многочлены нулевой степени).

Итак .

Находим производные ;и, подставляя,в уравнение, получим:

или . Приравнивая коэффициенты приив правой и левой части, получим, откуда.

Таким образом, .