Вопросы для самопроверки по теме 2.2

1. Какое дифференциальное уравнение называется линейным дифференциальным уравнением -го порядка?

2. Какое линейное дифференциальное уравнение называется однородным?

3. Какими свойствами обладают решения однородного дифференциального уравнения?

4. Дайте определения линейно зависимой и линейно независимой на промежутке систем функций.

5. Какое условие является необходимым и достаточным, чтобы решенийлинейного однородного дифференциального уравнения были линейно независимы на промежутке?

6. Что называется фундаментальной системой решений линейного однородного уравнения -го порядка?

7. Сформулируйте теоремы о структуре общего решения линейного однородного и неоднородного уравнений.

2.3. Линейные дифференциальные уравнения с постоянными коэффициентами

В рассматриваемой теме Вам предстоит ознакомиться со следующими вопросами:

• Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера.

• Линейные неоднородные дифференциальные уравнения -го порядка.Метод неопределенных коэффициентов.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №5. При возникающих затруднениях в ответах обратитесь к [1].

Студентам очно-заочной и заочной форм обучения надо решить одну задачу из контрольной работы № 5 под номерами 21-30 в соответствии со своим вариантом.

Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера

Рассмотрим линейное однородное уравнение -го порядка

(2.45)

где коэффициенты постоянны.

Л.Эйлер показал, что для уравнения (2.45) всегда можно построить фундаментальную систему решений, состоящую из элементарных функций, и, следовательно, оно всегда интегрируется в элементарных функциях. Ниже это утверждение доказывается для уравнения второго порядка, и формулируются окончательные результаты для уравнения -го порядка.

Рассмотрим уравнение второго порядка

(2.46)

где и- любые вещественные числа.

Следуя Л.Эйлеру, будем искать решения уравнения (2.46) в виде

(2.47)

где - некоторое число, которое постараемся подобрать так, чтобы функция (2.47) удовлетворяла уравнению (2.46).

Так как ато, подставив (2.47) в левую часть уравнения (2.46), получим

Множитель отличен от нуля, следовательно, числодолжно быть корнем уравнения

(2.48)

Это уравнение называется характеристическим уравнением уравнения (2.46), а его корни - характеристическими числами уравнения (2.46).

Заметим, что характеристическое уравнение (2.48) может быть составлено по данному уравнению (2.46), если заменить в нем исоответственно наи 1.

Уравнение (2.48) является квадратным и, следовательно, имеет два корня, которые мы обозначим через и..

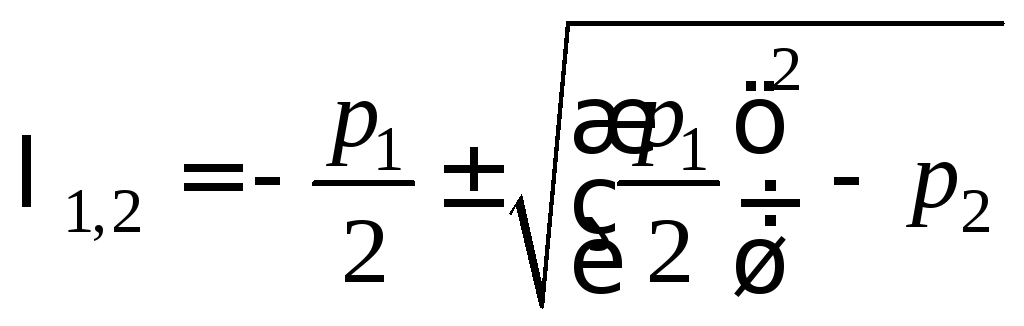Структура фундаментальной системы решений зависит от вида корней характеристического уравнения.

Возможен один из трех случаев:

1) - вещественные и различные,

2) - вещественные и равные,

3) - комплексные,

Перейдем к построению общего решения уравнения (2.46) в каждом из этих случаев.

1) Подставляя в формулу (2.47) вместо корнииполучим два частных решения уравнения (2.46)

(2.49)

Эти решения, очевидно, линейно независимы, так как их отношение

отлично от постоянной. Кроме того, в линейной независимости решений (2.49) можно убедиться с помощью определителя Вронского. Имеем

Итак, решения (2.49) образуют фундаментальную систему решений уравнения (2.46) и, следовательно, его общее решение можно записать в виде

где и - произвольные постоянные.

2) В этом случае дискриминант квадратного уравнения (2.48) равен нулю, т.е.

, (2.50)

и, следовательно,

Одно решение получается на основании предыдущих рассуждений: это функция

Теперь возникает вопрос об отыскании второго решения уравнения (2.46), линейно независимого с Непосредственной подстановкой в уравнение (2.46) можно убедиться в том, что функция является решением уравнения (2.46), причем решениелинейно независимо с решениеми, следовательно, они образуют фундаментальную систему решений уравнения (2.46), а его общее решение имеет вид

где и - произвольные постоянные.

Прежде чем переходить к рассмотрению третьего случая, остановимся на понятии комплексного решения уравнения (2.46).

Пусть в интервале даны две вещественные дважды непрерывно дифференцируемые функциииаргумента. Комплексная функцияназываетсякомплексным решением линейного однородного уравнения (2.46) в интервале , если всюду в этом интервале имеет место тождество

Нетрудно убедиться, что последнее тождество можно записать в виде которое, равносильно двум

Отсюда следует, что вещественная и мнимая части комплексного решения линейного однородного уравнения (2.46) являются вещественными решениями этого уравнения.

Наконец, для любых вещественных чисел иопределим комплексную показательную функцию действительного аргументапри помощи равенства

Последнюю формулу называют формулой Эйлера.

3) Так как числа и вещественные, то комплексные корнииявляются сопряженными и для них можем написать

Корню будет соответствовать комплексное решениекоторое с помощью формулы Эйлера может быть записано в виде

Поскольку вещественная и мнимая части комплексного решения сами являются вещественными решениями, то получаем два частных решения уравнения (2.46)

в чем можно убедиться и непосредственной подстановкой их в уравнение (2.46).

Легко видеть, что эти решения линейно независимы на всей числовой оси (их отношение отлично от постоянной). Аналогично, корню соответствуют вещественные частные решения которые линейно зависимы с решениями, соответствующими корню

Итак, паре комплексных сопряженных корней соответствуетдва линейно независимых частных решения и, следовательно, общее решение уравнения (2.46) в этом случае имеет вид

где и- произвольные постоянные.

Пример 2.7. Найти общее решение для каждого уравнения: