Построение логических схем по аналитическим выражениям функций

Логической схемой (ЛС) называется схема, составленная из ЛЭ путем соединения выходов одних ЛЭ со входами других.

Построение логических схем по аналитическим выражениям функций другими словами называется реализацией логических функций.

Существует ряд базисов, из числа которых были рассмотрены И, ИЛИ, НЕ; И—НЕ и ИЛИ—НЕ. В каждом базисе могут быть реализованы любые логические функции.

Схема, которая получается на основании логического выражения, носит название комбинационной схемой.

При переходе от логического выражения к логической схеме элементы, выполняющие в выражении те или иные операции, располагаются в схеме, начиная от входов.

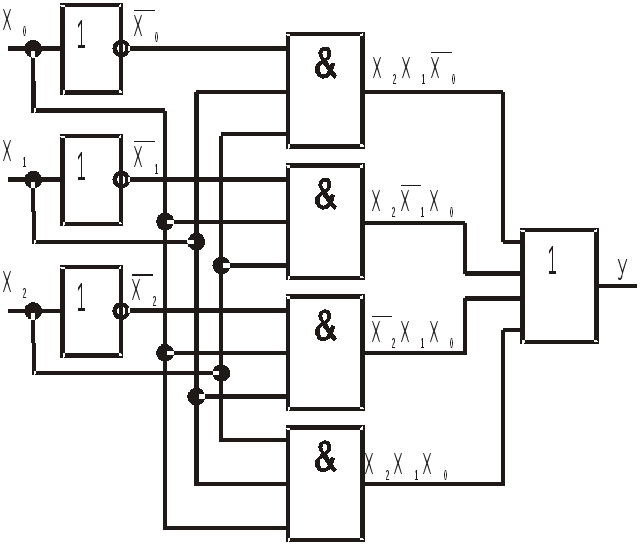
Рассмотрим принцип построения логических схем на примере выражения (1.1) для мажоритарной функции в СДНФ, полученной ранее:

.

На логической схеме сначала изображаются 3 инвертора, для отрицания входных переменных, затем 3 элемента И на три входа каждый и наконец 1 элемент ИЛИ на четыре входа. После размещения элементов изображаются электрические связи (проводники), соединяющие входные переменных и выходные сигналы одних элементов со входами других согласно логическому выражению.

Построение ЛС основано на следующих правилах:

1. Выход ЛЭ можно подсоединять ко входам нескольких ЛЭ;

2. На входы ЛЭ можно подавать сигналы, представляющие собой константы 0 и 1.

3. Выходы ЛЭ нельзя соединять вместе;

4. Выходы ЛЭ нельзя подключать к собственным входам.

Логическая схема для рассматриваемой функции в СДНФ реализована в базисе И, ИЛИ, НЕ и изображена на рис. 1.13.

Аналогично строится логическая схема для этой же функции после её минимизации по аналитической записи в МДНФ (1.4):

Такая логическая схема в булевом базисе приведена на рис.1.14. Сравнив две построенные схемы можно видеть что последняя схема содержит в два раза меньшее количество ЛЭ, которые имеют меньшее число входов.

Можно построить логическую схему в булевом базисе для этой же функции после её минимизации по аналитической записи в МКНФ (1.5),

,

которая представлена на рис. 1.15.

Часто необходимо построить схему из однотипных ЛЭ. Для этого требуется реализовать схему в базисе И–НЕ или в базисе ИЛИ–НЕ. Переход к другому базису осуществляется путем выполнения тождественных преобразований исходных выражений в формах СДНФ, МДНФ или СКНФ, МКНФ.

Для построения схемы в базисе И–НЕ можно преобразовать аналитическую запись функции в МДНФ (1.4) путем её двойного инвертирования и применения закона Де Моргана:

.

Логическая схема в базисе И–НЕ приведена на рис.1.16.

Для построения схемы в базисе ИЛИ–НЕ можно преобразовать аналитическую запись функции в МКНФ (1.5) также путем её двойного инвертирования и применения закона Де Моргана:

Логическая схема в базисе ИЛИ–НЕ приведена на рис.1.17.

Далее рассматривается несколько простых логических функций, реализуемых элементами рассмотренных базисов.

Элемент «Сравнение». На выходе такого элемента должна быть логическая 1, если на входах одновременно присутствуют одинаковые логические переменные (единицы или нули).

Легко установить, что при равнозначности переменных х₁ и х₀ конъюнкции их прямых или инверсных значений равны единице, т. е. функция рассматриваемого элемента выразится в базисе как

Используя теорему де Моргана, представим эту функцию в базисе И—НЕ:

На рис. 1.17, а, б приведены логические схемы элемента «Сравнение» на ЛЭ базисов И, ИЛИ, НЕ и И—НЕ соответственно. Условное графическое изображение элемента дано на рис. 1.18, в.

Элемент «Исключающее ИЛИ». На выходе такого элемента должна быть логическая 1, если на входах присутствуют неравнозначные логические переменные:

у=1, если х₁=1, x₀=0 или ;х₁=0, x₀= 1.

Исходя из самого определения, легко записать логическую функцию: конъюнкции неравнозначных переменных должны быть равны единице, т. е.

.

Применяя теорему де Моргана, запишем эту функцию в базисе И—НЕ:

,

где правая часть выражения дополнительно дважды инвертирована.

Функциональные схемы рассматриваемого элемента в соответствии с выражениями приведены на рис. 1.18, а, б. Условное обозначение элемента «Неравнозначность» дано на рис. 1.18,в.

Элемент «исключающее ИЛИ» иначе называют сумматором по модулю два: сумма двоичных цифр дает в результате 1; если одна из них 1, а другая — 0; эта сумма равна 0, если обе цифры одинаковы – 0 или 1.