Химия2013 / Раздача ИЗз-09Коллоидная / CollCh / Lec / Lecture4

Значения порогов коагуляции (обозначим их cб′, cб′′ и cб′′),341 вызываемой электролитами с зарядами противоионов 1, 2 и 3 соответственно по теории ДЛФО (4.68) относятся как

где сэл – концентрация электролита, моль/м3, V – объем электролита м3, Vз – объем золя, вызывающий коагуляцию, м3.

Первое правило Шульце—Гарди формулируется следующим образом:чем выше заряд коагулирующего иона, тем меньше не-

го нужно для коагуляции.

Исходя из этого в литературе часто выражение (4.69) назы-

вают правилом Шульце—Гарди. хотя экспериментальная зави-

симость порога коагуляции от заряда иона несколько меньше, чем z6

Последнее объясняется, по-видимому, увеличением роли специфической адсорбции с ростом заряда ионов. Таким образом, даже упрощенные варианты теории ДЛФО позволяют приближенно, но качественно правильно описать основные экспериментальные закономерности коагуляции электролитами.

Приближенность соотношений теории ДЛФО заключается еще в том, что в них не учтена природа противоионов с одинаковым зарядом.

Второе правило Шульце—Гарди формулируется следую-

щим образом: для ионов одинакового заряда порог коагуляции

тем ниже, чем выше порядковый номер элемента, образующеего этот ион.

Коагулирующая способность электролита определяется положением иона в лиотропном ряду.

342

Многозарядные ионы, обладающие способностью перезаряжать поверхность частицы и изменять знак ζ- потенуиала, образуют неправильные ряды.

Лиотропные ряды характеризуют сродство ионов к растворителю. Таким образом, чем ионы более лиофобны, тем большим коагулирующим действием они обладают. Этот факт можно объяснить увеличением специфической адсорбции ионов этих рядов. Следует также учитывать вклад в коагулирующее действие противоионов, находящихся в диффузной части двойного электрического слоя. Чем противоион гидрофильнее, тем он обеспечивает большее взаимодействие частиц со средой и тем система более устойчива. Еще большее влияние на устойчивость (или коагуляцию) оказывают, органические ионы, которые, обладая большой поверхностной активностью, могут нейтрализовать заряд в адсорбционном слое.

Коагулирующее действие смесей электролитов часто бывает неаддитивным.

Иногда для начала коагуляции требуется смесь электролитов, в большем количестве, чем одного из них. Такое явление называют антагонизмом электролитов.

Если же смесь электролитов действует эффективнее одного электролита, то проявляется синергизм электролитов. Очень сильное влияние на устойчивость и коагуляцию дисперсных систем оказывают электролиты, вступающие в химическое взаимодействие с противоионами мицелл или стабилизирующим электролитом.

Рассмотренные выше количественные закономерности коагуляции электролитами относятся в основном к порогу быстрой коагуляции, когда потенциальный барьер равен нулю или фактор устойчивости W (коэффициент стабильности) равен единице.

В соответствии с теорией медленной коагуляции, разрабо-

танной Н. А. Фуксом, учитывающей только электростатическое отталкивание, фактор устойчивости в первом приближении определяется уравнением

343

Сравнение (4.70) с определением фактора устойчивости

(4.12) показывает, что стерический множитель P связан с величиной χ, обратной толщине диффузного слоя, и радиусом час-

Теория медленной коагуляции предсказывает линейную зависимость (в логарифмических координатах) фактора устойчивости от концентрации электролита, что подтверждается экспериментально.

Защита коллоидных частиц. Сенсибилизация. Гетерокоагуляция и гетероадагуляция

Коллоидной защитой называется повышение агрегативной устойчивости золя путем введения в него ВМС.

Защитное действие ВМС связано с образованием на поверхности коллоидных частиц определенного адсорбционного слоя.

Для характеристики защитного действия ВМС Зигмонди предложил использовать золотое число.

Золотое число – это количество миллиграммов ВМС, которое надо добавить к 10 см3 0,0006%-го красного золя золота, чтобы предотвратить его посинение при добавлении к нему 1 см3 10%-го раствора NaCl.

Иногда для характеристики защитного действия ВМС вместо золя золота используют коллоидные растворы серебра (серебряное число), гидроксида железа (железное число) и др.

В некоторых случаях введение в коллоидную систему очень малых количеств ВМС приводит не к защите, а к снижению ус-

тойчивости.

Снижение порога коагуляции золя при добавлении в него ВМС называется сенсибилизацией.

344

Особенно характерна сенсибилизация для линейных макромолекул, несущих на обоих концах цепи. Длинная молекула полимера присоединяется двумя концами к двум разным частицам дисперсной фазы, скрепляет их углеводородным мостиком. Этот вид коагуляции, называемый флокуляцией, приводит к образованию рыхлых хлопьевидных частиц – флоккул.

Гетерокоагуляцией называется слипание разнородных частиц.

Один из типичных случаев гетерокоагуляции – взаимная коагуляция – слипание разноименно заряженных частиц, кото-

рое происходит за счет электростатических сил притяжения. Может происходить и тогда, когда частицы золя несут заряды одного знака.

Гетероадагуляция (гетерогенная адгезионная коагуляция)

– прилипание частиц дисперсной фазы к вводимой в систему чужеродной поверхности. Одна из причин потери устойчивости дисперсных систем в присутствии чужеродной поверхности – адсорбция стабилизатора на этой поверхности и уменьшение его концентрации в коллоидной системе.

СТРУКТУРНО-МЕХАНИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ

Основные понятия и идеальные законы реологии

Под структурой тел обычно понимают пространственное взаимное расположение составных частей тела: атомов, молекул, мелких частиц.

Структура разбавленных агрегативно устойчивых дисперсных систем по ряду свойств очень похожа на структуру истинных растворов.

Основное отличие состоит в том, что в дисперсных (гетерогенных) системах частицы дисперсной фазы и молекулы дисперсионной среды сильно различаются по размерам.

345

Увеличение концентрации дисперсной фазы приводит к взаимодействию ее частиц подобному ассоциации молекул и ионов в истинных растворах. Изменение свойств дисперсных систем с ростом концентрации происходит постепенно до тех пор, пока не наступит коагуляция частиц. В коллоидной химии понятия структуры и структурообразования принято связывать именно

с коагуляцией, в процессе которой происходит образование пространственной сетки из частиц дисперсной фазы с резким увеличением прочности системы.

Таким образом, структурообразование в свободнодисперсных системах есть результат потери их агрегативной устойчивости. В результате структурообразования свободнодисперсная система может перейти в связнодисперсную систему.

Появление и характер структур, как правило, определяют по механическим свойствам систем, важнейшими из которых яв-

ляются

вязкость,

упругость,

пластичность,

прочность.

Так как эти свойства непосредственно связаны со строением, структурой тел, то их часто называют структурно-

механическими.

Изменения структурно-механических свойств систем обусловлены взаимодействиями частиц со средой и между собой, исследовать которые позволяют методы реологии — науки о дефор-

мациях и течении материальных систем. Поэтому структурно

механические свойства часто называют реологическими

Реология изучает механические свойства систем через деформации под действием внешних напряжений.

346

В коллоидной химии методы реологии используют для исследования структуры и описания вязкотекучих свойств дисперсных систем.

Термин деформация означает относительное смещение точек системы, при котором не нарушается ее сплошность.

Деформацию делят на упругую и остаточную.

Упругая деформация исчезает после снятия нагрузки (напряжения).

Остаточная деформация необратима, изменения в системе остаются и после снятия нагрузки.

Остаточная деформация, при которой не происходит разрушения тела, называется пластической.

Среди упругих деформаций различают

объемные (растяжение, сжатие),

сдвиговые и

деформации кручения.

Они характеризуются количественно относительными (безразмерными) величинами.

Например,

при одномерном деформировании растяжение характеризуется относительным удлинением:

где l0 и l — длина тела до и после растяжения соответственно; ∆l — абсолютное удлинение.

Деформация сдвига определяется относительным сдвигом (рис. 63) под действием напряжения Р:

где x — смещение верхнего слоя; у — высота, на протяжении которой происходит смещение; α – угол сдвига.

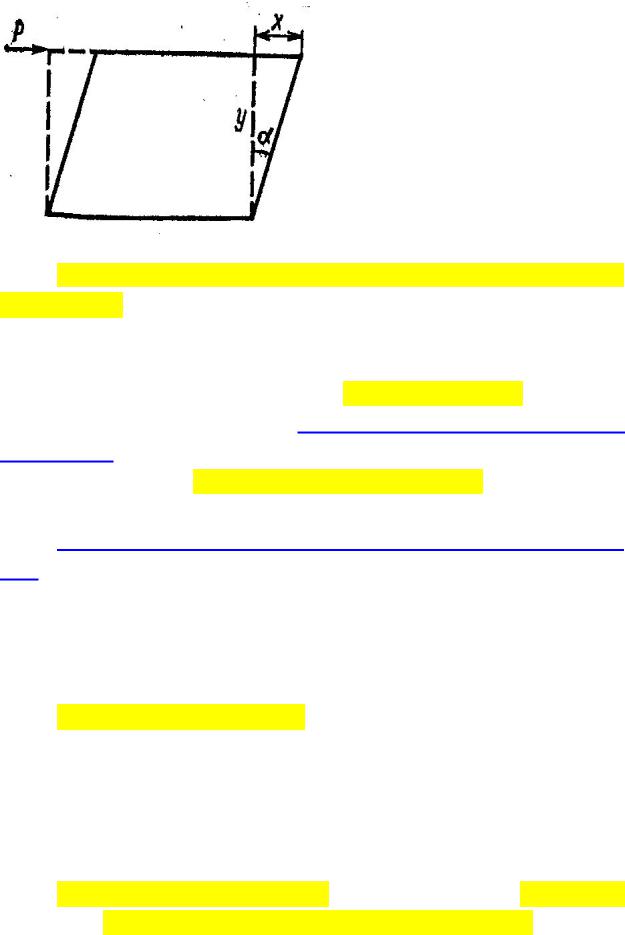
347

Рис. 63. Схематическое изображение деформации сдвига

Жидкости и газы деформируются при наложении минимальных нагрузок. Под действием разности давлений они текут.

Течение является одним из видов деформации, когда величина деформации непрерывно увеличивается под действием постоянного давления (нагрузки). В отличие от газов жидкости при течении не сжимаются, и их плотность остается практически постоянной.

Напряжение, вызывающее деформацию тела, определяется

отношением силы к площади, на которую она действует.

Действующая сила может быть разложена на две составляю-

щие:

¾нормальную, направленную перпендикулярно к поверхности тела, и

¾тангенциальную (касательную), направленную по каса-

тельной к этой поверхности. Соответственно различают два вида напряжений:

¾нормальные и

¾тангенциальные,

которым отвечают два основных вида деформаций:

¾растяжение (или сжатие) и

¾сдвиг.

Остальные виды деформации можно представить с помощью различных комбинаций этих основных видов деформаций.

348

Единицей напряжения в СИ является Па (паскаль). Примером соответствия характера (вида) деформации виду

напряжения является первая аксиома реологии: при всестороннем

равномерном (изотропном) сжатии все материальные системы ведут себя одинаково — как идеальные упругие тела. Это озна-

чает, что в таких разных по структуре телах, как металл, смола, вода, кислород-газ и др., изотропное сжатие вызывает только упругую деформацию, а именно уменьшаются размеры системы при со-

хранении ее формы и увеличивается плотность. При снятии на-

грузки все параметры тела принимают первоначальные значе-

ния. Отсюда следует, что изотропное сжатие не позволяет выявить качественные различия в структуре тел.

Вместе с тем любая материальная система обладает всеми реологическими свойствами (вторая аксиома реологии). Основ-

ными из них являются

упругость,

пластичность,

вязкость и

прочность.

Все эти свойства проявляются при сдвиговой деформации, которая поэтому считается наиболее важной в реологических исследованиях.

Таким образом, характер и величина деформации зависят от свойств материала тела, его формы и способа приложения внешних сил.

В реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат три основных идеальных закона, связывающих напряжение с деформацией.

Им соответствуют три элементарные модели (элемента) идеализированных материалов, отвечающих основным реологи-

ческим характеристикам (упругость, пластичность, вязкость):

349

идеально упругое тело Гука,

идеально пластическое тело Сен-Венана — Кулона и идеально вязкое тело Ньютона (ньютоновская

жидкость).

Идеально упругое тело Гука представляют в виде спиральной пружины (рис. 64).

Рис. 64. Модель идеально упругого тела Гука (а) и зависимость деформации этого тела от напряжения (б)

В соответствии с законом Гука деформация в упругом теле пропорциональна напряжению сдвига:

где Е — коэффициент пропорциональности (или модуль Юнга).

Модуль Юнга Е является характеристикой материала (его

структуры), количественно отражающей его упругие свойства (жесткость).

Из уравнения (4.74) следует, что единицей измерения модуля Юнга является паскаль (СИ) (γ – безразмерная величина).

Из рис. 64 следует, что модуль Юнга можно определить по тангенсу угла наклона α прямой к оси γ .

После снятия нагрузки идеально упругое тело Гука мгновенно переходит в первоначальное состояние (форму). Деформации в упругих телах происходят со скоростью распространения звука в них.

Идеально вязкое тело Ньютона изображают в виде поршня с отверстиями, помещенного в цилиндр с жидкостью (рис. 65).

350

Рис. 65. Модель идеально вязкой жидкости Ньютона (а) и зависимость скорости деформации этой жидкости от напряжения (б)

Идеально вязкая жидкость течет в соответствии с законом Ньютона. Согласно этому закону напряжение сдвига при ламинарном течении жидкости с вязкостью η пропорционально

При плоскопараллельном движении двух слоев жидкости происходит сдвиг одного слоя относительно другого.

Если скорость движения слоев жидкости обозначить через

dx / dτ и учесть, что координата у и время τ являются независи-

мыми переменными, то с помощью изменения порядка дифференцирования можно получить следующее соотношение:

где γ = ddτγ — скорость деформации сдвига.

Таким образом, закон Ньютона можно сформулировать еще следующим образом — напряжение сдвига пропорционально

скорости деформации:

Реологические свойства идеальных жидкостей однозначно характеризуются вязкостью.

Ее определение дается уравнениями (4.75)и (4.77). График зависимости γ = f (P) представляет собой прямую, выходящую из

начала координат, тангенс угла наклона этой прямой к оси γ