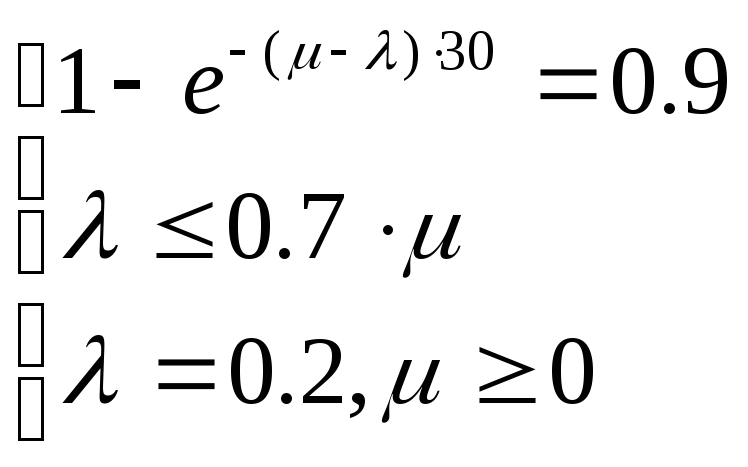23

Моделирование компьютерной сети

Моделирование компьютерной сети является средством системного анализа и должно базироваться на системном подходе.

Основные положения системного анализа

Современная методология исследований рассматривает любой объект как систему. Под системой будем понимать определенное во времени и пространстве множество элементов с известными свойствами и упорядоченными связями между элементами, ориентированными на выполнение главной задачи данного множества.

С системой связан целый ряд понятий, таких как целостность, сложность, структура, цель, подсистема, элемент, свойства, связь, состояние, внешняя среда.

Целостность устанавливает, что познание системы достигается через единство изучения всех ее элементов и поэтому система ни коем случае не должна рассматриваться как их простая сумма. Вместе с тем при анализе систем допускается самостоятельное изучение ее отдельных частей (декомпозиция) при условии их функциональной независимости .

Сложность предписывает учитывать при изучении системы влияние на нее как внешней среды, так и внутренних факторов.

Структура отражает наиболее существенные взаимоотношения между элементами системы, которые обеспечивают существование системы и ее основные свойства и мало меняются от происходящих в системе изменений. Структура системы зависит от глубины отображения объекта, от цели созданий системы, и одна и та же система может быть представлена несколькими структурами.

Цель – желаемое состояние системы. Оценка степени достижения системой поставленной цели производится через критерии цели, которые определяют соответствие состояния системы поставленной цели.

Подсистема – это относительно независимая часть системы, включающая совокупность взаимосвязанных элементов.

Элемент представляет собой условно неделимую часть системы. Степень детализации системы через подсистемы и элементы определяется целями исследования. Подсистема и элемент могут выполнять собственные цели и задачи, однако их функционирование всегда направлено на выполнение главной цели (задачи) системы.

Теоретические основы моделирования лвс

Основное требование к ЛВС – это обеспечение всем пользователям доступа к разделяемым ресурсам сети с заданным качеством обслуживания (QoS – Quality of Service). Одним из основных критериев качества обслуживания является производительность. В качестве показателей производительности используются время реакции, пропускная способность и задержка передачи. Время реакции – это интервал времени между возникновением запроса пользователя к сетевой службе и получением ответа. Время реакции зависит от загруженности сегментов среды передачи и активного сетевого оборудования (коммутаторов, маршрутизаторов, серверов). Пропускная способность – это объем данных, передаваемых в единицу времени (бит/с, пакетов/с). Пропускная способность составного пути в сети определяется самым медленным элементом (как правило, это маршрутизатор). Задержка передачи – это интервал времени между моментом поступления пакета на вход сетевого устройства и моментом появления его на выходе устройства.

Для оптимизации производительности ЛВС используют методы и средства измерения, анализа и моделирования. Клиент-серверная архитектура и распределенная обработка данных в ЛВС усложняют задачи моделирования.

Аналитическое моделирование ЛВС основано на использовании моделей систем массового обслуживания (СМО) [9, 10] и, как правило, связано со значительными упрощениями. Тем не менее результаты аналитического исследования могут быть очень ценными, даже если они не учитывают всех деталей реальной ЛВС. Такие модели позволяют достаточно быстро получить приближенную инженерную оценку влияния характеристик оборудования и программного обеспечения на показатели производительности ЛВС.

Модель ЛВС строится из отдельных блоков, каждый из которых представляет один узел или канал передачи ЛВС. Блок состоит из буферного накопителя пакетов и обслуживающего элемента (рис.1). На вход блока поступает поток пакетов, характеризуемый функцией распределения интервалов времени между моментами поступления пакетов A(t). Интенсивность  входного потока пакетов – это среднее число пакетов, поступающих на вход блока в единицу времени. Обратная величина 1/ – это среднее значение интервала между моментами поступления пакетов, которое о пределяется интегралом

И нтенсивность обслуживания блока – это  среднее число обрабатываемых пакетов в единицу времени. Обратная величина 1/ – это среднее значение длительности обслуживания пакета, которое определяется интегралом

где B(t) – функция распределения длительности обслуживания. Отношение  =  /  называется коэффициентом загрузки блока. Реальный блок имеет буфер ограниченной емкости r (см. рис.2,б). Идеализированный модуль может иметь неограниченный по емкости буфер (см. рис.2,а).

Блок M/M/1. Рассмотрим самую простую модель типа M/M/1 (один обслуживающий элемент, неограниченная емкость буфера, экспоненциальные законы распределения интервалов времени между моментами поступления пакетов и времени обслуживания, дисциплина обслуживания FIFO) для блока, изображенного на рис.1,а. В этом случае A(t)=1– e^{– t}, B(t)=1–e^{– t}, среднее время задержки пакета в блоке

T = 1 / ( –),

(1)

а среднее число пакетов в блоке (в очереди и в процессе передачи)

L =  / ( –).

(2)

Среднее время ожидания в очереди W = T – (1/), а среднее число пакетов в очереди L_W = L – .

Б лок M/G/1. Эта модель отличается от модели типа M/M/1 только тем, что распределение времени обслуживания B(t) может быть произвольном. Рассмотрим случай, когда распределение B(t) задается для блока двумя параметрами: интенсивностью обслуживания  и дисперсией времени обслуживания

Тогда среднее время нахождения пакета в очереди W = (1 + v²) W^П, где W^П = (/2)(1–)^–1 – время нахождения пакета в очереди при постоянной длительности обслуживания; v² = ² D – квадрат коэффициента вариации времени обслуживания. Для постоянного времени обслуживания v=0, а для экспоненциального распределения времени обслуживания v=1. Для модели M/G/1 оценка времени пребывания пакета в блоке T = W + (1/), длины очереди в буфере L_W =W и общего числа пакетов в блоке L = L_W + .

Блоки M/M/1/r и M/G/1/r. Модель типа M/G/1/r для блока, изображенного на рис.1,б, отличается от модели M/G/1 тем, что емкость буфера ограничена величиной r (предполагается, что обрабатываемый пакет находится также в буфере). Эта модель характеризуется вероятностью потери пакета (отказа в обслуживании) [10]

PОТК  (1–) (r,v) /(1–(r,v)+1),

(3)

где (r,)=2r/(1+²), причем   коэффициент вариации. Абсолютная пропускная способность блока M/G/1/r

_АБС= (1– P_ОТК).

При =1 формула дает точное значение P_ОТК для экспоненциального распределения B(t), т.е. для блоков M/M/1/r.

Сеть блоков M/M/1. Модель ЛВС можно представить в виде сети блоков (сети массового обслуживания – СеМО [8]), причем многие блоки содержат буферы. Простые аналитические формулы можно получить для открытой сети блоков M/M/1, пример которой представлен на рис.2.

В этой сети, состоящей из трех блоков, три входных потока пакетов, имеющих интенсивности ₁, ₂ и ₃ соответственно. Требуется оценить среднюю задержку пакетов для каждого потока. Очереди в этой сети можно рассматривать по отдельности [9], причем число пакетов в блоке j=1…3 оценивается по формуле (1), а именно

L_j = _j / (_j – _j).

Интенсивность _j потока на входе каждого блока равна сумме интенсивностей элементарных потоков, поступающих на блок в соответствии с рис.3:

₁ = ₁ + ₂, ₂ = ₁ + ₂ + ₃, ₃ = ₂ + ₃.

Можно показать [9], что средняя задержка пакета в сети

(4)

де n – число блоков в системе;  – сумма интенсивностей всех потоков, входящих в систему. Для отдельного потока i средняя задержка пакета в сети

,

где J_i – подмножество блоков, участвующих в обработке потока i. В рассматриваемом примере J₁={1, 2, 3}, J₂={1, 2} и J₃={2, 3}.

Формула (4) верна при следующих предположениях.

 Закон распределения интервалов времени между моментами поступления пакетов A(t) для отдельных потоков экспоненциальный, причем потоки являются независимыми процессами. Это предположение может быть выполнено на практике.

 Закон распределения времени обслуживания B(t) также экспоненциальный, причем процессы обслуживания в каждой очереди независимы. Это предположение не может быть выполнено, поскольку время обслуживания пакета пропорционально его длине, и, следовательно, нельзя говорить о независимости времен обслуживания в очередях.

Однако моделирование показывает [9], что применение формулы (4) дает приемлемую оценку средней задержки пакета в сети.

Имитационное моделирование позволяет имитировать поведение реальной ЛВС. Имеется много программных средств для имитационного моделирования компьютерных сетей (GPSS, COMNET III фирмы Caci Products Co., BONeS Designer фирмы Cadence Inc., OPNET фирмы Modeler Mil3 Inc., ns2 и др.).

Литература

1. Анкудинов Г.И., Стрижаченко А.И. Сети ЭВМ и телекоммуникации (архитектура и протоколы): Учеб.пособие. – 2-е изд. СПб.: СЗТУ, 2003. 72с.

2. Олифер В.Г., Олифер Н.А. Компьютерные сети. Принципы, технологии, протоколы. – СПб.: Питер, 2002. – 672 с.

3. Компьютерные сети: Учебный курс / Пер. с англ.– М.: ТОО «Channel Trading Ltd», 1997.– 696 с.

4. Советов Б.Я., Яковлев С.А. Построение сетей интегрального обслуживания. – Л.: Машиностроение, 1990. – 332 с.

5. Англо-русский словарь по сетям и сетевым технологиям / Сост. С.Б.Орлов. – М.: «Солон», 1997. – 301 с.

6. Кульгин М. Технологии корпоративных сетей: Энциклопедия. – СПб.: Изд-во «Питер», 2000. – 704 с.

7. Гук М. Аппаратные средства локальных сетей: Энциклопедия.– СПб.: Изд-во «Питер», 2000. – 576 с.

8. Ногл М. TCP/IP: Учебник.- М.: ДМК Пресс, 2001. 480 с.

9. Новиков Ю.В., Кондратенко С.В. Локальные сети: архитектура, алгоритмы, проектирование. М.: Изд-во ЭКОМ, 2000. 312 с.

10. Уолрэнд Дж. Телекоммуникационные и компьютерные сети: Вводный курс/ Пер. с англ.- М.: Постмаркет, 2001. 480 с.

11. Томашевский В., Жданова Е. Имитационное моделирование в среде GPSS.- М.: Бестселлер, 2003.- 416 с.

12. Советов Б.Я., Яковлев С.А. Моделирование систем: Учеб. пособие. - М.: Высш. шк., 1985.- 271 с.

13. Петухов О.А. Модели систем массового обслуживанияю: Учеб. пособие.- Л.: СЗПИ, 1989.- 86 с.

Примеры использования имитационного

моделирования

Обеспечение точности и достоверности

результатов моделирования

Число испытаний N определяет точность результатов моделирования. Пусть необходимо определить точность оценки параметраx случайной величины x. Вероятность

P(a –x < ) = ,

где a – точное значение параметра, называется достоверностью оценки, а величина  – абсолютной точностью оценки.

Величина ₀ =  / a называется относительной точностью оценки. Тогда достоверность оценки

P(a –x  / a < ₀ ) = .

Число реализаций для оценки среднего значения случайной величины

Для оценки среднего значения используем формулу

.

В соответствии с центральной предельной теоремой при больших N величинаx распределена по нормальному закону с математическим ожиданием a и дисперсией ²/( N – 1). Тогда

и требуемое число реализаций

.

Величина t_ берется для заданной достоверности  из таблицы нормального распределения.

	0.8	0.85	0.9	0.95	0.997
t	1.28	1.44	1.64	1.96	3

Поскольку дисперсия оцениваемой величины неизвестна, необходимо провести 50-100 предварительных испытаний и оценить величину .

Для дисперсии ² точность оценки , где ₄ – центральный момент четвертого порядка случайной величины x. Для нормального распределения ₄ =3⁴.

Пример 1.

Дано:

• структурная схема вычислительной системы (обеспечивающая часть локальной информационной технологии);

• пакетный режим работы вычислительной системы;

• интенсивность входного потока заданий  = 0.2 [1/с] (экспон. распределение);

• время решения задания в вычислительной системе не должно превышать

T _доп = 30 с для 90 % заданий;

• математическая модель вычислительной системы в виде однопотоковой однолинейной системы массового обслуживания типа M/M/1/ (рис. 1).

Н айти:

• значение параметра – среднюю интенсивность обслуживания заявок в приборе , при которой время пребывания любой заявки в СМО t не будет превышать заданной величины (30 с) для 90 % заявок:

Р{ t 30} = 0.9

(1)

• по найденному  вычислить системные характеристики СМО;

• по найденному  определить подходящий тип вычислительной системы и ее показатели производительности, обеспечивающие требуемое время решения задачи.

Ограничения:

• загрузка вычислительной системы  = / (обслуживающего прибора в математической модели) не должна превышать 0.7.

Решение:

Уравнение (1) определяет значение функции распределения вероятностей (ФРВ) случайной величины t в точке 28.5, равное 0.9. Для системы M/M/1/ (и только для нее) известно аналитическое выражение ФРВ t. Тогда для отыскания неизвестных  и  можно составить систему нелинейных уравнений:

(2)

Решение нелинейной системы уравнений (2):

-( – )30 = ln 0.1,

 = - ln 0.1/30+0.2 = 0.276753,

 = / = 0.2 / 0.276753 = 0.722.

Выберем  = /0.7 = 0.2/0.7 = 0.285714.

Тогда расчетные значения среднего времени задержки пакета в СМО:

T = 1/ ( – ) = 11.67 с.

Среднее число транзактов в СМО:

L =  / ( – ) = 2.334.

Среднее число транзактов в очереди:

L_W = L –  = 2.334 – 0.722 = 1.612.

Для выбора подходящей вычислительной системы (сервера) зададим параметры пакета программ для обработки. Пусть любой пакет содержит 100 программ по 10000 операторов каждая. Тогда общий объем пакета в операторах составит Q=10⁶ операций. При этом требуемая производительность вычислительной системы (сервера) будет равна V=Q=10⁶0.285714 300 тыс. оп./с. Для определения подходящей вычислительной системы (сервера) воспользуемся данными таблицы 1.

Таблица 1. Производительность процессоров фирмы INTEL

Тип процессора	Тактовая частота, МГц	Производительность, млн. оп./с
8086	8	0.66
286	12	2.66
Intel 386 DX	33	11
Intel 486 DX	33	27
Intel 486 DX2	66	54
Pentium	66	112

Из перечня процессоров заданным требованиям удовлетворяет младшая модель процессора - 8086.

Полученные по математическим моделям результаты не всегда адекватно отражают реальную работу вычислительной системы заданной структуры, так как расчетные аналитические формулы выведены и верны лишь при упрощающих допущениях (или предположениях) относительно структуры, распределениях потоков и обслуживания и других. Альтернативным подходом к решению поставленной задачи является непосредственная имитация на ПЭВМ (имитационное моделирование) процесса выполнения пакета в вычислительной системе заданной структуры с использованием системы моделирования GPSS.

Программа моделирования на языке GPSS/H (студенческая версия).

SIMULATE

EXPON FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915/

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3/

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9/

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

TABLA TABLE M1,0,3500000,15

GENERATE 5000000,FN$EXPON 1/ =1/ 0.2= 5.0

* 1 единица модедьного времени = 1 мкс

QUEUE 1

SEIZE PRIB1

DEPART 1

ADVANCE 3500000,FN$EXPON 1/ =3.5 с

RELEASE PRIB1

TABULATE TABLA

TERMINATE 1

START 15000

END

Результаты моделирования (см. листинг 1) сведены в табл.2.

Таблица 2

facility (устройство)	Параметр	Значение	Интерпретация
PRIB1	TOTAL TIME (коэффициент загрузки)	0.692	 = 0.692
	AVERAGE TIME/XACT (среднее время обслуживания на транзакт)	3498076.195	TS = 1/ = 3.498076 с
QUEUE 1 (очередь)	AVERAGE CONTENTS (средняя длина)	1.634	LW = 1.634
	MAXIMUM CONTENTS (макс. длина)	29	LW макс=29
	AVERAGE TIME/UNIT (среднее время ожидания)	8261343.624	W =8.261344 с
TABLE TABLA (табличные данные для полного времени в СМО)	MEAN ARGUMENT (среднее время в СМО на 1 транзакт)	1.1759E+07	T = 11.759 с
	STANDARD DEVIATION (среднеквадратическое отклонение времени в СМО на 1 транзакт)	1.2982E+07	=1.2982 с

Результаты моделирования хорошо совпадают с расчетными значениями.

Пример 2.

Рассмотрим решение задачи для диалогового режима работы локальной вычислительной системы.

Дано:

• режим работы - диалоговый;

• время реакции диалогового абонента (время обдумывания) 1/=10с;

• время решения задания (время ответа на запрос с терминала) не должно превышать T_{d доп} =1 с для 90 % заданий;

• число пользователей n=20;

• математическая модель вычислительной системы в виде замкнутой сети массового обслуживания (рис. 2).

Р ис. 2

В этой модели постоянно циркулируют n заявок (транзактов).

Найти:

• значение параметров сети массового обслуживания  , при которых

t  T_{d доп} 1 c для 90 % диалоговых заявок, т.е.

P{ t1 c } = 0.9;

• по найденным  и  вычислить системные и сетевые характеристики СеМО;

• определить подходящий тип вычислительной системы и ее показатели производительности, обеспечивающие требуемое время ответа на запрос с терминала.

Ограничения:

• загрузка вычислительной системы (сервера) не должна превышать 0.8.

Решение:

Для решения задачи используется приближенный метод, основанный на декомпозиции вычислительной системы на подсистему обработки и терминальную подсистему (и их “независимом” рассмотрении) с последующим балансом потоков в этих подсистемах. Тогда для отыскания неизвестных  можно составить систему уравнений:

1 – e - ( – )Td доп =P	(3)
   	(4)
	(5)

Из первого уравнения

 -  = - ln(1-P) / Td доп.

(6)

Подставим  -  в последнее уравнение

(7)

Для P = 0.9, T_{d доп} = 1 с, 1/=10с, n=20 получаем:

 = 20 / (10 – 1 / ln (1–0.9)) = 2.09080,

 =  - ln(1–P) / T_{d доп} = 2.09080 – ln (1–0.9) / 1 = 4.39339,

 =  /  = 0.475897 – коэффициент загрузки.

Расчет можно несколько упростить, если учесть, что T_{d доп}  T_d /2 (для P = 0.9), где T_d =1/( – ) - среднее время ответа. Тогда T_d  2T_{d доп} и

.  20/(10-2*1) = 2.5.

Программа моделирования на языке GPSS/H (студенческая версия).

SIMULATE

INITIAL X6,5000

SPACE STORAGE 20

EXPON FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915/

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3/

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9/

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

QTIME QTABLE QU1,0,200,20

GENERATE 0,0,,1

SPLIT 19,SYS0,1

SYS0 ENTER SPACE

ADVANCE 10000000,FN$EXPON

LEAVE SPACE

QUEUE QU1

SEIZE PRIB1

DEPART QU1

ADVANCE 250000,FN$EXPON

RELEASE PRIB1

SAVEVALUE 6-,1

TEST E X6,0,SYS0

TERMINATE 1

START 1

END

Результаты моделирования для 4 значений  сведены в табл.3 (см. листинг 2 для  = 4 [1/с]).

Таблица 3

 [1/с]	Результаты моделирования					TS + Tw [с]
		TS [с]	LW	LW МАКС	Tw [с]
2	0.844	0.505	2.343	15	1.402	1.907
3	0.622	0.337	0.801	9	0.718	1.055
4	0.481	0.253	0.381	7	0.200	0.453
5	0.390	0.202	0.220	6	0.114	0.316

В этой таблице

T_S – среднее время обработки запроса;

L_W – среднее длина очереди;

L_{W МАКС} – максимальная длина очереди;

T_w – среднее время ожидания запроса в очереди;

T_S + T_w – среднее время ответа.

Для выбора подходящей вычислительной системы (сервера) следует выбрать вариант с

 = 4 или 5 [1/с].

Пример 3.

Рассмотрим решение задачи для смешанного режима работы локальной вычислительной системы, когда для одной группы абонентов модель вычислительной системы представляется замкнутой диалоговой СеМО (сети СМО), а для другой группы - разомкнутой СеМО.

Дано:

• режим работы - смешанный;

• время реакции диалогового абонента (время обдумывания) 1/=10с;

• время решения задания диалогового абонента (время ответа на запрос с терминала) не должно превышать T_{d доп} =1 с для 90 % заданий;

• число пользователей n=20;

• время ответа T_{p доп} для 90 % пакетных заданий не более 20 с;

• интенсивность потока пакетных заданий  = 0.01 [1/с].

• м атематическая модель вычислительной системы в виде смешанной сети массового обслуживания (рис. 3).

Рис. 3

Найти: