
- •ФИЗИКА
- •Объем учебной работы по текущему семестру:
- •ЛИТЕРАТУРА
- •Тема 1. Тепловое излучение
- •Количественные характеристики теплового
- •Величина
- •Закон Кирхгофа
- •1.2. Законы теплового излучения абсолютно
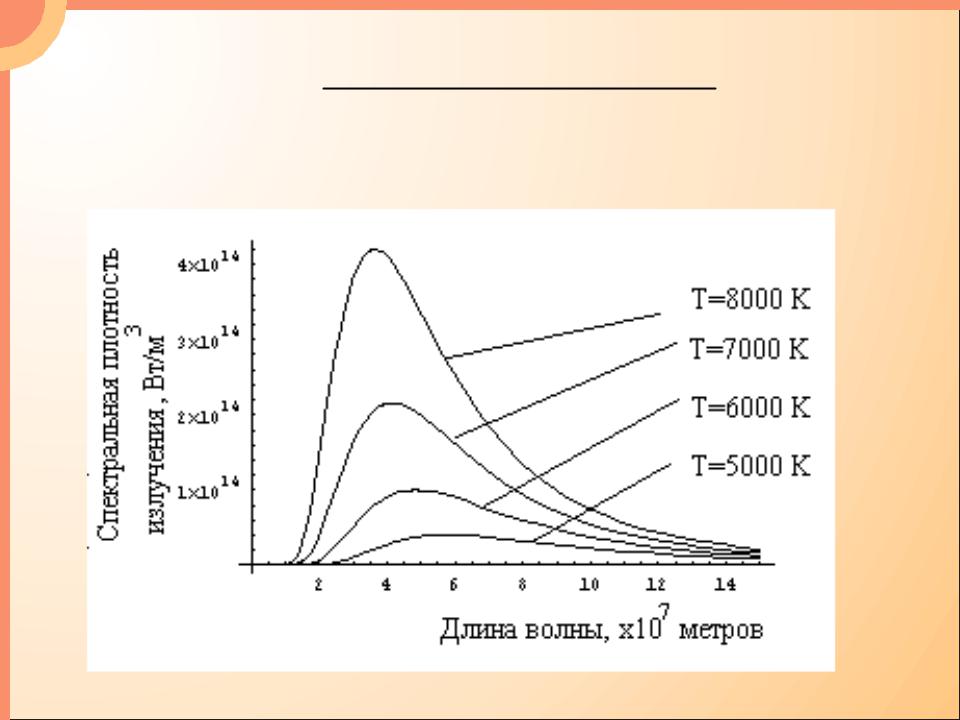
- •Закон смещения Вина
- •Второй закон Вина
- •Дано:
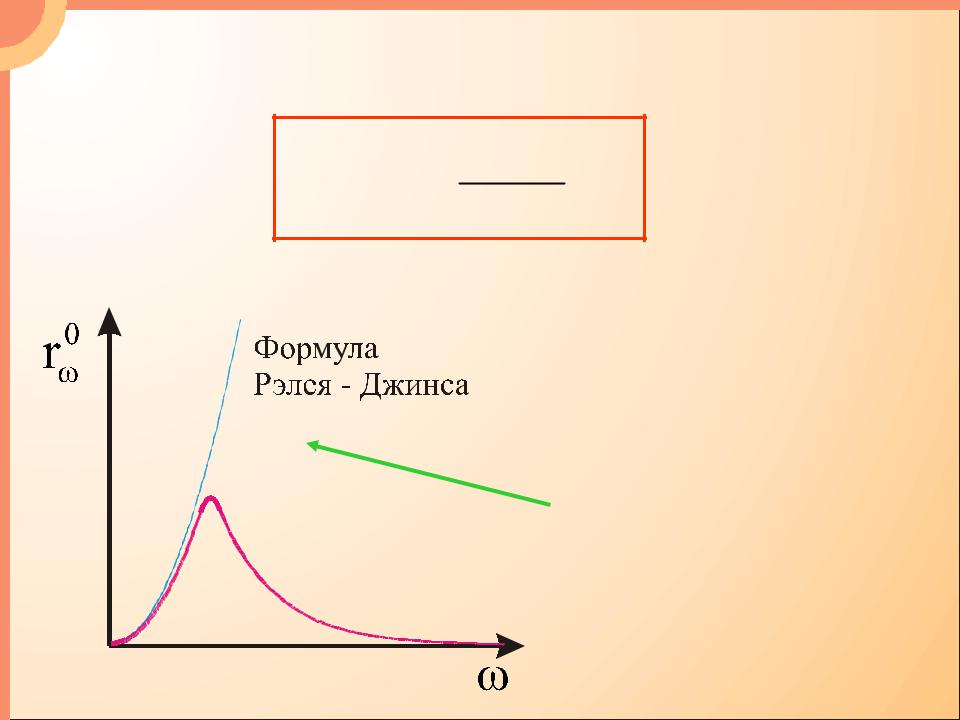
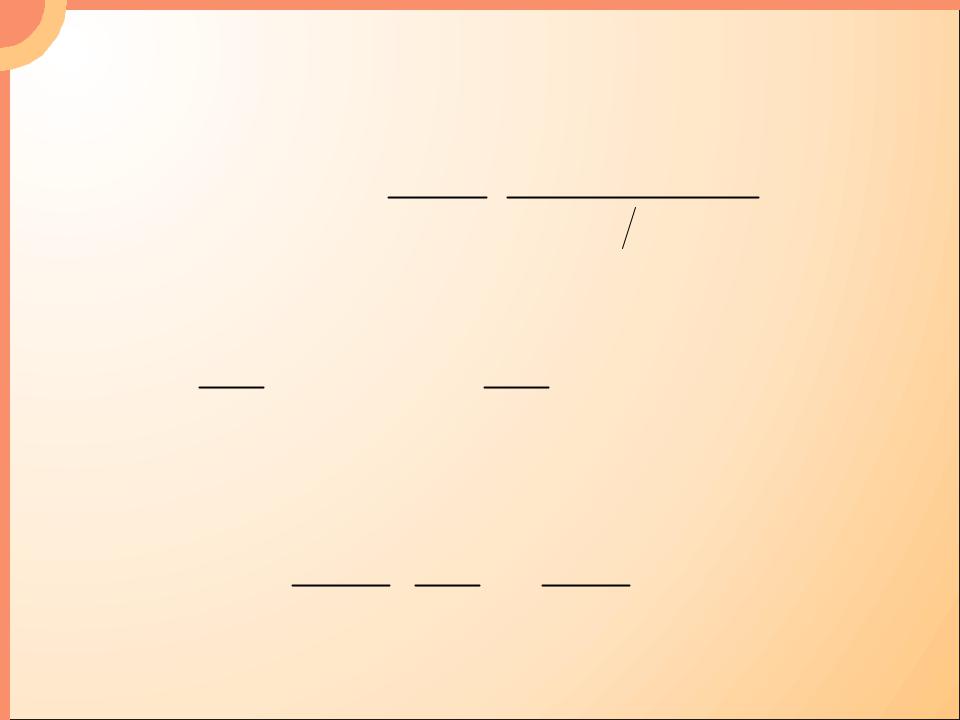
- •Формула Рэлея-Джинса:
- •Объемная плотность энергии, приходящаяся на
- •Формула Рэлея-Джинса:
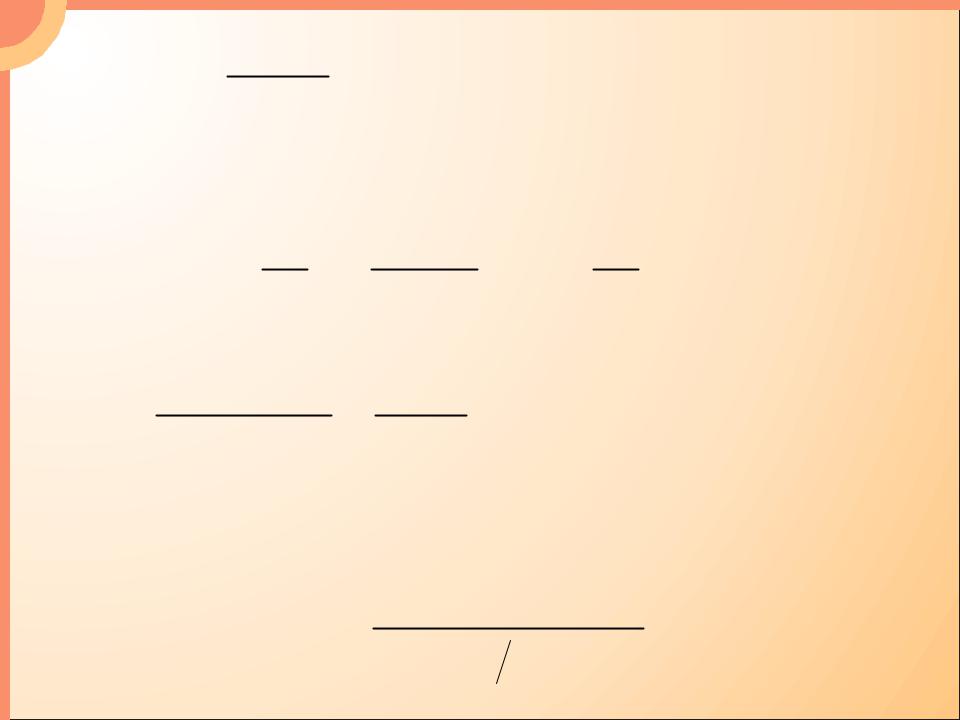
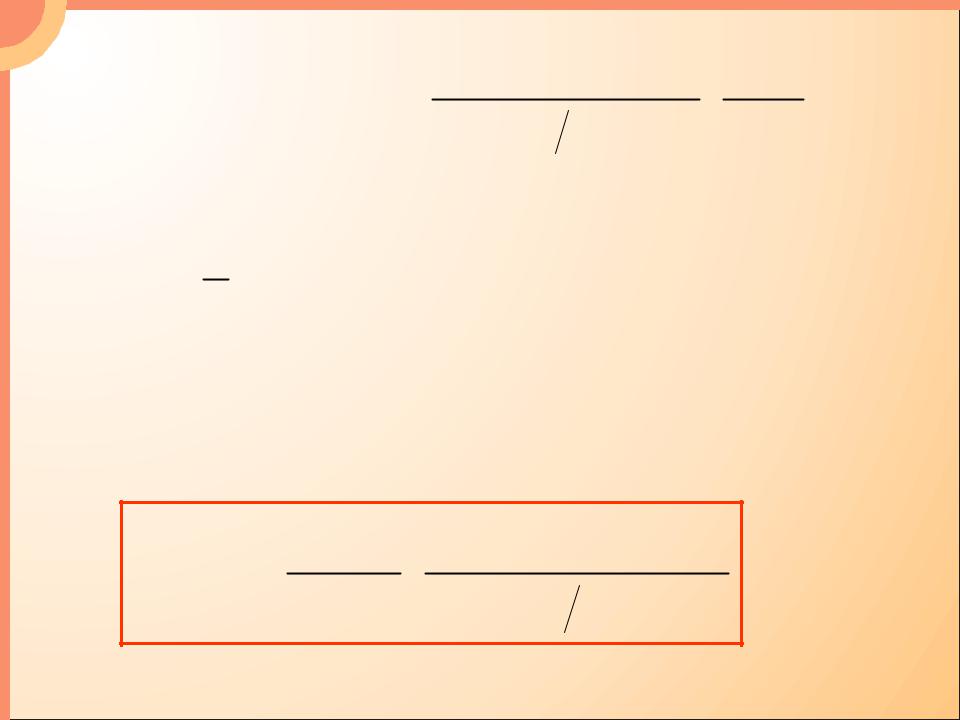
- •1.3. Формула Планка
- •Равновесное излучение подчиняется закону распре-
- •В области длинных волн формула Планка переходит
- •Из формулы Планка следует и закон Стефана –
Формула Рэлея-Джинса: |
|
||
0 |
2 |
(1.12) |
|
r ,T |
4 2c2 kБT |
||
|
|||
|
«Ультрафиолетовая |
||
|
|
катастрофа» |
|

1.3. Формула Планка |
|
|
|
|
1900 г. |
|
|
|
|
h h |
h |
|
|
(1.13) |
2 |
2 |
|
|
|
h 6,62 10 34 |
Дж с |
|
||
1,054 10 34 |
Дж с |
|
||
n n |
|
|
(1.14) |
|
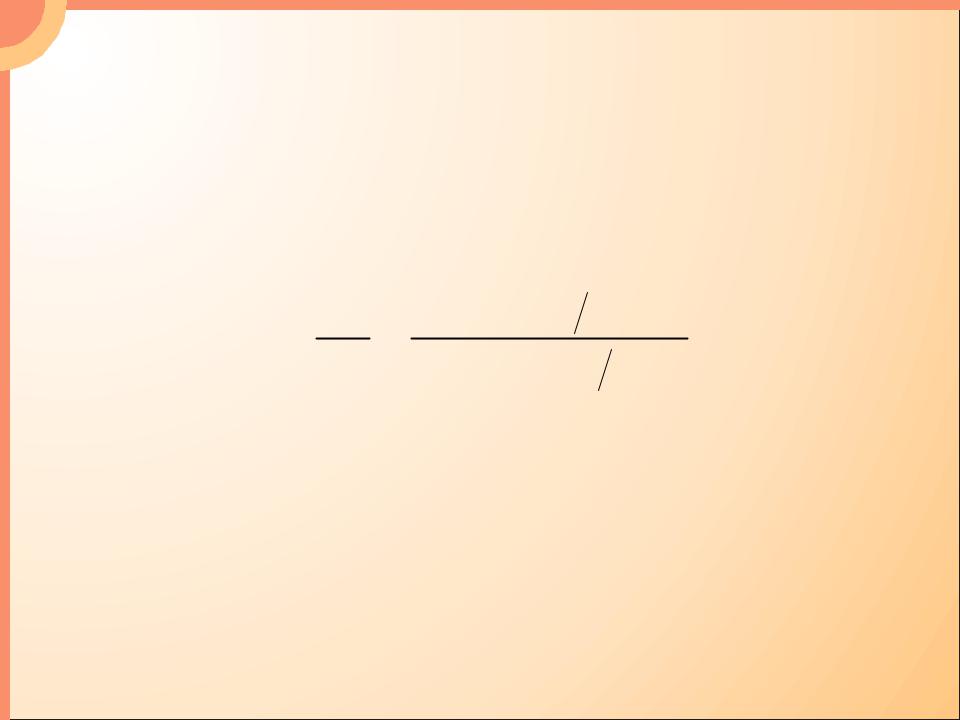
Равновесное излучение подчиняется закону распре- |
|||
деления по энергии Больцмана, следовательно, |
|||
вероятность того, что энергия колебания с частотой ω |
|||
имеет значение εn, равна: |
|
||
P Nn |
exp n kБT |
(1.15) |
|
n |
N |
exp n kБT |
|
|
|
||
|
|
n |
|
Среднее значение энергии колебания: |
|
||
|
|
Pn n |
(1.16) |

1.14 |
и 1.15 |
|
1.16 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
n exp n kБT |
|
|
||||||
|
n 0 |
|
|
|
|
|
|
|
(1.17) |
|
|
|
|
exp n kБT |
|
|
|
||||
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x k T |
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n e nx |
|
d |
|
|
nx |
(1.18) |
||
|
n 0 |
|
|
|
|
|||||
|
|
|
dx |
ln e |
|
|||||
|
|
e |
nx |
|
|
n 0 |
|
|
||
|
|
|
|
|
|
|
||||
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
e nx |
|
x |
|
|
|
|
|
|
|
|
|
|
||
n 0 |
1 e |
|
|
|
|
|
|
|
|
|
|
|
||
|
d |
|
|
|
|
1 |
|
|
d |
ln 1 e |
x |
|
||
|
ln |
1 |
e |
x |
dx |
|
||||||||
|
|
|
dx |
|
|
|
|
|
|
|||||
|
1 e x |
|
|
|
|
|
|
|
|
|||||
|
1 e x |
|
|
|
ex 1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.19) |
|
|
exp kБT 1 |
|
|||||||||||
|
|
|
|
|||||||||||
u ,T d dn |
|
|
|
2 |
d |
|
|
|
|
exp kБT 1 |
2c3 |
|
|
r0 ,T c u ,T |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
Формула Планка: |
|
|
|
|
|
|
0 |
3 |
|
1 |
|
|
(1.20) |
r (T ) 4 2c2 |
exp( k T ) 1 |
|
||||
|
|
|||||
|
|
|
Б |
|
|
|
r0 |
4 2 c2 |
|
1 |
(1.21) |
,T |
5 |
exp( 2 c / kБT ) 1 |
|
|
|
|
|||

В области длинных волн формула Планка переходит |
|||||||
в классическую формулу Рэлея-Джинса. |
|
||||||
При |
0 |
показатель экспоненты становится |
|||||
много меньше единицы. Разлагая экспоненту в |
|||||||
степенной ряд, и учитывая только два первых члена |
|||||||
разложения, получим: |
|
|
|
|
|||
|
|
exp / kБT 1 |
, |
|
|
||
|
|
|
|
|
k T |
|
|
|
|
|
|
|
Б |
|
|
r0(T ) |
3 |
|
1 |
|
2 |
k T |
|
|
|
|
|||||
|
|
4 2c2 |
1 |
1 |
4 2c2 |
Б |
|
|
|
|
|||||
|
|
|
|
k T |
|
|
|
|
|
|
|
Б |
|
|
|
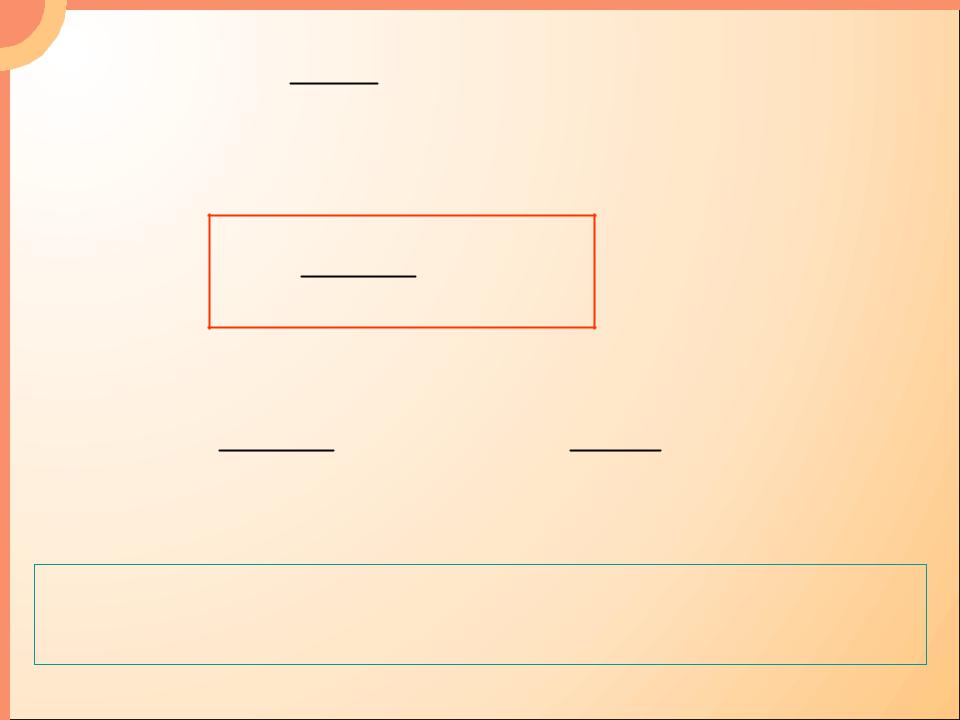
Из формулы Планка следует и закон Стефана – |
|||||||||||||
Больцмана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
d |
|
||
|
|
|
|
|
|
|
|
|
|||||
RЭ0 r0 T d |
2 |
c |
2 |
|
|
|
|||||||
0 |
|
|
|
0 |
4 |
|
|
exp kБT 1 |
|
||||
x |
|
|
|
|
|
|
k T |
dx |
|
||||
|
|
d |
|
|
Б |
|
|
||||||
|
kБT |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
k T |
|
4 x3dx |
(1.22) |
|||||
|
RЭ |
4 2c2 |
|
Б |
|
|
0 ex 1 |
||||||
|
|
|
|
|
|
|
|
||||||
|
|
x3dx |
4 |
|
|
|||
|
|
0 ex 1 15 |
|
|
||||
RЭ0 |
|
|
2kБ4 |
T 4 T 4 |
|
(1.23) |
||
|
|
|
60c2 3 |
|
|
|
||
|
2k 4 |
|
5,6696 10-8 |
Вт |
|
|||
|
Б |
|
|
|
||||
|
60c2 3 |
|
м2К4 |
|
||||
Полученная Планком формула дает исчерпывающее |
||||||||
описание равновесного теплового излучения. |
|
|||||||
