4.5. Погрешность измерений

Погрешностью называется отклонение результата измерения от истинного значения измеряемой величины. Погрешность воз­никает вследствие несовершенства метода измерения — методи­ческая, неисправности или неправильной установки измерительного прибора — инструментальная, недостаточного внимания иле умения оператора — субъективная. Измерения выполняются в не­которых условиях, которые определяются величинами, не изме­ряемыми прибором, но влияющими на его показания. К таким влияющим величинам относятся: температура, влажность и дав­ление окружающего воздуха; колебаиия напряжения или часто­ты электрической сети, питающей измерительный прибор; нали­чие сильного внешнего электромагнитного, поля. Погрешность на­зывается основной, если влияющие величины находятся в преде­лах значений, при которых прибор градуировался, и дополнитель­ной, если одна из влияющих, величин отклоняется от нормально­го значения или выходит за пределы нормальной области значе­ний. Любая погрешность состоит из двух составляющих — систе­матической и случайной.

Систематическая погрешность в процессе повторных измере­ний остается постоянной или изменяется по некоторому закону. В обоих случаях она легко обнаруживается и может быть исклю­чена из результата измерения.

Случайная погрешность при повторных измерениях одной и той же величины одним и тем же прибором изменяется случай­ным образом. Иногда случается грубая погрешность, возникаю­щая вследствие ошибки оператора, сильной внешней помехи и т. д. Значение с грубой погрешностью учитывать не следует.

Точностью измерения называют качество измерения, отражаю­щее близость полученного результата к истинному значению. Ис­тинное значение неизвестно, поэтому вместо него принимают дей­ствительное значение, которое равно среднему арифметическому, полученному в результате нескольких измерений, выполненных в неизменных условиях. Например, при десяти измерениях напря­жения получили следующие показания вольтметра:

Номер измерения 1 2 3 4 5 6 7 8 9 10

Показание, В 105 103 97 99 101,5 98 102 104 100 100,5

Среднее арифметическое находится по формуле

(1)

где i= 1, 2, 3, ... — номер единичного измерения, a_i — показание,. n — число измерений.

Подставляя в (1) данные из нашего примера, находим дей­ствительное -значение .напряжения U=101 В.

Для количественной оценки погрешностей (введены понятия аб­солютной, относительной и приведенной погрешностей.

Абсолют­ная погрешность Δ равна разности между измеренным А_изм к действительным А значениями измеряемой величины и выража­ется в единицах последней:

(2)

Относительная погрешность равна отношению абсолютной зпо-тоещн'ости к измеренному значению или действительному:

(3)

Относительная погрешность при неизменной абсолютной возрас­тает к началу шкалы, поэтому для повышения точности измере­ния -нужно выбирать прибор с такими пределами, чтобы указа­тель при отсчете находился вблизи конечного значения шкалы. Для обеспечения этого требования многие приборы выпускаются с несколькими шкалами (многопредельные приборы).

Для сравнения приборов между собой введено понятие приве­денная погрешность, которая равна отношению абсолютной пог­решности к конечному значению шкалы:

(4)

Если прибор снабжен двусторонней шкалой с нулевой отметкой посередине, то за А_к принимается арифметическая сумма обоих конечных значений.

Абсолютная и относительная погрешности многих приборов зависят от значения измеряемой величины. Для таких приборов пределы допустимой погрешности представляются в виде двух слагаемых — зависимого и независимого от измеряемой величины.

Абсолютная допустимая погрешность , гдеа — постоянная погрешность в единицах измеряемой величины, b — постоянное дробное число. Например, погрешность установки ча­стоты генератора ГЗ-33 , Гц.

Относительная погрешность %, или, %, гдес и d в процентах. Например, погреш­ность измерения постоянного напряжения вольтметром ВК7-10А/1 , %

Для измерительных приборов с дискретным счетом (цифро­вых) допускается и такое выражение предельной допустимой аб­солютной погрешности: А=(b, % от А_изм+т ед. счета), где т — погрешность дискретности, выбирается из ряда чисел 0,5; 1; 2.

Предел допускаемой погрешности можно выражать и в деци­белах: , гдеК=10 при измерении напряжения или тока, К = 20 при измерении мощности.

Следует отметить, что в силу особенностей радиотехнических измерений и различных требований к точности измерений погреш­ность радиоизмерительных приборов и измерений колеблется в значительных пределах. Например, относительная погрешность измерения частоты при использовании резонансных частотомеров «оставляет 0,05—0,5%, а при использовании цифровых — 1∙10^-7 и даже 10^-9. Погрешность измерения напряжения стрелочным вольтметром колеблется от 1,5 до 6%, а цифровыми — 0,05—1,0%. Погрешность измерения потока мощности прибором ПЗ-9 превы­шает 30%.

Рассмотрим способы уменьшения погрешностей и оценку ре­зультатов измерений. Систематические погрешности уменьшаются (исключаются) следующими способами: установкой указателя в нулевое положение перед началом измерения и проверкой этого положения в процессе измерения; использованием поправок или поправочных множителей, полученных при поверке данного при­бора; проверкой некоторых точек шкалы прибора по образцовым сигналам; калибровкой показаний по внутренним сигналам, пре­дусматриваемым в сложных приборах; размещением прибора в экранированном помещении. Используя подобные способы, будем считать, что систематические погрешности устранены и на резуль­тат измерения влияют только случайные.

Случайные погрешности уменьшают путем выполнения ряда единичных измерений измеряемой величины в одних н тех же условиях. Действительное значение вычисляют по (1). Чем больше число единичных измерений п, тем ближе действительное значение к истинному. Однако практически п выбирают в пре­делах 10—20.

Располагая действительным значением А и показанием при единичном измерении щ, можно вычислить абсолютную погреш­ность каждого из них: Воспользуемся примером на стр. 10 и определим Δ_i:

Номер измерения 1 2 3 4 5 6 7 8 9 10

Абсолютная пог­решность Δ, В 4 2 -4 -2 0,5 -3 1 3 -1 -0,5

Заметим, что при правильном выполнении вычислений сумма аб­солютных погрешностей всех единичных измерений равна нулю:

Для оценки случайной погрешности единичного измерения вве­дено понятие среднеквадратического отклонения (погрешности) а,. которое вычисляется по следующей формуле:

а для оценки случайной погрешности результата измерения, т. е. действительного значения, аналогично:

Оценим случайные 'погрешности рассмотренного выше примера-. Подставляя абсолютные погрешности каждого измерения в (В.5), найдем cреднеквадратическую погрешность единичного измерения σ=2,6 В. Среднеквадратическэя погрешность результата измере­ния, согласно (В.6), σрез=0,83 В. Результат измерения напряжения следует записать так: U = 101 ± 1 В.

1 Максимальная допустимая погрешность единичного измерения принимается равной 3 σ (иногда 2 σ); если погрешность превышает это значение, то считается грубой погрешностью и такое показа­ние отбрасывается.

Погрешности нужно суммировать в том случае, если общая по­грешность определяется частными: например, погрешность изме­рительного прибора, в состав которого входят измерительные пре­образователи, (встроенные измерители других величин и т. д., оп­ределяется погрешностями этих узлов.

Систематические погрешности суммируются алгебраически. Случайные, если они независимы друг от друга, — геометричес­ки, а если зависимы — алге­браически.

Погрешности косвенных из­мерений определяются через погрешности прямых измерений. Способ вычисления ре­зультирующей погрешности за­висит от вида функциональной связи искомой величины с ее личинами, подвергаемыми пря­мым измерениям. Общие правила вычислений выводятся методом дифференциального исчисления. Мы рассмотрим несколько примеров типичных функ­циональных зависимостей.

1. Искомая величина зависит от суммы измеряемых прямым методом величин. Напряжение на двух резисторах (рис. В.1а) из­меряется одним вольтметром. Напряжение на первом резисторе оказалось равным Ui с погрешностью ΔU_t и на втором — U₂ с погрешностью ΔU₂. Общее напряжение U=Ui + U₂. Погрешности косвенного измерения: абсолютная ; относи­тельная

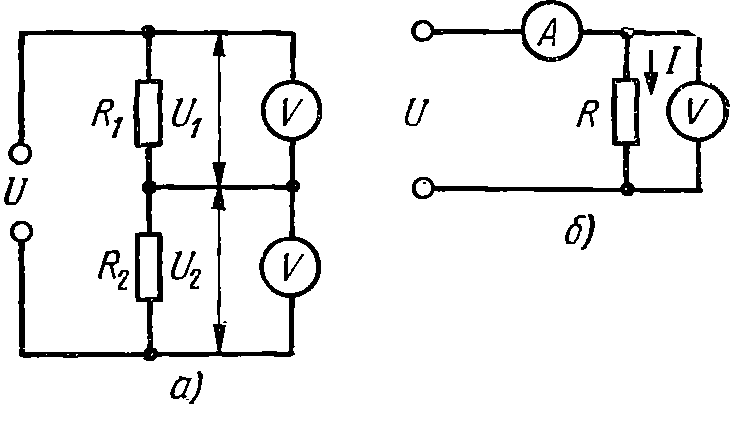
Рис. 1. К определению погрешностей косвенных измерений

2. Искомая величина зависит от произведения двух величин. Например, нужно определить мощность постоянного тока Р= UI, потребляемую резистором R (рис. В. 16), по прямым изме­рениям тока и напряжения. Погрешности прямых измерений ΔU и ΔI.

Погрешности косвенного измерения:

абсолютная

относительная

3. Определяемая величина зависит от частного двух других паяример, сопротивление постоянному току резистора по изме' Ценным значениям тока и напряжения с погрешностями прямых измерении ΔU и ΔI. Сопротивление резистора R = U/I абсолютная погрешность относительная