Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт им Г.В. Плеханова

(технический университет)

Кафедра информатики и компьютерных технологий

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ

Курс лекций

Составитель: доц. Беляев В.В.

САНКТ-ПЕТЕРБУРГ

2000

Назначение и типы моделей

Общие понятия.

Система – совокупность элементов , находящихся во взаимодействии и образующих единое целостное образование со свойствами, отличными от свойств отдельных элементов.

Структура системы – это описание её организации, определяющее возможность разделения на отдельные элементы и их отношения.

Состояние системы определяется значением ряда характеризующих параметров.

Чем сложнее система тем больше параметров необходимо определить для описания ее состояния.

Операция – целенаправленное изменение состояния системы.

Проведение операции предполагает изменение одних характеристик системы –так называемых параметров x1, x2,…xn при учете других - условий операций a1,a2,…am.

Во главе операции стоит руководитель (лицо принимающее решение –ЛПР), который принимает решение относительно ее параметров, обеспечивающих достижение цели при существующих условиях.

Цель операции – предвосхищаемый результат на который направлено действие. В цели должны содержаться значения параметров системы, соответствующие моменту ее достижения.

Критерий эффективности операции К , который позволяет свести задачу выбора варианта к следующей схеме - из двух вариантов операции (x₁⁽¹⁾ , x₂⁽¹⁾ ,…x_n⁽¹⁾ ) и (x₁⁽²⁾ , x₂⁽²⁾ ,…x_n⁽²⁾) выбирается тот для которого значение эффективности больше(меньше).

Достижение цели должно обеспечивать максимум (минимум) критерия эффективности при выполнении наложенных ограничений.

Таким образом цель операции имеет вид

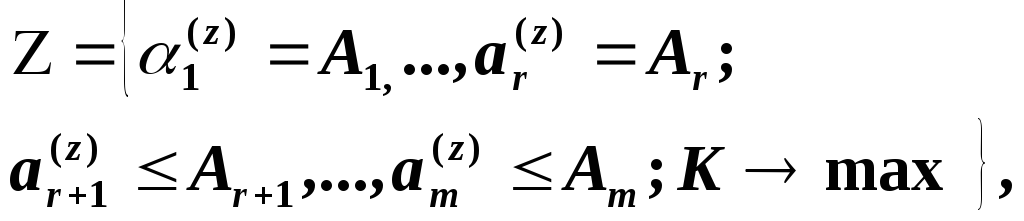
где - контролируемые параметры системы на момент достижения цели;- условия проведения операции; K- критерий эффективности операции.

Модель – специально созданная материальная или формальнологическая система, находящаяся в объективном соответствии с исследуемым объектом, моделированием отражающая наиболее существенные его свойства и дающая в процессе изучения информацию о нем. Процесс построения и изучения модели называется моделированием.

Практическое значение модель приобретает если её изучение имеющимися средствами более доступно, чем изучение самого объекта.

В зависимости от выбора средств моделирования различают материальные и идеальные модели.(Рис.1.1).

При материальном моделировании создают подобие изучаемого объекта из подобных материалов или подбирают аналогично протекающий процесс другой физической природы.

При решении операционных задач используют знаковые модели, к которым относятся словесные описания, графические и математические модели.

Математическая модель – система математических выражений, описывающих взаимосвязь характеристик объекта моделирования, анализ которых позволяет получить дополнительную информацию о системе, принять инженерное решение.

Вид модели, математический аппарат их построения и исследования определяются свойствами моделируемой системы и в первую очередь типом ее элементов.

При моделировании производственных процессов выделяют два типа параметров: детерминированные и стохастические.

Детерминированные –имеют количественную меру и сохраняют свое значение при неизменных определяющих условиях. Эти параметры могут быть получены путем изменений и расчетов с любой доступной точностью.

Стохастические параметры – случайные величины, изменяющиеся в процессе работы.

Важно понять следующее: математическая модель системы – это не просто формальная запись некоторой абстрактной функции, существующей на множестве действительных чисел, а описание взаимосвязи параметров реального объекта, лежащих в определенных условиях. Т.е. модель всегда предполагает выполнение следующего гипотетического условия – если X и Y – параметры системы и она находится в допустимом состоянии, то реальные значения параметров X и Y будут связаны соотношением, описанным моделью. В случае детерминированных параметров предполагается, что каждому состоянию системы соответствует единственное значение детерминированного параметра, которое сохраняется, если состояние системы остается неизменным. Стохастические параметры могут менять свое значение при неизменном уровне других показателей.

Лежащий в основе моделирования принцип воспроизводимости результатов предполагает, что состояние системы может быть повторено любое число раз и соответственно определены значения ее параметров. Именно воспроизводимость результатов позволяет планировать развитие производства в будущем, но этот принцип заставляет строго разделить стохастические и детерминированные параметры.

Тип параметров системы определяет возможные взаимосвязи между ними, а следовательно и модель, описывающую эту взаимосвязь.

Между детерминированными параметрами, с учетом их физической сущности и единиц измерения, возможны следующие взаимосвязи:

равенство x=y;

неравенство x<y;

функциональная связь в виде числовой функции действительных переменных y = F ().

В этом случае модели будут иметь вид систем уравнений и неравенств, составленных на основе теоретических расчетных формул, физических законов, аналитических зависимостей, полученных в процессе анализа системы. Конкретные числовые значения коэффициентов функций получаются путем измерений или расчетов. При получении, исследовании и преобразовании этих моделей используются элементарная алгебра, геометрия, тригонометрия, дифференциальное и интегральное исчисления.