4.2. Критерий Фишера

F - критерий Фишераиспользуют для сравнения дисперсий двух генеральных совокупностей, распределенных по нормальному закону.

По независимым выборкам объема из этих совокупностей найдены выборочные дисперсии и. Выдвигается гипотезаH₀ - дисперсии равны, альтернативная гипотезаH₁- дисперсии не равны. Вычисляетсяпо формуле:

,

(4.5)

где - большая дисперсия,- меньшая дисперсия. По заданному уровню значимости α и числам степеней свободыи(число степеней свободы числителя ичисло степеней свободы знаменателя) - определяемпо таблицам или используя встроенные функцииMSExcel.

Число степеней свободы числителя определяется по формуле:

,

(4.6)

где n₁- число вариант для большей дисперсии.

Число степеней свободы знаменателя определяется по формуле:

,

(4.7)

где n₂ - число вариант для меньшей дисперсии.

Если (вычисленное значение критерия не больше критического), то принимается гипотезаH₀(дисперсии равны), в противном случае () принимается гипотезаH₁ (дисперсии различны).

Пример 4.3

При проведении тестирования двух одинаковых приборов были проведены измерения эталона. При этом первым прибором было проведено n₁=11 измерений, а вторым - n₂=9.

Результаты были записаны в виде отклонений от значения эталона. Требуется выяснить: одинаковой ли точностью обладают приборы.

Решение:

Величина отклонений от эталонного значения для первого прибора (n₁=11) внесена в столбец В,а для второго прибора (n₂=9) результаты - в столбец С (рис.4.4-4.5). Средние значения отклонений одинаковы и равны нулю. Следовательно, у приборов отсутствует систематическая ошибка.

Проверка точности приборов сводится к проверке совпадения дисперсий. Если дисперсии отклонений от эталонного значения статистически равны, то приборы обладают одинаковой точностью. Выдвигается гипотеза H₀ - дисперсии выборок равны, альтернативная гипотезаH₁- дисперсии не равны.

В результате расчета были получены соответственно следующие значения дисперсий: =7.35 и=2.188.

Значение критерия =7.35 /2.188 = 3.36.

Для уровня значимости α =0.05; числа степеней свободы числителяr₁ =11-1=10 и числа степеней свободы знаменателяr₂ = 9-1= 8 находим с помощью встроенной функции FРАСПОБР().F_крит= 3.347.

Поскольку то гипотезаH₀ отклоняется, и принимается альтернативная гипотезаH₁ (дисперсии различны). Следовательно, приборы имеют различную точность.

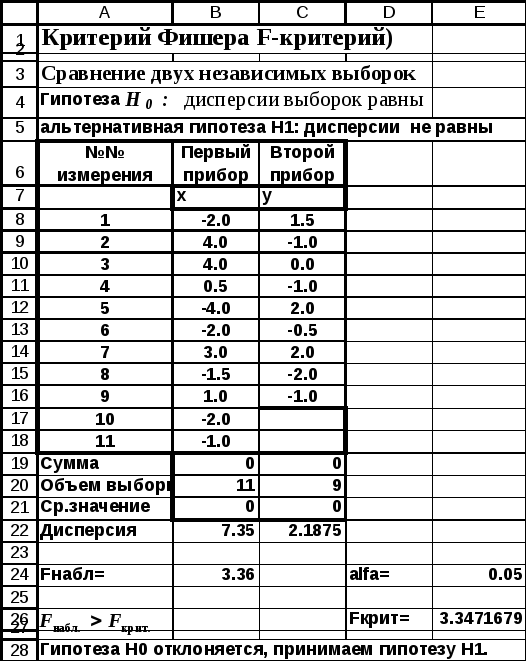
Рис. 4.4 Сравнение двух выборочных дисперсий

(фрагмент рабочего листа MSExcelв режиме отображения данных)

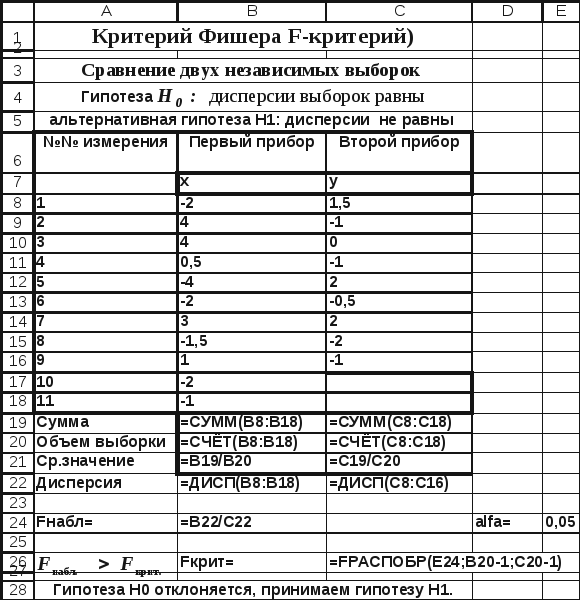
Рис. 4.5. Сравнение двух выборочных дисперсий

(фрагмент рабочего листа MSExcelв режиме отображений формул)

Средство анализа «Двухвыборочный f-тест для дисперсии» надстройки «Пакет анализа» ms Excel

Средство анализа «Двухвыборочный F-тест для дисперсии» надстройки «Пакет анализа»MSExcelслужит для проверки гипотезы о равенстве дисперсий двух выборок. Для проверки необходимо заполнить диалоговое окно, приведенное на рис.4.6, назначение всех полей ввода очевидно.

Рис. 4.6 Диалоговое окно средства анализа «Двухвыборочный F-тест для дисперсии» надстройки «Пакет анализа»MSExcel

Результаты расчета представлены на рис.4.7.

Сравните полученные результаты с результатами, полученными вручную.

Рис. 4.7 «Двухвыборочный F-тест для дисперсии»

надстройки «Пакет анализа» MSExcel