Ряд распределения случайной величины X

xi	0	1	2	3	4	5
P(xi)= pi	0,1	0,2	0,3	0,2	0,1	0,1

Поскольку появление различных значений случайной величины X – несовместные события, то вероятность того, что число опрошенных на уроке учеников равно 2 или 3, равна сумме вероятностей этих значений СВ Х (по теореме сложения вероятностей). Тогда P(Х=2 или Х=3) = P(Х=2) + P(Х=3) = 0,3 + 0,2 = 0,5.

Вероятность того, что число опрошенных на уроке учеников будет находиться в пределах от 1 до 4 (включая 1 и 4), равна 0,8, т.к.P(1≤X≤4)= P(Х=1) + P(Х=2)+ P(Х=3) + P(Х=4) = 0,8. Вероятность того ни один ученик не будет опрошенP(X= 0) = 0,1.

Задание:

1. Построить многоугольник (или полигон) распределения СВ X– числа опрошенных учеников.

2. Построить функцию распределения СВ Xчисла опрошенных учеников.

3. Используя функцию распределения, найти вероятность того, что число опрошенных на уроке учеников будет не меньше одного, но меньше трех, т.е. Р(1 ≤Х< 3).

Решение.

1). Построение многоугольника (полигона) распределения СВX – число опрошенных на уроке учеников приведено на рис.1.1..

Рис.1.1. Полигон распределения для данных примера 1.1.

2). Построение F(х) - функции распределения СВX – числа опрошенныхна уроке учеников.

По определению . Как следует из табл.1.2. случайная величинаХ не принимает значений, меньших 0. Следовательно, еслих < 0, то событиеX < х невозможно, а вероятность его равна нулю. Для всех значенийх, удовлетворяющих двойному неравенству 0 ≤ x < 1, функцияF(х) означает вероятность событияX < 1. Но случайная величинаX принимает значение меньшее 1 лишь в одном случае: значение 0 с вероятностью 0,1.

Если значение х удовлетворяет двойному неравенству, 0 ≤х < 2, тоF(х) = P(Х=0) + P(Х=1) = 0,1 + 0,2 = 0,3.

Пусть, например, х = 2. Тогда F(2) есть вероятность события X < 2. Это событие возможно в двух случаях: случайная величина X принимает значение 0 (с вероятностью 0,1), или 1 (с вероятностью 0,2). Применив теорему сложения вероятностей, получим F(2) = P(Х=0 и Х=1) = 0,1 + 0,2 = 0,3. Аналогичные рассуждения позволяют найти функцию распределения для данных табл. 1.1. Результат приведен в табл. 1.3.

Функция распределения (интегральная функция распределения) для примера 1.1 приведена в таблице 1.3.

Таблица 1.3

x
F(х)	0	0,1	0,3	0,6	0,8	0,9	1,0

На рис.1.2. представлен график функции распределения F(x). Функция распределенияF(x)– неубывающая функция, её значение равно единице прих, большем наибольшего возможного значения случайной величины или равном ему (рис.1.2).

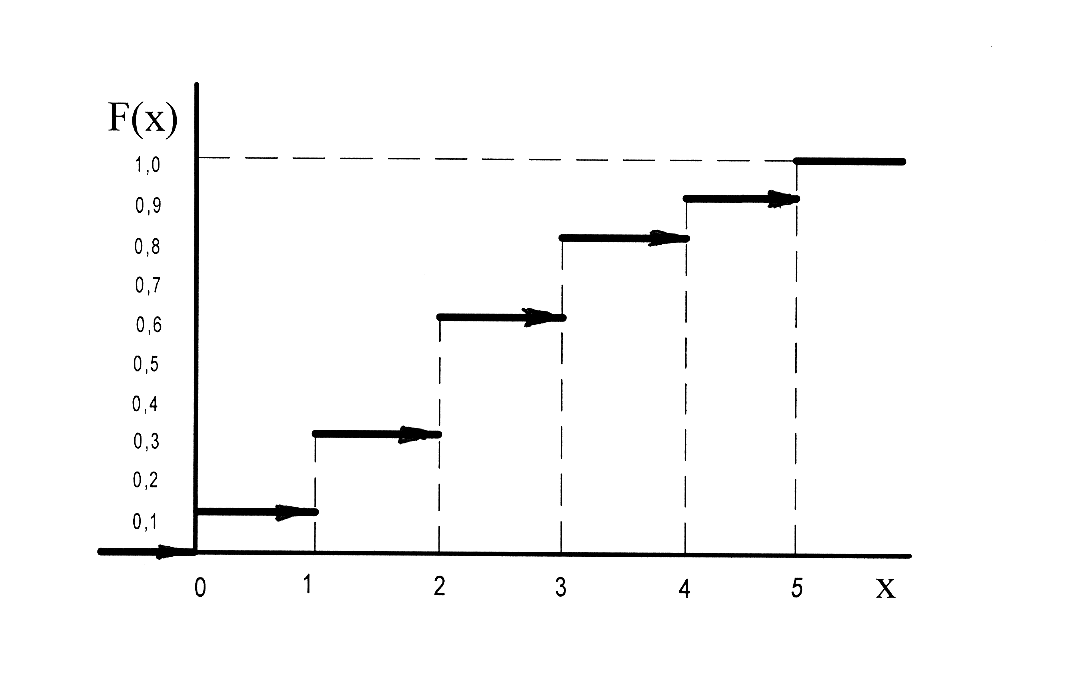
Рис.1.2. График функции распределения F(x).

График F(x) имеет ступенчатый вид. Функция распределения каждой дискретной случайной величины постоянна на интервалах и имеет скачки на границах, соответствующих значениям СВ. Величина скачков равна вероятностям конкретныxзначений СВ (табл. 1.3).

3). Как следует из таблиц 1.2. и 1.3, вероятность того, что число опрошенных на уроке учеников в определенный день будет меньше трех, можно найти по формуле Р(Х < 3) =F(3)= 0,6. С другой стороны, эту же вероятность можно найти. используяпо теорему сложения вероятностей:

Р(Х < 3) =P(Х=0 или Х=1 или Х=2)  = 0,1 + 0,2 + 0,3 = 0,6.

Вероятность того, что на уроке будет опрошено не менее одного ученика, когда вероятность события X  ≥ 1 вычисляется по формуле

P(X  ≥ 1) = 1– P(X < 1) = 1 – 0,1 = 0,9

где P(X < 1)  вероятность того, что на уроке будет опрошено менее одного ученика, т.е. не будет опрошен ни один ученик. Вероятность событияP(X  ≥ 1) также можно найти по формуле

P(X  ≥ 1) = 1– P(X < 1) = 1–F(1) = 1 – 0,1 = 0,9

Вероятность того, что число опрошенных учеников в определенный день будет не меньше одного, но меньше трех, можно найти по формуле Р(1 ≤Х <3) =F(3)–F(1) = 0,6 – 0,1 = 0,5.

Этот же результат может быть получен непосредственно по ряду распределения СВ Х(табл.1.2):

Р(1 ≤Х <3)=P(X=1)+P(X=2)=0,2+0,3=0,5