7.9. Свойства регрессионных остатков

Согласно второму условию Гаусса-Марковадля результативного применения МНК требуется, чтобы дисперсия остатков – разности значений исходных данных и данных, полученных по уравнению регрессии, былагомоскедастичной, т.е. однородной. Это значит, что для каждого значения фактораостаткиимеют одинаковую дисперсию. При малом объеме выборки для оценки гетероскедастичности (нарушении гомоскедастичности) может использоваться метод Гольдфельда-Квандта (Goldfeld-Quandt). Основная идея теста Гольдфельда-Квандта состоит в следующем:

• упорядочение nнаблюдений по возрастаниюX;

• исключение из рассмотрения Cцентральных наблюдений; при этом, где – число оцениваемых параметров;

• разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и большими значениямиХ) и определение по каждой группе уравнений регрессии;

• определение остаточной суммы квадратов для первой (S₁)и второй (S₂) групп и их отношенияF=S₁/S₂ , еслиS₁>S₂ илиF= S₂/ S₁ , еслиS₁<S₂.

При выполнении нулевой гипотезы о гомоскедастичности отношение Fбудет удовлетворятьF-критерию с числом степеней свободыдля каждой остаточной суммы квадратов. Чем больше величинаFпревышает табличное значение, тем сильнее нарушена предпосылка о равенстве дисперсий остаточных величин. Если вычисленное значениебольше, то следует учесть следующее:

• средние квадратические ошибки коэффициентов регрессии будут занижены, что может привести к ложному выводу о значимости параметров уравнения регрессии;

• полученные оценки параметров являются несмещенными оценками b_i, поэтому их можно использовать в уравнении;

• на практике стандартные ошибки пересчитываются с помощью известных методов (White,Newey-West).

Согласно третьему условию Гаусса-Марковадля корректного использования уравнения регрессии требуется, отсутствие систематической связи (корреляции) между остатками. Для исследования поведения остатков, их упорядочивают по возрастанию фактора. Остатки индексируются величинойt. Наименьшему значению фактора соответствуетt=1и остаток₁, следующему значению фактора соответствует t=2и остаток₂, и т.д. до значенияt=n.Индексtможно рассматривать как время и говорить о текущем и предшествующих моментах времени.

Автокорреляция в остатках– корреляционная зависимость между значениями остатков_t за текущий и предыдущий моменты времени. Для определения автокорреляции остатков используют критерий Дарбина-Уотсона (Durbin-Watson). Для этого вычисляют величинупо следующей формуле:

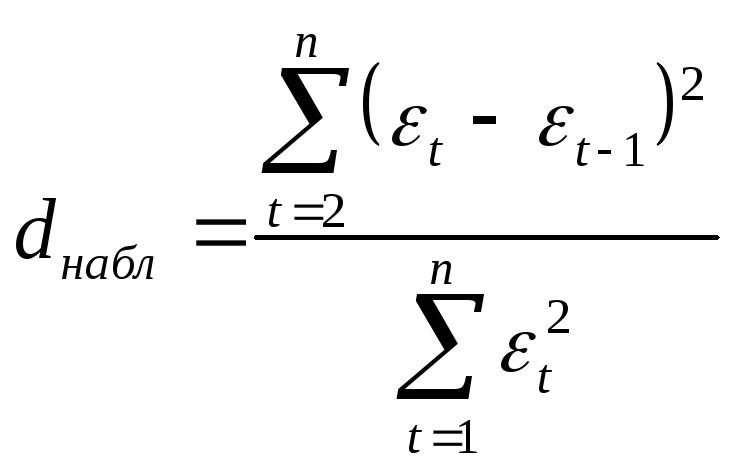, . (7.29)

где - остаток предыдущего уровня.

Для значения выполняется соотношение. По таблицам находят два критических значения: нижний уровень -и верхний -, значения которых зависит от количества наблюдений , сложности модели (количества параметров) и выбранного уровня значимости. Если превышает 2, то это свидетельствует об отрицательной корреляции и перед сравнением его величину надо преобразовать:.

Если - модель неадекватна, остатки сильно автокоррелированы.

Если -остатки некоррелированы, модель адекватна.

Если - однозначного вывода сделать нельзя и необходимо применять другие критерии.

Если в остатках полная положительная автокорреляция, то , если полная отрицательная, то, если автокорреляция остатков отсутствует, то.

Если обнаружена автокорреляция, то, как и в случае с гетероскедастичностью, следует помнить: стандартные ошибки будут занижены, что может привести к ложному выводу о значимости коэффициентов уравнения регрессии. При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный МНК заменять обобщенным методом (ОМНК), который применяется к преобразованным данным.

Весьма вероятна положительная автокорреляция остатков. Н0 отклоняется.	Зона неопределенности	Нет оснований отклонять Н0. Автокорреляция остатков отсутствует.	Зона неопределенности	Весьма вероятна отрицательная автокорреляция остатков.Н0 отклоняется.
0 dL dU 2 4-dU 4-dL 4

Рис.7.3 Области принятия и непринятия гипотезы об автокорреляции остатков.