7.4. Скорректированный индекс множественной детерминации

Скорректированный (исправленный, adjustable) коэффициент множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле :

(7.23)

Скорректированный коэффициент множественной детерминации используется для сопоставления моделей содержащих различное количество факторов.

Чем больше p, тем больше различие междуи . Чем больше объем выборкиn, тем меньше это различие.

Существенно различным может быть изменение и при включении дополнительного фактора в уравнение регрессии. Если этот фактор существенно влияет на отклик, то увеличатся значения как так и . Если вновь добавленный фактор несущественно влияет на отклик, то значение , как правило, увеличивается (может быть незначительно), а значение- уменьшается. Очевидно, что в этом случае такой фактор в уравнение включать не целесообразно.

7.5. Частная корреляция

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на факторапри устранении влияния других факторов, включенных в уравнение регрессии, можно определить по формуле:

, (7.24)

где - коэффициент детерминированности для уравнения регрессии, в которое включены факторы;- коэффициент детерминированности для уравнения регрессии, в которое включены факторы, т.е. факторисключен из уравнения. Частные коэффициенты корреляции изменяются в пределах от0до1.

Нетрудно показать, что величина, стоящая под радикалом в правой части равенства (7.24) может быть преобразована к следующему виду:

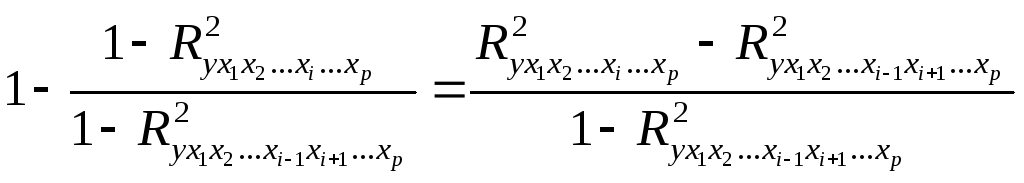
Правая часть последнего равенства представляет собой отношение приращения объясненной часть вариации отклика за счет включения фактора в уравнение регрессии к необъясненной доле вариации отклика, имевшей место до введения факторав уравнение регрессии.

Таким образом, величина характеризует возрастание коэффициента детерминации за счет введения в уравнение регрессии фактора. Благодаря этому частные коэффициенты корреляции могут быть использованы для ранжирования влияния факторов на результат.

Так, при двух факторах и i=1 частный коэффициент корреляцииможет быть вычислен по формуле

(7.25)

Коэффициент показывает тесноту связи междуипри неизменном уровне фактора, включенного в уравнение регрессии.

Аналогично можно определить по формуле

(7.26)

Коэффициенты частной корреляции используют для оценки целесообразности включения фактора в уравнение регрессии.

7.6. Геометрическая интерпретация

В основном совпадает с геометрической интерпретацией регрессионного уравнения с одной переменной, приведенной в ЛР №5 [1]. Столбцы значений представим как векторы вp+1-мерном векторном пространствоR^p+1.

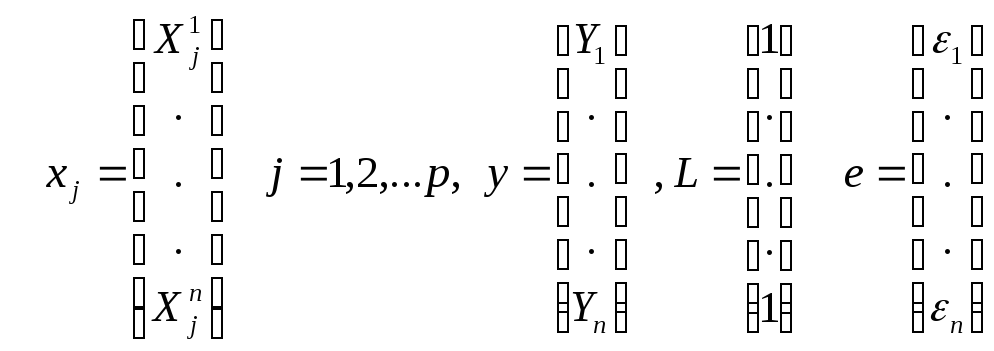
Векторы порождаютp+1–мерное подпространствоπ(рис.7.1). Рассмотрим векторыи, определяемые следующими соотношениями

(7.27)

Очевидно, что вектор лежит в гиперплоскости (подпространстве)π.

Поставим задачу: найти такие , чтобы векторeимел наименьшую длину. Другими словами мы хотим наилучшим образом аппроксимировать векторy вектором, лежащим в гиперплоскостиπ. Очевидно, что решением является такой вектор, для которого векторeортогонален (перпендикулярен) плоскостиπ. Для этого необходимо и достаточно, чтобы векторeбыл ортогонален векторами, порождающим плоскостьπ (рис. 5.3). Т.е. векторявляется ортогональной проекцией векторана плоскостьπ. Вектор остатковортогоналенπ.

Рис. 7.1Геометрическая интерпретация построения уравнения регрессии

Т.е. фактически актуален рис.5.3 ЛР №5 [1]с заменой векторов, порождающих гиперплоскость π.