РГЗ №1
.docx
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ
«ГОРНЫЙ»
Кафедра общей и технической физики
Расчётно-графическое задание №2
Вариант №15
Тема: «Движение тела, брошенного под углом к горизонту»
Выполнил: студент гр. ПМК-13 _____________ /Некрасова Е.А./
(подпись) (Ф.И.О.)
Проверил: доцент _____________ /Левин К.Л./
(подпись) (Ф.И.О.)
Санкт-Петербург
2013 г.
Задание
Тело массой m=1 кг брошено под углом α=42 ̊ к горизонту со скоростью V0=35 м/с.
Определить:
В момент времени t1=ktв значение дальности полёта L и радиус кривизны траектории R.
Построить:
-
Графическую зависимость угла β, под которым направлена скорость к горизонту от времени в процессе всего движения тела – β(t).
-
Траекторию движения тела с указанием на ней положения тела в момент времени
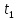 .
.
Краткие теоретические сведения
Баллистика – раздел механики, изучающий движение тел в поле тяжести Земли. Баллистическое движение совершают снаряды, пули, футбольные мячи, теннисные мячи и т.п.
При описании баллистического движения:
-
тело рассматривают как материальную точку
-
сопротивление воздуха не учитывают
Баллистическое движение представляет собой свободное падение с постоянным ускорением свободного падения g=const.
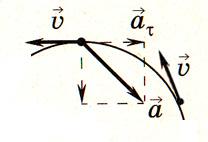
Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение тела, брошенного под углом к горизонту, представляет комбинацию двух движений (рис. 1):
-
равномерное движение вдоль горизонтальной оси (оси Х);
-
равнопеременное движение вдоль вертикальной оси (оси Y) с ускорением
 .
.
Определение физических величин
Скорость - векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта.
В системе СИ - (м/с).
Перемещение - изменение местоположения физического тела в пространстве, относительно выбранной системы отсчёта.
В системе СИ - (м).
Сила - векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей.
В системе СИ - (Н).
Ускорение - производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени.
В системе СИ - (м/с²).
Ускорение свободного падения - ускорение, придаваемое телу в вакууме силой тяжести. В соответствии со вторым законом Ньютона, ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Значение ускорения свободного падения на поверхности Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с², а в технических расчётах обычно принимают g = 9,81 м/с².
В системе СИ - (м/с²).
Траектория - это линия, вдоль которой движется тело.
В системе СИ - (м).
Путь - это сумма длин всех участков траектории, последовательно проходимых телом при движении.
В системе СИ - (м).
Расчётные формулы
Проекции скорости тела изменяются со временем следующим образом:
![]()
где ![]() –
начальная скорость, α – угол бросания.
–
начальная скорость, α – угол бросания.
Координаты тела изменяются так:
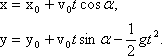
При нашем выборе начала координат
начальные координаты
![]() ,
тогда имеем:
,
тогда имеем:
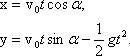
Время движения брошенного тела:
![]()
Дальность полета – это значение координаты х в конце полета:
![]()
Максимальная высота подъема брошенного тела:
![]()
Уравнение траектории движения:
![]()
|
Тангенциальное ускорение: |
![]()
Нормальное ускорение:
![]()
R - радиус кривизны траектории в данной точке.
Модуль полного ускорения:
![]()
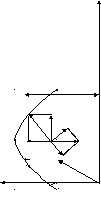
Решение
В момент времени t1=ktв значение дальности полёта L и радиус кривизны траектории R .
-
Для того чтобы определить момент времени , определим общее время полета тела . Это время равно:
;
.
-
Дальность полёта в момент времени
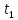 определяется по формуле:
определяется по формуле:
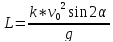

-
Радиус кривизны в момент времени
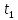 определяется по формуле:
определяется по формуле:
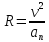
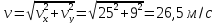
 м/с
м/с
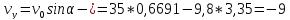 м/с
м/с
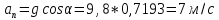

-
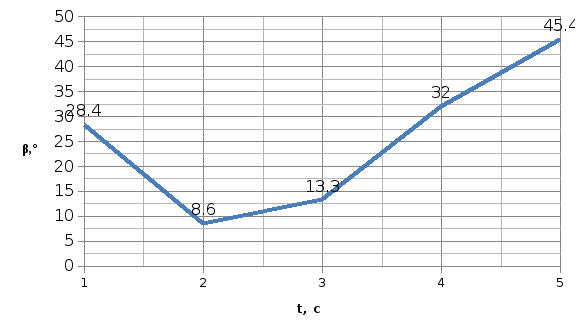
Для того чтобы построить графическую зависимость угла β, под которым направлена скорость к горизонту от времени в процессе всего движения тела - β(t) - нужно знать следующие величины:
|
t, с |
|
|
β, |
|
1 |
25,1755 |
13,6185 |
28,4 |
|
2 |
25,1755 |
3,8185 |
8,6 |
|
3 |
25,1755 |
-5,9815 |
13,3 |
|
4 |
25,1755 |
-15,7815 |
32 |
|
5 |
25,1755 |
-25,5815 |
45,4 |
График зависимости β(t)
-
Для того чтобы построить траекторию движения тела с указанием на ней положения тела в момент времени
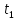 нужно знать следующие величины:
нужно знать следующие величины:
|
X, м |
Y, м |
|
25 |
18,5 |
|
50 |
27,2 |
|
75 |
26,15 |
|
84 |
23,4 |
|
100 |
15 |
|
125 |
-5,4 |
Траектория движения
тела с указанием на ней положения тела
в момент времени
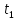

Вывод
В данной работе исследовалось движение тела, брошенного под углом к горизонту. Рассчитаны требуемые значения:
-
Дальность полета тела равна

-
Радиус кривизны траектории тела
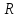 =
=
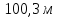
Показан график зависимости угла, под которым направлена скорость к горизонту от времени.
Построена траектория
движения тела с указанием на ней положения
тела в момент времени
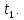

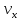 ,
м
,
м ,
м
,
м