
к.р. моя - гидрогазодинамика
.docxЗадача 1. В трубе диаметром D1 = 50 мм, подающей воду в открытый бак с постоянным напором Н, установлена труба Вентури с диаметром горла D2 = 25 мм. Атмосферное давление pа = 100 кПа.
Определить, какой наибольший расход можно подавать в бак до появления кавитации в расходомере, если температура воды t. Каково будет при этом показание ртутного дифманометра ∆h?
Дано:
D1 = 50 мм = 0,05 м
D2 = 25 мм = 0,025 м
Pа = 100 кПа
H = 0,8 м
t = 60оС
Решение:
Применим уравнение Бернулли к выбранным сечениям потока несжимаемой жидкости и пренебрежем поначалу потерями напора между ними:
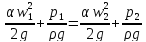
Уравнение неразрывности wF = const позволяет выразить w1 через w2:
w1
=
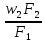 =
=
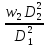
Подставляя значения w в уравнение Бернулли, имеем:
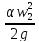

 =
=
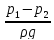 – H
– H
где F = 0,785d2,
α = 1,1 (для турбулентного режима),
ρ = 983,2 кг/м3 (при t = 60оС),
p2 = 19946 Па (давление насыщения пара при t = 60оС).
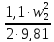

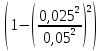 =
=
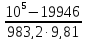 – 0,8
– 0,8
0,056w22
 0,9375 = 8,3 – 0,8
0,9375 = 8,3 – 0,8
0,0525w22 = 7,5
w2
=
 = 11,95 м/с
= 11,95 м/с
Отсюда расход, вычисляемый по средней скорости в сжатом сечении, равен:
Q = w2F2
Q
= 11,95
 0,785
0,785
 0,0252
= 5,86
0,0252
= 5,86
 10-3
м3/с
10-3
м3/с
Ответ:
Q
= 5,86
 10-3
м3/с
10-3
м3/с
Задача 2. Из открытого бака вода вытекает в атмосферу по горизонтальному трубопроводу, составленному из труб диаметром D1 и D2, длины которых l1 = 20 м, l2 = 40 м. Трубы стальные новые, высота выступов шероховатости 0,1 мм, толщина стенки 3 мм. Расход воды Q, коэффициенты местного сопротивления: входа ζвх = 0,5, резкого расширения ζрр = [(D1/D2)2 – 1]2, крана ζкр = 1,0. Определить напор в баке H и величину ударного давления ∆p при мгновенном закрытии крана. Построить диаграмму уравнения Бернулли. Гидравлический коэффициент трения определить по графику приложения.
Дано:
D1 = 30 мм
D2 = 50 мм
l1 = 20 м
l2 = 40 м
Q = 4 ∙ 10-3 м3/с
ζвх = 0,5
ζрр = [(D1/D2)2 – 1]2
ζкр = 1,0
δ = 3 мм
∆ = 0,1 мм
Решение:
Составляя уравнение Бернулли, имеем:
H =
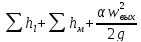 ,
,
где
 = hl1
+ hl2
= λтр1
= hl1
+ hl2
= λтр1
 + λтр2
+ λтр2

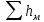 =
=
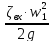 +
+

Подставляя эти значения в первое уравнение и выражая скорость w1 через w2 из уравнения неразрывности, имеем:
H =

w2
=
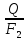 =
=
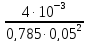 = 2,04 м/с
= 2,04 м/с
w1
=
 =
=
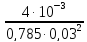 = 5,66 м/с
= 5,66 м/с
Определим гидравлические коэффициенты трения по относительной шероховатости труб и числу Re:
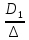 =
=
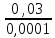 = 300
= 300
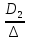 =
=
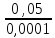 = 500
= 500
ν
= 1,006
 10-6
м2/с
(кинематическая вязкость воды при 20оС).
10-6
м2/с
(кинематическая вязкость воды при 20оС).
Re1
=
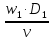 =
=
 = 168787 = 1,7
= 168787 = 1,7
 105
105
Re2
=
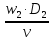 =
=
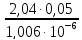 = 101391 = 1,0
= 101391 = 1,0
 105
105
Отсюда: λтр1 = 0,027; λтр2 = 0,024
H
=
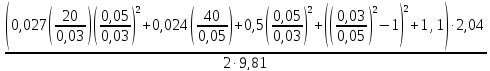 = 7,5 м
= 7,5 м
Величина ударного давления:
 p
= ρ
p
= ρ
 w2
w2
 c,
c,
где ρ = 1000 кг/м2
с =
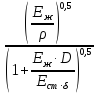 ,
,
где
Еж
= 2,1
 109
Па – модуль Юнга жидкости, Ест
= 2
109
Па – модуль Юнга жидкости, Ест
= 2
 1011
Па – модуль Юнга стали.
1011
Па – модуль Юнга стали.
с =
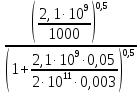 = 1337 м/с
= 1337 м/с
 p
= 1000
p
= 1000
 2,04
2,04
 1337 = 2,7 МПа
1337 = 2,7 МПа
Ответ: H = 7,5 м
 р
= 2,7 МПа
р
= 2,7 МПа
Задача 3. В конденсаторе паротурбинной установки охлаждающая вода проходит по двум последовательным ходам, каждый из которых содержит 250 параллельных латунных трубок длиной L = 5 м и внутренним диаметром D = 14 мм; размер выступов шероховатости 0,05 мм.
Определить потери напора в конденсаторе, если расход равен Q, температура воды t. Учитывать потери напора на трение в трубках, на вход (ζвх = 0,5) и на выход (ζвых = 1,0). Использовать график приложения для определения λ.
Дано:
n = 250
L = 5 м
D = 14 мм = 0,014 м
∆ = 0,05 мм
Q = 590 м3/ч = 0,164 м3/с
t = 30оС
ζвх = 0,5
ζвых = 1,0
Решение:
Определяем скорость воды в трубках:
w
=
 =
=
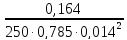 = 4,26 м/с
= 4,26 м/с
Потеря напора вычисляется по формуле:
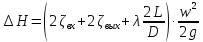 ,
,
где
ν = 0,833
 10-6
м2/с
10-6
м2/с
Определим гидравлические коэффициенты трения по относительной шероховатости труб и числу Re:
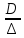 =
=
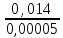 = 280
= 280
Re
=
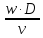 =
=
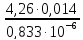 = 71597 = 7,16
= 71597 = 7,16
 104
104
Отсюда λ = 0,0275
 H
=
H
=
 = 20,9 м
= 20,9 м
Ответ:
 H
= 20,9 м
H
= 20,9 м
Задача 4. Воздух вытекает из баллона через сужающееся сопло диаметром D в атмосферу, атмосферное давление 100 кПа. Температура в баллоне 400 К, избыточное давление pизб. Определить скорость истечения, массовый расход и параметры воздуха на срезе сопла. Определить также скорость и параметры воздуха на выходе и диаметр выходного сечения сопла Лаваля, которое обеспечивает расчетное истечение и имеет диаметр горла D.
Дано:
D = 5 мм = 0,005 м
pизб = 7 МПа
Т = 400 К
pатм = 100 кПа
Решение:
1. Так как p меньше pкр, скорость истечения равна критической скорости:
акр
=
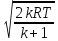 =
=
 = 366 м/с,
= 366 м/с,
где k = 1,4 – показатель адиабаты
R
= 287 Дж/кг К
К
Массовый секундный расход:
G
=
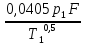 =
=
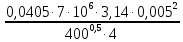 = 0,278 кг/с
= 0,278 кг/с
Удельный объем:
ν1
=
 =
=
 = 0,0164 м3/кг
= 0,0164 м3/кг
2. Истечение из сопла Лаваля:
По
значению π =
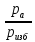 = 0,0143 из таблицы находим:
= 0,0143 из таблицы находим:
λ = 2,05
τ = 0,2996
ε = 0,0491
q = 0,1588
Соответственно:
w
= λaкр
= 2,05 366
= 750 м/с
366
= 750 м/с
T
= τT1
= 0,2996
 400 = 120 К
400 = 120 К
Так
как процесс истечения адиабатический,
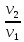 =
=
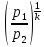 ,
отсюда:
,
отсюда:
ν2
= 0,0164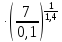 = 0,341 м3/кг
= 0,341 м3/кг
 =
=
 , отсюда:
, отсюда:
T2
=
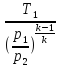 =
=
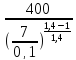 = 119 К
= 119 К
Площадь выходного сечения, обеспечивающего расчетное истечение:
F
=
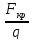 =
=
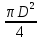 , диаметр сопла Лаваля на выходе:
, диаметр сопла Лаваля на выходе:
D
=
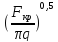 =
=
 =
=
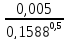 = 0,013 м
= 0,013 м
Ответ: акр = 366 м/с
G = 0,278 кг/с
w = 750 м/с
D = 0,013 м
Задача 5. Плоская тонкая квадратная пластинка с размером стороны b обтекается продольно потоком воздуха нормальных параметров. Скорость потока w.
Вычислить толщину пограничного слоя у выходной кромки пластинки и определить силу сопротивления.
Дано:
b = 0,8 м
w = 70 м/с
Решение:
Re
=
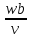 =
=
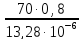 = 4216867 ,
= 4216867 ,
где
ν = 13,28
 10-6
м2/с
– кинематическая вязкость воздуха при
нормальных условиях
10-6
м2/с
– кинематическая вязкость воздуха при
нормальных условиях
Толщина пограничного слоя для турбулентных потоков:
δ =
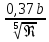 =
=
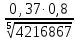 = 0,014 м
= 0,014 м
Полная сила трения на одной стороне пластинки равна:
Rтр1
= СтрF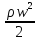 =
=
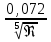
 b2
b2

 =
=

 0,82
0,82

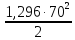 = 6,9 Н,
= 6,9 Н,
где ρ = 1,296 кг/м3 – плотность воздуха
Общее сопротивление пластины:
Rтр
= 2 Rтр1
= 2 6,9 = 13,8 Н
6,9 = 13,8 Н
Ответ: δ = 0,014 м
Rтр = 13,8 Н
Задача 6. Активная решетка прямых турбинных лопаток обтекается потоком воздуха. Угол входа потока β1 = 19,5о, угол выхода β2 = 20,6о, хорда лопатки b = 25,7 мм, относительный шаг решетки t = t/b = 0,6.
Определить параметры потока за решеткой, силы, действующие на одиночную лопатку, и построить диаграмму сил.
Дано:
p1 = 2,65 МПа
p2 = 2,5 МПа
w1 = 225 м/с
T1 = 635 К
β1 = 19,5о
β2 = 20,6о
b = 25,7 мм
t = t/b = 0,6
Решение:
Плотность воздуха на входе:
ρ1
=
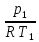 =
=
 = 14,54 кг/м3
= 14,54 кг/м3
Удельный объем:
ν1
=
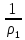 =
=
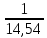 = 0,069 м3/кг
= 0,069 м3/кг
Процесс расширения – адиабатный, параметры воздуха на выходе из решетки:
ρ2
= ρ1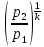 = 14,54
= 14,54
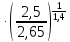 = 13,95 кг/м3
= 13,95 кг/м3
ν2
=
 =
=
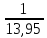 = 0,072 м3/кг
= 0,072 м3/кг
T2
= T1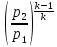 = 635
= 635

 = 624,5 К
= 624,5 К
Уравнение неразрывности:
ρ1w1a = ρ2w2a или ρ1w1sinβ1 = ρ2w2sinβ2
Отсюда:
w2a
=
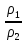 w1a
=
w1a
=
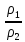 w1sinβ1
=
w1sinβ1
=

 225
225
 sin19,5 = 78,3 м/с
sin19,5 = 78,3 м/с
w2
=
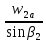 =
=
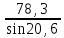 = 222,5 м/с
= 222,5 м/с
w1a
= w1sinβ1
= 225
 sin19,5 = 75,1 м/с
sin19,5 = 75,1 м/с
Аэродинамические силы, действующие на лопатку метровой длины:
t
= 0,6b = 0,6
 25,7 = 15,4 мм
= 0,0154 м
25,7 = 15,4 мм
= 0,0154 м
Pu
= ρ1w1at
(w1u
–(- w2u))
= 14,54 75,10,0154
75,10,0154
 (225cos19,5 –(- 222,5cos20,6)) = 6532 Н/м
(225cos19,5 –(- 222,5cos20,6)) = 6532 Н/м
Pa
= ρ1w1at
(w1a
- w2a)
+ t(p1
– p2)
= 14,54 75,10,0154
75,10,0154
 (75,1 – 78,3) + 0,0154
(75,1 – 78,3) + 0,0154
 (2,65
(2,65
 106
– 2,5
106
– 2,5
 106)
= 2260 Н/м
106)
= 2260 Н/м
Ответ: Pu = 6532 Н/м
Pa = 2260 Н/м
