Лаба 7 отчёт

Министерство общего и специального образования

Санкт-Петербургский Национальный Минерально-Сырьевой университет

"Горный".

Отчёт по лабораторной работе № 7.

По дисциплине: Физика

(наименование учебной дисциплины согласно учебному плану)

Тема: Исследование метрологических возможностей моста Уитстона

Выполнил: студент гр. ГГ-13-1 ___________ Куприянов В.О.

^{(подпись) (Ф.И.О.)}

Дата: __________________

ПРОВЕРИЛ:

Доцент: ____________ Дьяконов К.В.

^{(подпись) (Ф.И.О.)}

Санкт-Петербург

2014 год

Цель работы: Изучение метрологических возможностей мостовой схемы. Определение удельного сопротивления заданного материала.

Краткое теоретическое содержание

В технике мост Уитстона, благодаря своей высокой чувствительности и большой точности, применяется в основном в контрольно- измерительной аппаратуре. Например, для определения изменения сопротивления тензорезистора (тензодатчика), “измеряющего” изменение давления, температуры, распределение деформаций (изгиб или сжатие-растяжение) в конструктивных элементах зданий, сооружений, в сводах подземных выработок и т.д. Причем, из-за высокой чувствительности мостика к дисбалансировке, тензочувствительность датчиков настолько высока, что позволяет измерять даже микродислокации (микродавления и т.п.) в исследуемом объекте. Использование «метода мостика» является одним из распространенных способов измерения различных физических параметров электрических цепей: сопротивлений, емкостей, индуктивностей и др. Изучение закономерностей работы мостовой схемы позволит обобщить приобретенные знания и успешно использовать их как в лабораторных условиях, так и в производстве.

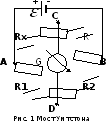
Принципиальная схема метода мостика Уитстона дана на рис. 1.

Кроме того, мост Уитстона мало подвержен влиянию электромагнитных помех, т.к. индуцируемые ими в левой и правой частях схемы токи в диагонали моста компенсируются. Измеряемое сопротивление R_x и три других переменных сопротивления R, R₁ и R₂ соединяются так, что образуют замкнутый четырехугольник ABCD. В одну диагональ четырехугольника включен гальванометр G (этот участок и является мостиком), а в другую диагональ включен источник постоянного тока . При произвольных значениях всех сопротивлений гальванометр покажет наличие тока на участке CD. Но можно подобрать сопротивления R, R₁ и R₂ так, что ток в цепи гальванометра будет равен нулю. В этом случае потенциалы точек C и D будут равны (_C = _D), а через сопротивления R₁ и R₂ будет идти ток I₁, и через сопротивления R_x и R будет идти ток I_x. Тогда по закону Ома для каждого участка цепи можно записать следующие уравнения:

_A – _C = I_x  R_x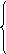

_A – _D = I₁  R₁

_C – _B = I_x  R

_D – _B = I₁  R₂

Учитывая, что _C = _D, получим:

I_x  R_x = I₁  R₁

I_x  R = I₁  R₂

Разделив уравнение (2) на уравнение (3), получим:

.

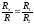Таким образом, искомое сопротивление:

.

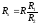На практике часто используют схему так называемого линейного или струнного моста Уитстона (рис. 2). Сопротивления R₁ и R₂ в этой схеме лежат на одной прямой и вместе представляют собой однородную проволоку (струну), по которой на скользящем контакте перемещается движок D, соединенный с гальванометром G. Линейку вместе с укрепленной на ней струной и движком называют реохордом. 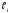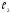Вследствие того, что проволока реохорда однородна и тщательно откалибрована (имеет везде одинаковое поперечное сечение), отношение сопротивлений участков цепи AD (сопротивление R₁) и DB (сопротивление R₂) можно заменить отношением соответствующих длин плеч реохорда и (на основании прямо пропорциональной зависимости ): .

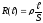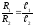Тогда окончательная формула для определения искомого сопротивления имеет вид:

.

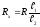В общем виде для разветвленных цепей (к коим относится и мостовая схема Уитстона) в установившемся режиме применимы два правила Кирхгофа:

1-ое правило Кирхгофа для любого узла цепи имеет вид:

,

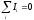где I_i – значения токов втекающих в данный узел и вытекающих из него. Ток принято считать отрицательным, если он вытекает из данного узла.

2-ое правило Кирхгофа для каждого замкнутого контура в сети линейных проводников:

,

где I_i – значение тока, протекающего через сопротивление i-ого проводника R_i, 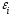– ЭДС i-ого источника в данном контуре. При этом, ток считается положительным, если направление обхода по контуру совпадает с направлением тока; э.д.с. считается положительной, если при обходе контура “проходим” от отрицательной клеммы к положительной.

Кроме того, можно измерить общее сопротивление двух и более проводников, подключенных вместо сопротивления R_x в его контакты либо последовательно, либо параллельно. В этом случае результирующее сопротивление для последовательного соединения:,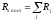

а для резисторов, соединенных параллельно:

.

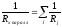Таким образом, если установить вместо R на рис. 2 известное сопротивление и точно измерить по линейке расстояния 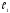и 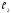, отвечающие I_G = 0, можно определить неизвестное сопротивление R_x, включенное в схему моста. Известно, что реохордный мост Уитстона обладает наибольшей чувствительностью, когда движок стоит на середине струны. Точное определение R_x позволяет найти значение удельного сопротивление проводника, в том числе неизвестного сплава, по формуле:

.

Электрическая схема:

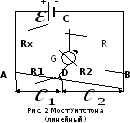
Расчетные формулы:

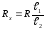
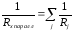
Формулы погрешностей косвенных измерений:

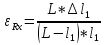
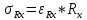
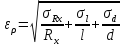
Таблица № 1 Измерение неизвестного сопротивления.

R (Ом)	l1 (м)	l2 (м)	Rx (Ом)
10	0,920	0,080	115
50	0,668	0,332	100,6
100	0,502	0,498	100,8

Талица № 2 Определение удельного сопротивления материала проволоки № 1.

d=1

R (Ом)	l1 (м)	l2 (м)	Rx (Ом)	ρ (мкОм*м)
10	0,058	0,942	0,615	0,484
50	0,005	0,995	0,251	0,197

Таблица № 3 Определение удельного сопротивления материала проволоки № 2. d=0.5

R (Ом)	l1 (м)	l2 (м)	Rx (Ом)	ρ (мкОм*м)
10	0,2	0,8	2,5	0,491
50	0,040	0,960	2,083	0,409
100	0,015	0,985	1,523	0,299

Таблица № 4 Измерение сопротивления проволок при их последовательном соединение.

R (Ом)	l1 (м)	l2 (м)	Rx,послед (Ом)
10	0,236	0,764	3,089
50	0,048	0,952	2,521
100	0,017	0,983	1,729

Таблица № 5 Измерение сопротивления проволок при параллельном соединении.

R (Ом)	l1 (м)	l2 (м)	Rx,парал (Ом)
10	0,040	0,960	0,417
50	0,003	0,997	0,150

Пример вычисления.

Исходные данные:

l₁ = 0,502 (м) l₂ = 0,498 (м) R =100 (Oм)

Вычисления:

R_x=(0,502*100)/0,498=100,8 Ом

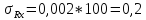
Результат вычислений:

R_x=100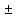0,2 Ом.

Результаты опытов и вычислений:

R_x=105,46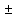0,21 Ом

ρ₁=0,340 0,073 мкОм*м

ρ₂=0,399 0,071 мкОм*м

R_{x,послед} =2,446 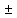0,011 Ом

R_x,парал =0,2830,01 Ом

Заключение.

Мост Уитстона является эффективным прибором для нахождения сопротивления и прочих связанных с ним значений. Полученные результаты отличаются от справочных на 20-30%, причиной такой погрешности является неточность установки и человеческий фактор. При проведении опыта было достигнуто близкое удельного сопротивления к действительному. Наименьшая погрешность была достигнута при измерении с сопротивлением =10 Ом. Реальное около 0,5*10^-6.