
- •Курсовая работа
- •Пояснительная записка
- •Кафедра Информатики и компьютерных технологий курсовая работа
- •Задание
- •Аннотация
- •The summary
- •Оглавление
- •Введение
- •1 Расчет неприступного расстояния
- •Теорема синусов для треугольника авс1:
- •2 Решение прямой угловой засечки по формуле Юнга
- •3 Решение прямой угловой засечки по формулам Гаусса
- •4. Решение обратной угловой засечки по формулам Пранис-Праневича
- •Заключение
- •Список литературы
2 Решение прямой угловой засечки по формуле Юнга
В данной задаче
необходимо было рассчитать координаты
 ,
,
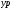 удаленной точки
P,по формулам Юнга
(рис. 5). Даны точки 1 и 2 с координатами
удаленной точки
P,по формулам Юнга
(рис. 5). Даны точки 1 и 2 с координатами
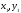 и
и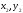 соответственно. Кроме этого с помощью
угломерного инструмента измерены углы
соответственно. Кроме этого с помощью
угломерного инструмента измерены углы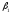 и
и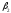 .
Стоит обратить внимание, что при решении
геодезических задач в отличии от
общепринятых вычислений оси координат
0x
и 0y
переставлены местами.
.
Стоит обратить внимание, что при решении
геодезических задач в отличии от
общепринятых вычислений оси координат
0x
и 0y
переставлены местами.
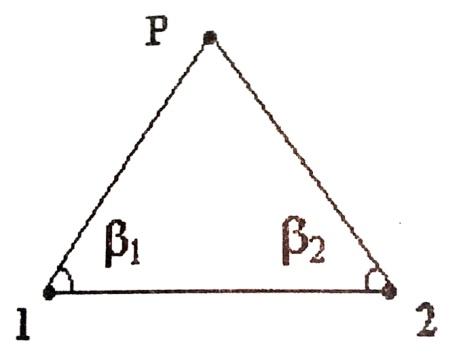
Рис. 6. Схема расчета координат по формулам Юнга
Для вычисления координат удаленной точки P использовались следующие расчетные формулы:
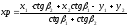 ,
,
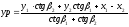 .
.
Сначала задача была решена средствами МS Excel. Результат представлен на рис. 7.

Рис. 7. Рабочее окно MSExcelпри расчете координаты по формулам Юнга.
Результат вычисления
координат точки Р
в МS
Excel
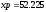 м,
м,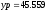 м.
м.
Затем решение осуществлялось средствами MathCAD. В результате чего был получен следующий вид вычисления координат точки Р:

Рис. 8. Рабочее окно MathCadпри расчете координаты по формулам Юнга.
Результат вычисления
координат точки Р
в MathCAD
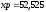 м,
м,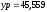 м.
м.
Далее решение выполнялось средствами MatLab. Результат представлен на рис. 7.
Программный код:
clc
x1=input('x1->');
y1=input('y1->');
x2=input('x2->');
y2=input('y2->');
b1g=input('b1(grad)->');
b1m=input('b1(min)->');
b1s=input('b1(sec)->');
b2g=input('b2(grad)->');
b2m=input('b2(min)->');
b2s=input('b2(sec)->');
b1=b1g+b1m/60+b1s/3600;
b2=b2g+b2m/60+b2s/3600;
b1=b1*pi/180;
b2=b2*pi/180;
xp = (x1*cot(b2)+x2*cot(b1)-y1+y2)/(cot(b1)+cot(b2))
yp = (y1*cot(b2)+y2*cot(b1)+x1-x2)/(cot(b1)+cot(b2))
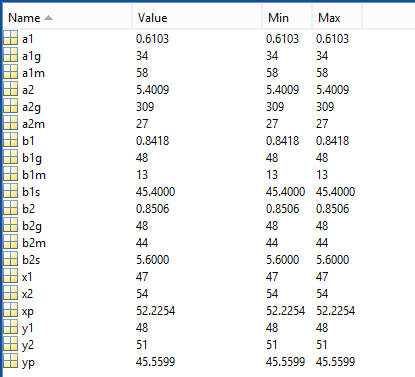

Рис. 9. Рабочее окно MatLabпри расчете координаты по формулам Юнга.
Результат вычисления
координат точки Р
в MatLab
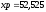 м,
м,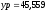 м.
м.
Решение данной задачи завершалось вычислением координат точки Р средствами Visual Basic 6.0. Был получен следующий вид решения, результат которого представлен на рис. 8.
Программный код:
Functionctg(x)
ctg=Cos(x) /Sin(x)
EndFunction
PrivateSubCommand1_Click()
Cls
X1 = Val(Text1(0).Text): Y1 = Val(Text2.Text)
X2 = Val(Text6.Text): Y2 = Val(Text7.Text)
b1 = Val(Text3.Text) + Val(Text4.Text) / 60 + Val(Text5.Text) / 3600
b2 = Val(Text8.Text) + Val(Text9.Text) / 60 + Val(Text10.Text) / 3600
pi = 3.1415926
b1 = b1 * pi / 180
b2 = b2 * pi / 180
xp = (X1 * ctg(b2) + X2 * ctg(b1) - Y1 + Y2) / (ctg(b1) + ctg(b2))
yp = (Y1 * ctg(b2) + Y2 * ctg(b1) + X1 - X2) / (ctg(b1) + ctg(b2))
Print "xp="; xp, "yp="; yp
End Sub
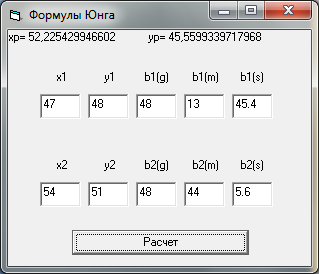
Рис. 10. Рабочее окно VisualBasicпри расчете координаты по формулам Юнга.
Результат вычисления
координат точки Р
в Basic
6.0 приблизительно
 м,
м, м.
м.
Таким образом, среднее значение координат точки Р, рассчитанных по формулам Юнга, оказались равныxp=52.225 м yp=45.559 м.
3 Решение прямой угловой засечки по формулам Гаусса
В данной задаче
необходимо было вычислить координаты
удаленной точки P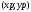 ,
по координатам двух заданных точек 1
,
по координатам двух заданных точек 1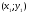 и 2
и 2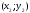 и дирекционным углам
и дирекционным углам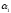 и
и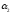 (рис. 11).
(рис. 11).
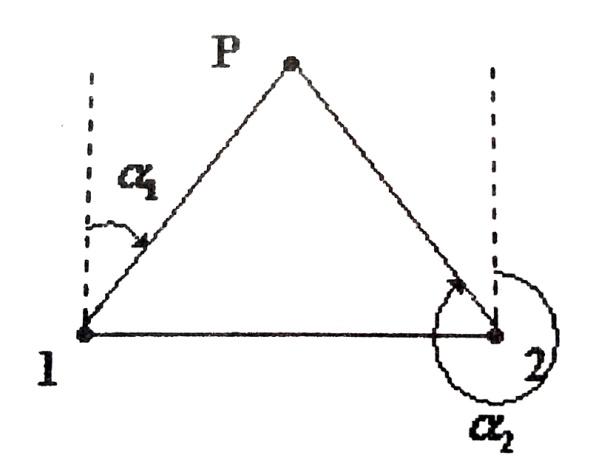
Рис. 11. Схема для вычисления координат по формулам Гаусса
Для вычисления координат удаленной точки P использовались формулы Гаусса:
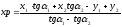 ,
,
 .
.
Сначала задача была решена средствами МS Excel. Результат представлен на рис. 12
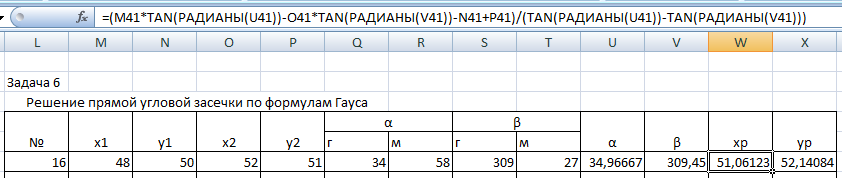
Рис. 12. Рабочее окно MSExcelпри расчете прямой угловой засечки по формулам Гаусса.
Результат вычисления
координат точки Р
в МS
Excel
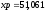 м,
м,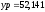 м.
м.
Затем решение осуществлялось средствами MathCAD. В результате чего был получен следующий вид вычисления координат точки Р:

Рис. 12. Рабочее окно MathCadпри расчете прямой угловой засечки по формулам Гаусса.
Результат вычисления
координат точки Р
в MathCAD
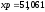 м,
м,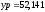 м.
м.
Далее решение выполнялось средствами MatLab. Результат представлен на рис. 11.
Программный код:
clc
x1=input('x1->');
y1=input('y1->');
x2=input('x2->');
y2=input('y2->');
ag=input('a(grad)->');
am=input('a(min)->');
bg=input('b(grad)->');
bm=input('b(min)->');
a=ag+am/60;
b=bg+bm/60;
b=b*pi/180;
a=a*pi/180;
xp = (x1*tan(a)-x2*tan(b)-y1+y2)/(tan(a)-tan(b))
yp = y1+(xp-x1)*tan(a)
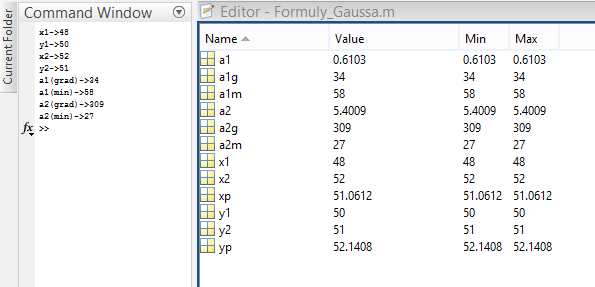

Рис. 12. Рабочее окно MatLabпри расчете прямой угловой засечки по формулам Гаусса.
Результат вычисления
координат точки Р
в MatLab
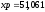 м,
м,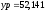 м.
м.
Решение данной задачи завершалось вычислением координат точки Р средствами Visual Basic 6.0. Был получен следующий вид решения, результат которого представлен на рис. 12.
Программный код:
PrivateSubCommand1_Click()
Cls
X1 =Val(Text1(0).Text):Y1 = Val(Text2.Text)
X2 = Val(Text6.Text): Y2 = Val(Text7.Text)
a = Val(Text3.Text) + Val(Text4.Text) / 60
b = Val(Text8.Text) + Val(Text9.Text) / 60
pi = 3.1415926
a = a * pi / 180
b = b * pi / 180
xp = (X1 * Tan(a) - X2 * Tan(b) - Y1 + Y2) / (Tan(a) - Tan(b))
yp = Y1 + (xp - X1) * Tan(a)
Print "xp="; xp, "yp="; yp
End Sub
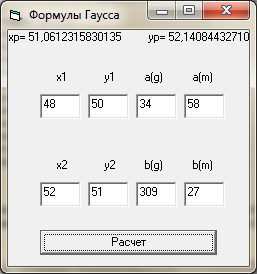
Рис. 12. Рабочее окно VisualBasicпри расчете прямой угловой засечки по формулам Гаусса.
Результат вычисления
координат точки Р
в Basic
6.0 приблизительно
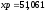 м,
м,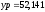 м.
м.
