Лабораторная работа 15

МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА.

Экспериментальная установка

Цель работы – измерить моменты инерции различных тел. Проверить теорему Штейнера.

Общие сведения

Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому, как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно некоторой оси ОО разобьем мысленно тело на большое число весьма малых элементов - материальных точек (рис.1). Тогда момент инерции такой отдельной элементарной массы

где - расстояние от элемента объема до оси вращения,  - плотность вещества.

Момент инерции всего тела

,

Таким образом, момент инерции различных тел можно найти с помощью интегрирования.

Рассмотрим результаты расчета для некоторых частных случаев.

1. Момент инерции материальной точки массой m , находящейся на расстоянии R от оси вращения

(1)

2. Момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр. Радиус диска R, его масса m.

(2)

.Эта же формула справедлива для момента инерции сплошного цилиндра относительно оси совпадающей с осью цилиндра..

3. Момент инерции полого цилиндра с внутренним радиусом R₁ и внешним радиусом R₂ относительно оси , совпадающей с осью цилиндра.

(3)

4. Момент инерции шара радиуса R относительно оси проходящей через его центр.

(4)

5. Момент инерции тонкого стержня относительно оси перпендикулярной к стержню и проходящей через его середину. Длина стержня l,

(5)

Эти формулы для моментов инерции относительно оси симметрии.

Момент инерции относительно произвольной оси можно найти с помощью теоремы Штейнера:

Момент инерции относительно произвольной оси О₁О₁ равен сумме момента инерции I₀, относительно оси OO, параллельной данной и проходящей через центр инерции тела и произведения массы тела на квадрат расстояния d между осями.

П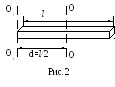олучим с помощью этой теоремы формулу момента инерции стержня относительно оси перпендикулярной к стержню и проходящей через его конец.

(6)

В общем случае расчет момента инерции представляет собой достаточно сложную задачу, и часто он определяется экспериментально с помощью основного уравнения динамики вращательного движения, методом крутильных колебаний и др.

В данной работе для экспериментального измерения моментов инерции различных тел используется метод крутильных колебаний.

Исследуемые тела насаживаются на ось спиральной пружины. Если зкрутить пружину на угол , то в результате деформации пружины возникнет упругая сила. Она создает крутящий момент (момент силы) М

M=D (7)

Здесь D – модуль кручения пружины.

Этот крутящий момент стремится вернуть пружину в исходное (равновесное) состояние. В результате возникают крутильные колебания.

Из теории крутильных колебаний следует формула для периода колебаний

(8)

где J - момент инерции.

Отсюда

(9)

Таким образом, измеряя период крутильных колебаний и зная модуль кручения D пружины, можно вычислить момент инерции тела, насаженного на ось пружины.

Порядок выполнения работы.

Для определения модуля кручения D пружины возьмите стержень с грузами и насадите его на ось пружины. Грузы сдвиньте к центру.

Поверните стержень на 90^о (/2 радиан). Прикрепите к стержню (у края грузов) динамометр и измерьте силу F. Необходимую для удержания стержня в этом положении (динамометр держите перпендикулярно стержню).

Вычислите момент силы М

М=Fl

Здесь l – плечо силы, то есть расстояние от оси вращения до места приложения силы (до места прикрепления динамометра).

	F	l	M
/2

3/2
2

Проделайте эти измерения для углов , равных 180^о, 270^о, 360^о. Полученные данные занесите в таблицу.

По полученным данным постройте график зависимости М от .

Тангенс угла наклона прямой будет численно равен модулю кручения D пружины.

Д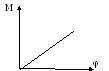алее следует измерить период колебаний системы с исследуемым телом. Для измерения периода используется устройство называемое световым барьером. Оно состоит из источника света и приемника света. На ось пружины насажена непрозрачная полоска, размещаемая между источником и приемником света. При колебаниях эта пластинка периодически перекрывает луч света. Световой барьер может работать в нескольких режимах, которые устанавливаются с помощью переключателя. Он может измерять или число колебаний, или полпериода, или целый период колебаний. Удобнее использовать режим измерения периода колебаний. Для этого переключатель устанавливают в положение, при котором на индикаторе высвечиваются четыре точки.

Процедура измерения периода следующая.

1. Насадите на ось пружины исследуемое тело.

2. Расположите всю систему так, чтобы непрозрачная полоска перекрывала луч света от источника.

3. Закрутите пружину на 180^о и отпустите.

4. После того как на индикаторе появится значение периода, запишите это значение и нажмите кнопку на световом барьере (обнулите показания индикатора).

5. Повторите измерения периода 5 – 10 раз.

6. Найдите среднее значение периода.

В данной работе можно выполнять несколько заданий.

А. Определение моментов инерции различных тел относительно оси, проходящей через центр симметрии.

1. Выберите определенное тело и насадите его на ось пружины.

2. Измерьте период колебаний системы описанным выше способом.

3. По измеренным D и T по формуле (9) вычислите экспериментальное значение момента инерции.

4. Измерьте радиус тела и определите его массу (взвесив тело).

5. По одной из формул (1 – 5) вычислите теоретическое значение момента инерции для данного тела.

Проведите измерения для различных тел (по указанию преподавателя). Можно измерять моменты инерции стержня без грузов, стержня с грузами, диска, шара, сплошного цилиндра, полого цилиндра.

В. Изучение зависимости момента инерции от расстояния масс от оси вращения.

1. Насадите на ось пружины стержень с симметрично расположенными грузами.

2. Расположите грузы на ближайшем расстоянии от оси вращения. Измерьте расстояние r от оси вращения до центров грузов.

3. Измерьте период колебаний системы.

4. Последовательно смещайте грузы на 2 см и измеряйте период.

5. По формуле (9) рассчитайте момент инерции для каждого положения грузов.

6. Составьте таблицу.

   r, (м)
   r2, (м2)
   T, (с)
   J, (кг.*м2)

7. По данным таблицы постройте график зависимости J=f(r²).

8. Теоретическую формулу для момента инерции стержня с грузами можно записать в виде

Здесь J_ст-момент инерции стержня, m –масса одного груза.

В параметрах J=f(r²) это уравнение прямой, не проходящей через начало координат. Отрезок, осекаемый экспериментальным графиком на оси ординат равен моменту инерции стержня J_ст. Сравните это значение с теоретическим значением J_ст .

Здесь m₁ –масса стержня, l – длина стержня.

С. Проверка теоремы Штейнера.

1. Насадите на ось пружины стержень без грузов. Ось пружины должна совпадать с центром стержня.

2. Измерьте период колебаний и вычислите момент инерции J_o формуле (9).

3. Сместите стержень на некоторое расстояние d от центра.

4. Измерьте период колебаний и вычислите момент инерции J .

5. Согласно теореме Штейнера

где l –длина стержня, m – масса стержня.

6. Измерьте массу стержня, его длину и расстояние d.

7. Вычислите теоретическое значение J по этой формуле и сраните его с экспериментальным значением J.