Лабараторная 4

Министерство образования РФ

Санкт-Петербургский государственный минерально-сырьевой (Горный) университет

Отчёт по лабораторной работе №4

По дисциплине: ____________Общая и техническая физика_________

^{(наименование учебной дисциплины согласно учебному плану)}

Тема: измерение скорости полета пули с помощью баллистического маятника

Выполнил: студент гр. ГНГ-12-2 /Сляднева Д.А./

^{(подпись) (Ф.И.О.)}

Принял: /Ремзова Е.В./

^{(подпись) (Ф.И.О.)}

Санкт-Петербург

2012 год.

Цель работы – определить скорость полета пули с помощью крутильных колебаний баллистического маятника.

Краткое теоретическое обоснование.

Явления, изучаемые в работе: явление неупругого соударения тел, в результате которого баллистический маятник совершает крутильные колебания.

Основные законы и соотношения, на основе которых получены основные расчетные формулы:

При выводе расчётных формул использованы формулы для момента инерции и периода крутильных колебаний физического маятника, а также законы сохранения момента импульса и полной механической энергии. Принято допущение при этом о малости неконсервативных сил.

На основании закона сохранения момента импульса можно написать

,   (1)

где m - масса пули;  - величина скорости пули; l - расстояние от оси вращения маятника до точки удара пули;  - величина угловой скорости маятника; J - момент инерции маятника.

Согласно закону сохранения полной механической энергии при повороте маятника кинетическая энергия маятника переходит в потенциальную энергию закручивающейся проволоки

, (2)

где - наибольший угол поворота маятника; D - модуль кручения проволоки.

Учитывая, что момент инерции пули существенно меньше момента инерции маятника J , из уравнений (1) и (2) получим                              

.    (3)

Модуль кручения проволоки D можно определить, измерив период крутильных колебаний маятника Т.

При малых углах отклонения период крутильных колебаний маятника определяется по формуле

(4)

Модуль кручения проволоки

(5)

Подставив выражение (5) в уравнение (3), выразим величину скорости пули

= (6)

Чтобы исключить измерения момента инерции J, запишем периоды колебаний маятника Т₁ и Т₂ при различных положениях грузов R₁ и R₂:

  (7)

отсюда

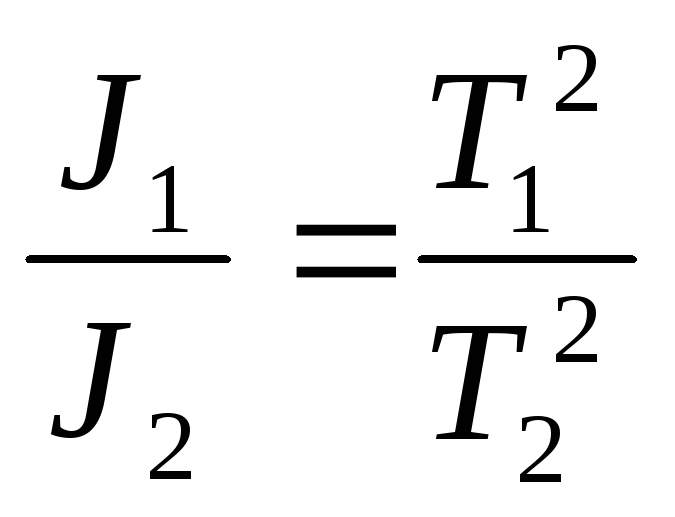(8)

В силу того, что момент инерции величина аддитивная, момент инерции баллистического маятника с грузами выразим в виде суммы

(9)

где М - масса двух неподвижных грузов; R - расстояние от центра масс груза до оси вращения; J₀ - момент инерции маятника без грузов.

Для различных положений грузов на расстояниях R₁ и R₂:

в первом положении ; во втором положении

Разность моментов инерции

(10)

Решая уравнение (8) и (10) относительно J₁ найдем

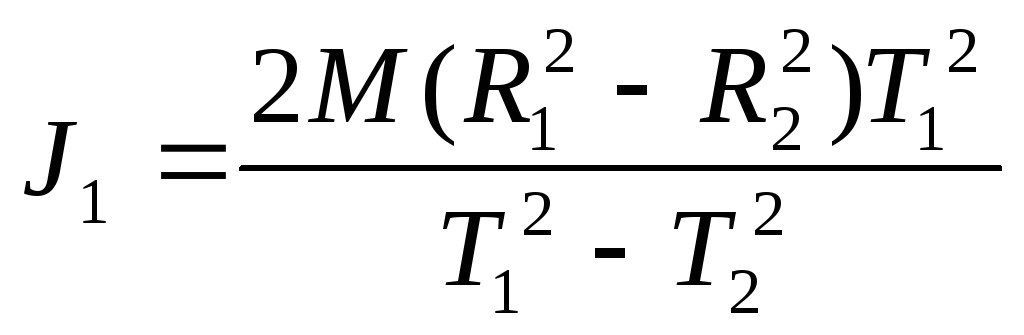  (11)

Подставив в формулу (6) период T₁ и момент инерции J₁ для положения грузов на расстоянии R₁, получим окончательную формулу для расчета величины скорости пули

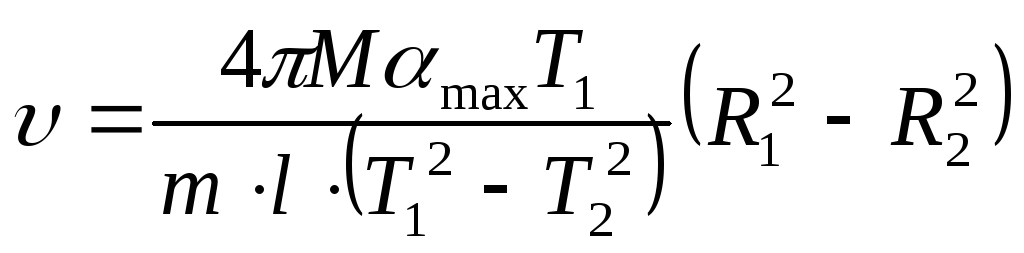. (12)

Схема установки:

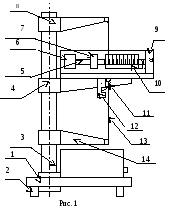
1. Основание

2. Регулирующие ножки

3. Колонка

4. Средний кронштейн

5. Стержни

6. Мисочки

7. Вращаемые грузы

8. Верхний кронштейн

9. Стреляющее устройство

10. Угловая шкала

11. «Водилка»

12. Фотоэлектрический датчик

13. Проволока

14. Нижний кронштейн

Основные расчетные формулы.

1. Момент инерции тела

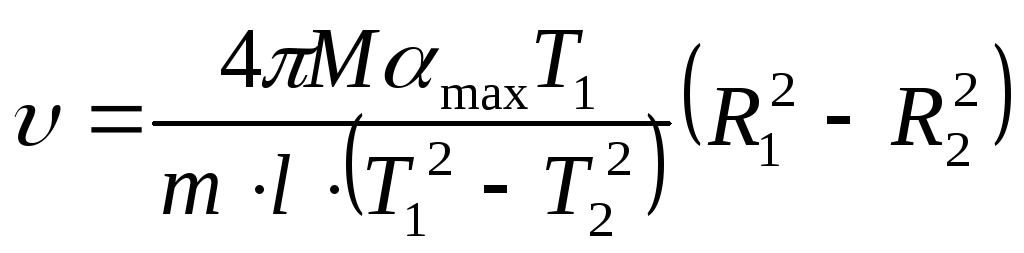
m – масса пули [кг]

М - масса груза [м]

Т₁ и Т₂ – периоды колебаний маятника при различных положениях грузов R₁ и R₂[с]

– наибольший угол поворота маятника,[рад]

– расстояние от оси вращения маятника до точки удара пули, [м]

2. Период колебания

T = t/10.

Погрешности прямых измерений.

t = 0.001 c

R = 0.0005 м

= 0.0005 м

m = 0.001кг

M = 0.1кг

= 0.5⁰

Погрешности косвенных измерений.

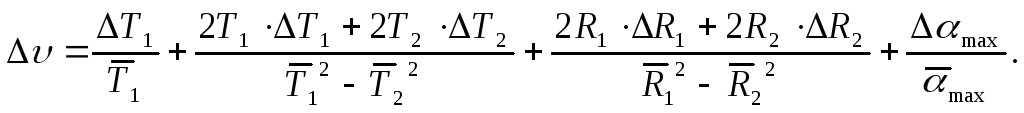
Таблицы для занесения результатов измерений.

Таблица 1

Величины	r1	t1		t1	r2	t2	t2			m	mпул
	м	с		с	м	с	с	м/с	м	кг	кг	град.
1	0.0905	22,323	2,2323		0,021	12,889	1,2889	9,354989	0,115	3,648 *10-3	0,2	17
2		22,331	2,2331			12,885	1,2885	9,345143
3		22,329	2,2329			12,883	1,2883	9,345355
4		22,333	2,2333			12,884	1,2884	9,342725
5		22,332	2,2332			12,882	1,2882	9,342131

Расчет результатов эксперимента

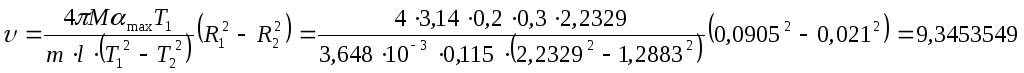
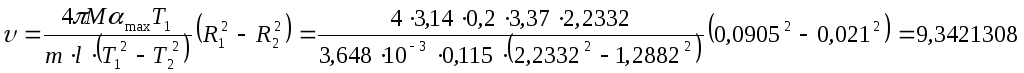
Средняя квадратичная погрешность

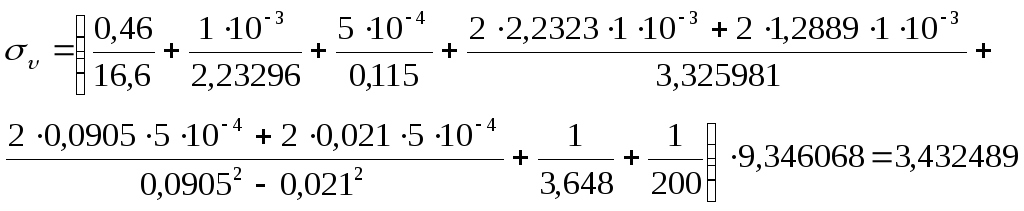
Окончательные результаты.

Вывод.

В ходе лабораторной работы была определена скорость полета пули с помощью баллистического маятника. Найденное среднее значение скорости пули имеет значение . Вычислив погрешность измерения, мы получили, что она равна и является достаточно большой относительно найденной скорости. Для более большой точности измерения требуется применение специальной аппаратуры.