6. Определенный интегрл,приложение. Несобственный интеграл.

6.1 Интегральная сумма. Определенный интеграл.

Рисс.1) На отрез [а,в]задана неприр. ф-я Разобьем отрез. [а,в]произвольным образом на n частей:

а=х_о; х₁,х₂,…….х_n-1,х_n, при этом х_o<х₁<х₂<…<х_n

Обозначим ∆х₁=х₁-х₀; ∆х₂=х₂-х₁

,….., ∆xn=xn-xn-1 –длины типичных отрезков

На каждом из частичн. отр. [xi-1;xi], где i=1,2,….,n

Произвольным образом выбираем точку Сi

В каждой из этих точек вычислим значение ф-ии f(c1),f(c2)….,f(cn) и составим сумму :

??n=f(c1)* ∆x1+f(c2)* ∆x0+…..+f(cn)* ∆xn (6.1.1)

Опред.: эта сумма назыв. Интегральной суммой для ф-ии f(x) yf jnh [a;b]

Гео метрический смысл интегральной суммы

Интегр.сумма зависит от способа разбиения отр. [a;b] на частичные отрезки [xi-1;xi] и выбора опорных точек Сi внутри частичных отрезков.

Обозначим наибольшую из длин отрезков при данном разбиение.

Рассмотрим некоторые последов разбиений, при котор((((( ))))и при этом n→∞

Опред.: если при любых разбиениях отрезка [a;b] : (((((()))))) и при любом выборе точке Сi интегральная сумма 6.1.1 стремиться к одному и тому же пределу S:

То этот предел назыв. определ. интегралом от ф-ии f(x) на отр [a;b] и обозначается

Числа a и b соответств. назыв. нижним и верхним пределами интегрирования

Отрезок [a;b] называв.отрезком интегрирования; х-переменная интегриров-я

По определению:

(6.1.2)

Опред.: если предел для 6.1.2 существ, то ф-ю называют ИНТЕГРИРУЕМОЙ на отрезке [a;b]

Геометрич-ки опред. Интеграл

От ф-ии f(x) при a<b и f(x)>=0 равен площади криволинейной трапеции ограниченной графиком ф-ии y=f(x), осью OX и прямыми х=а и х=b

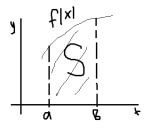
Пример:

ТЕОРЕМА СУЩЕСТВОВАНИЯ

Т.1 если ф-я y=f(x) непрерывна на отр. [a;b] то она интегрируема на этих отрезках

Y=f(x)€C[a;b] => &&&

Т.2 если ф-я y=f(x) ограничена на отр [a;b] и непрерывна на этом отрез. Всюду за искл. Конечного числа точки разрыва, то она интегрир. на этом отрезке.

Привер: ф-я Дирихле

Ф-я на отр [0;1] неинтегрируема

6.2 Свойства определен. Интегр.

1. a=b =>

2. a<b ???? => ???? и

3. Свойство аддитвности

=>

4. =>

5. определ. интеграл от алгебраич суммы нескольких ф-й равен алгебраич .сумме интеграл-ов от слагаемых

=>

Свойства 4 и 5 назыв. Линейными свойствами опред интеграла

6. f(x)>=0 =>

7. если выполняется f(x)<=g(x), f(x) и g(x) =>

Свойство монотонности

8. если m и M наименьш. И наиб. Знач ф-ии f(x) на отр [a,b], где a<=b и => справедливо равенство:

Доказательство:

=>(по свойст 7)==>

(по свойст 4)=>

Геометрический смысл доказанных неравенств.

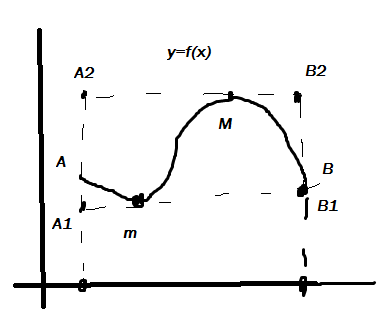
Если f(x)>=0,то S кривол.трак. то S_aA1B1b =<S_aABb=<S_AA2B2b

9. если существует интеграл и выполнятся неравенство:

Модуль интеграла не превосходит интеграла модуля Док-во: справедливо соотношение

если а) f(x)>0 б)f(x)<0 по свойст. 7 получим:

=>(  ) =>

=>

10. если сущ.интегр. (проверь так ли, у оли не понятно), и для всех х[a,b],, k-const , a<b и

Это сво-во следует из сво-ва 9 с учетом сво-ва 4 и 7 .

11. Т.о среднем

Если ф-ия y=f(x) непрерывна на отр. [a,b] тогда на этом отрезке найдется точка С: выполняется равенство:

Док-во:

Из св-ва 8 => m(b-a) => m=>

причем

по усл. f(x) неприрыв. ф-ия и обязательно принимает хотя бы 1 раз значение зключительное между m и M => C [a,b] , => (((((((()))))))))

=> - формула среднего значения а f(c)-среднее знач. Ф-ии на отр. [a,b]

Геометрич. Смысл:

Площадь ограниченная криволин-й трапецией, осью ОХ, прямыми х=а, х=b площадь равнове???????? Площади прямоугольн. Высотой f(c) и основанием длиной (b-a)

12. Определенный интеграл зависит только от подъинтегральной функции f(x) и отрезка интегрирования [a;b] и не зависит от переменной интегрирования, которую можно обозначать любой буквой.

Определенный интеграл по симметричному отрезку.

13. Если f(x) – четная функция

f(-x)=f(x) из этого следует что

14. Если f(x) – нечетная функция

f(-x)=-f(x) из этого следует что

Свойства 13, 14 будут доказаны, когда будет «замена переменной в определенном интеграле».

6.3 Производная от интеграла по его верхнему пределу.

Теорема Барроу.

Пусть в определенном интеграле нижний предел постоянный, а верхний изменяется, тогда будет изменяться значение интеграла, т.е. при рассмотренном условии интеграл есть функция своего верхнего предела.

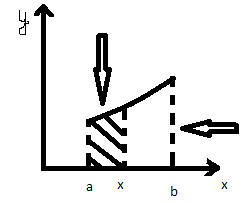
При постоянной а, этот интеграл будет собой представлять функцию верхнего предела

Теорема Барроу: Если f(x) – непрерывная функция на [a;b] и - функция верхнего предела, то тогда _{от x} {производная от функции верхнего предела равна подынтегральной функции}.

Доказательство: Пусть -приращение аргумента ,тогда приращение функции Ф(х) будет равно:

{по условию}={для первого слагаемого в алгебраической сумме применим св-во 3}={св-во 11(т. О среднем)}=

{с учетом }= {по условию f(x) – непрерывная функция}.

Из теоремы Барроу следует что

6.4 Формула Ньютона – Лейбница

Теорема: Если

Если F(х) – есть какая-либо первообразная от функции f(х), которая непрерывна на [a,b], тогда справедлива формула Н.-Л.

Доказательство: Пусть F(x) – некоторая первообразная от функции f(x), то по теореме Барроу

Две любые первообразные от данной функции отличаются на постоянное слагаемое – С.

Воспользуемся {знак двойной подстановки}

По св-ву 12 () и получим формулу Н. – Л.

Вывод: формула Н.- Л. позволяет вычислить определенный интеграл в том случае, когда известна первообразная подынтегральной функции.

Примеры:

1)

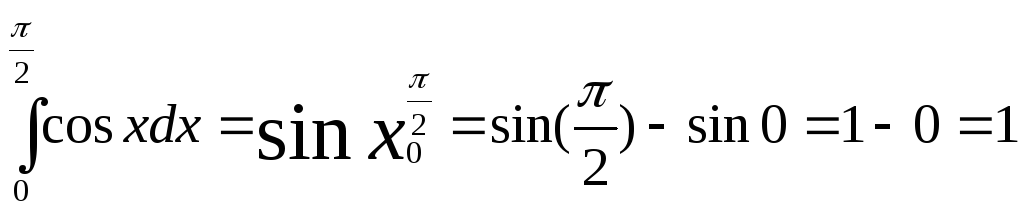
2)Вычислить среднее значение функции: f(x)=x на отрезке [0,n/2]

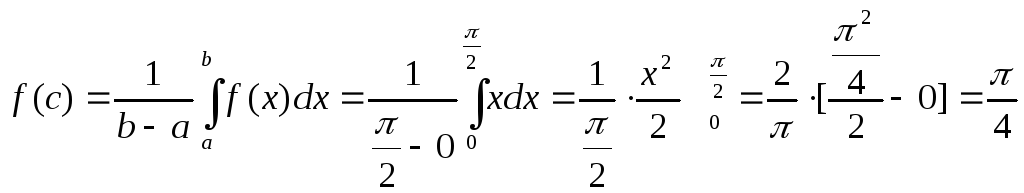
6.5 Замена переменной в определенном интеграле

Пусть функция y=f(x) определена и непрерывна на отрезке [a,b], t - новая переменная, такая что x=g(t).

Пусть функция g(t) – непрерывна на отрезке [], имеет

1) - непрерывную производную на этом отрезке.

2)

3)тогда справедлива формула замены переменой в определенном интеграле.

6.5.1

Доказательство: Пусть F(x) первообразная для f(x) по определению первообр.

Интегрируя оба равенства в пределах от a до b получаем

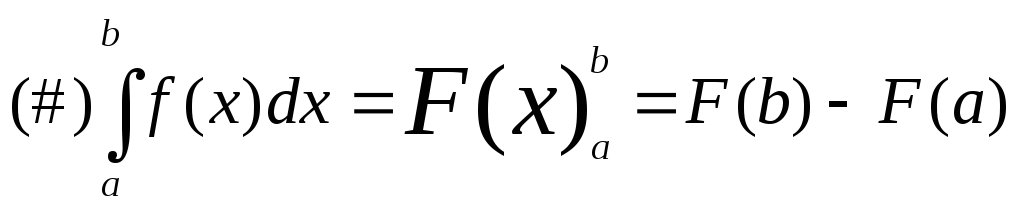по формуле Н. – Л.

По условию 2 теоремы: Правые части последующих выражений равны, то равны и левые—что и доп. формулу замены переменной в определенном интеграле.

Замечание: при вычислении определенного интеграла по 6.5.1 к старой переменной не возвращаемся.

Примеры:

1)

=

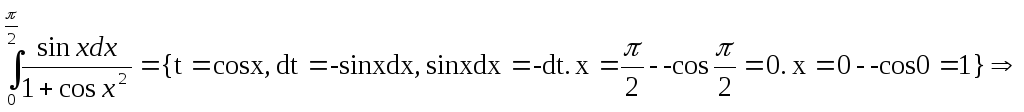
2) Формула дл интеграла по симметричному отрезку от -а до а

=

четная функция

нечетная функция

3)

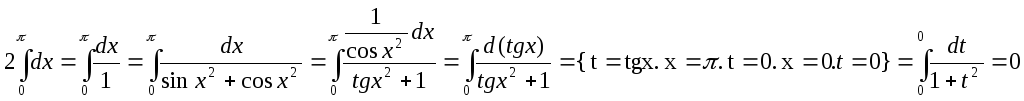
6.6 Интегрирование по частям в определенном интеграле.

Пусть U(x), V(x)

Докажем формулу интегрирования по частям в определенном интеграле

- формула интегрирования по частям.

Пример:

=

6.7 Несобственные интегралы

В определенном интеграле

1)[a,b]

2)

Возникает необходимость распространить определенный интеграл на случай:

1)бесконечного промежутка интегрирования

2)разрывной подынтегральной функции

Признаки сходимости несобст-ых Интег-ов с бесконечн. Предел.

Т.1 Если для x

;

Т.2 Для случая ф-ии х выполняется неравенство 0 и

-расходятся.

Т.3 для случая ф-ия f(x) имеющий знак в бесконечном промежутке,

Если dx , этот абсолютно сходящийся .

6.7.2 от неограниченных ф-ий. Несобственный 2-го рода.

Сущ-ет у=f(x) определена и непрерывна для всех х принадлежащих на [a,b) в (.) х=b либо определена, либо имеет бесконечный разрыв.

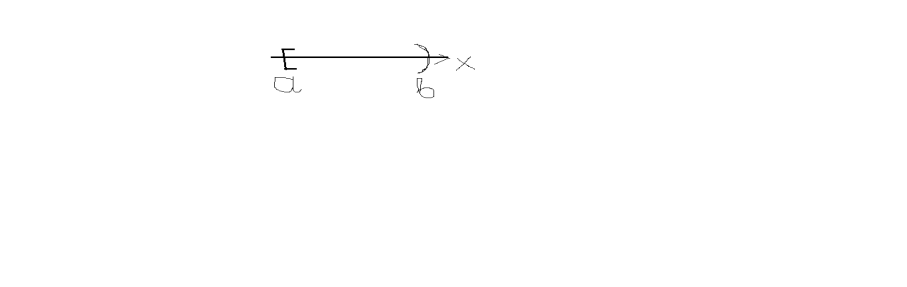
Определение ф-ии f(x) в (.) по определению равен:

(6.7.2.1)

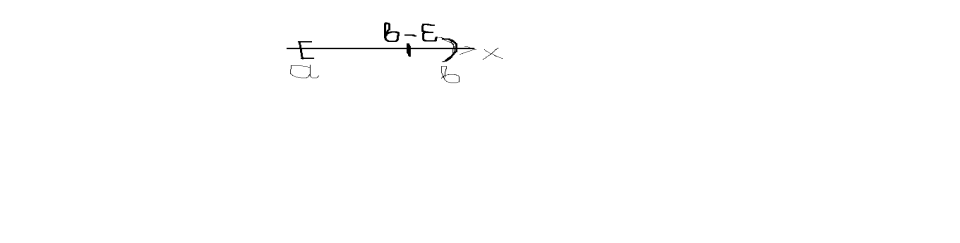
Если предел в правой части сущ-ет и конечен, то несобственный наз-ся Сходящимся, в противном случае (предел не сущ-ет или = , наз-ся Расходящимся.

Пусть ф-ия у=f(х) не прерывна на [a,b] в (.) х=с ф-ия или неопределенно либо имеет бесконечн разрыв , то по определению , , то ,

(6.7.2.2)

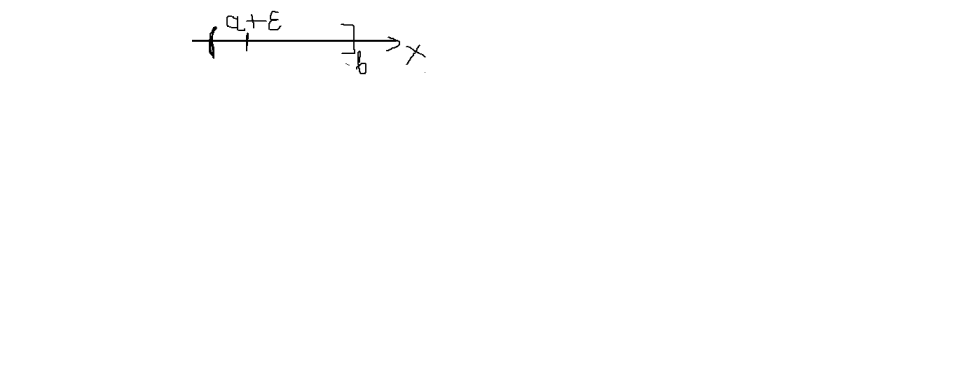
Если предел в правой части сущ-ет и конечен , то Интег-ал назыв-ся Сходящимся, в противном случае Расходящимся!

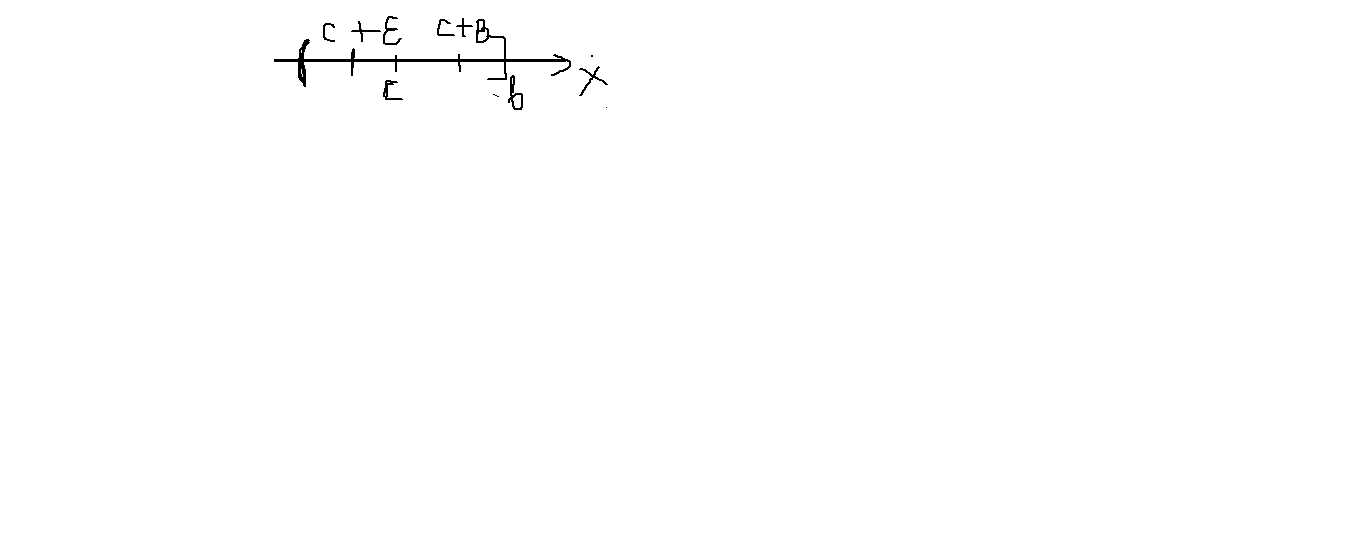
Если ф-ия у=f(x) имеет бесконечный разрыв в (.) х=с или неопределена, где асb , тогда

(6.7.2.30)

Если сходится одновременно оба Интег-ла в Прав. Части , то сходится Интег-л и в левой части. Если хотя бы один из Интег-лов в Прав-й части расходится, то расходится и Интег-л в левой части.

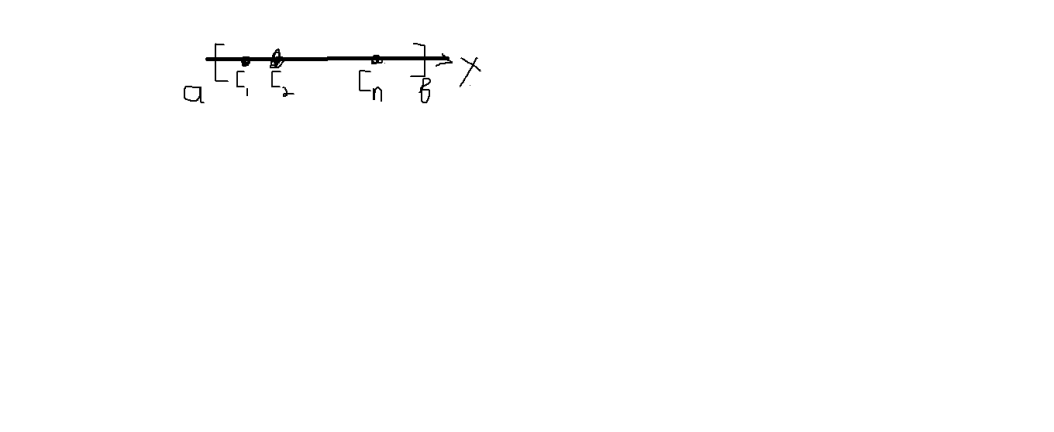
Если функция у=f(x) на отрезке [a,b], где она определена и непрерывна, и имеет конечное число (.) разрыва тогда несобственный Интеграл определяется следующим образом:

Если каждый из несобственных в правой части равенства сходится, то сходятся в левой части, если хотя бы один из них расходится, то расходится и исходный .

Признаки сходимости несобственных от разрывных фун-ий.

Т.1 Если на промежутке [a,b) ф-я у=f(x) и g(x) определены и непрерывны в (.) x=b эти ф=ии имеют разрыв для всех ,

Из геометрич. смысла определённого интеграла для областей задаваемых соотношениями a x b, y₁(x)yy₂(x) справедлива формула для вычисления S области , ограниченной графиками ф-ий y₁(x), y₂(x) и прямыми x=a, x=b.

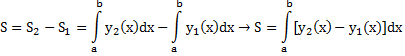
Е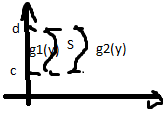сли область задана с соотношениями cyd , g₁(y)x g₂(y), то

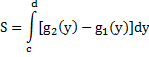
Если прямая линия задана параметрически ,x(t), y(t) , непрерывн. диф. на отрезке . x(=a; x()=b