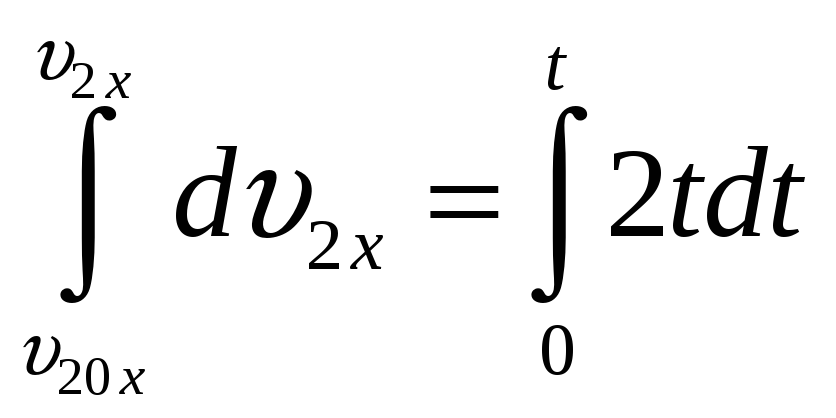Расчетно-графическая работа 1.

Кинематика поступательного движения

Вариант 1.1.14

Формулировка задания

По одной прямой, совпадающей с осью Ox декартовой системы координат, движутся две материальные точки.

Координата при движении первой точки изменяется по закону , а проекция ускорения второй точки изменяется согласно уравнению . В начальный момент времени вторая точка имела координату и скорость .

Размерности коэффициентов:

[A] = м, [B] = м/с, [C] = м/с², [D] = м/с³,

[ ] = м/с² , [ ] = м/с³, [ ] = м, [ ] = м/с.

Определите скорость первой точки в момент времени, когда вторая остановится.

Значения параметров:

				A	B	C	D
0	2	5	-4	5	2	-2	1

Теоретические основы работы:

В данной расчетно-графической работе рассматривается кинематика поступательного движения материальной точки.

Материальная точка – это тело, размеры которого пренебрежимо малы по сравнению с масштабами движения.

Механическим движением тела (материальной точки) называется изменение его положения в пространстве с течением времени относительно других тел.

Поступательное движение – это одна из разновидностей механического движения, при котором любая прямая, жестко связанная с телом, остается при его движении параллельной своему первоначальному положению. При этом все точки прямой имеют одинаковые скорости и ускорения.

У каждой движущейся материальной точки есть траектория – линия, образованная совокупностью последовательных положений в пространстве, занимаемых точкой в процессе ее движения. В данной расчетно-графической работе рассматривается прямолинейное движение, траекторией которого является прямая линия.

По характеру изменения скорости и ускорения движение может быть равномерным и неравномерным (равнопеременным и переменным). В свою очередь, равнопеременное движение может быть равноускоренным и равнозамедленным.

Пространственное положение и движение материальной точки можно задать с помощью декартовой системы координат.

Кинематическое уравнение движения материальной точки

(1)

Представление радиус-вектора в декартовой системе координат

(2)

где – единичные векторы вдоль координатных осей x, y, z

Вектор перемещения

(3)

Вектор мгновенной скорости

(4)

Модуль мгновенной скорости

(5)

Путь, пройденный материальной точкой

(6)

Вектор и модуль скорости в декартовой системе координат

, (7)

Проекции скорости

, , , (8)

Вектор мгновенного ускорения

или (9)

Проекции ускорения, выраженные через проекции скорости

, , , (10)

Проекции ускорения, выраженные через координаты (проекции радиус-вектора)

, , , (11)

Вектор и модуль ускорения в декартовой системе координат

, (12)

Средняя скорость перемещения

(13)

Модуль средней путевой скорости

(14)

где - путь, пройденный за время

Решение задачи:

Дано: A = 5 м B = 2 м/с C = -2 м/с D = 1 м/с3  = 0 м/с2  = 2 м/с3  = 5 м  = -4 м/с Найти: в момент, когда

Решение: По условию уравнение координаты первой точки . Подставим в него значения параметров A, B, C, D. Получим уравнение . Также подставим значения параметров  и  в уравнение для ускорения второй точки . Получим . Для того чтобы определить скорость первой точки в момент, когда вторая остановится (), необходимо найти уравнения, задающие данные скорости. Найдем уравнение скорости первой точки . По определению (4) Но так как точка движется вдоль Ox, то уравнение примет вид: (15) (16) Найдем уравнение скорости второй точки . По определению (9) вектор мгновенного ускорения определяется как Но так как точка также движется вдоль оси Ox, то уравнение примет вид: (17) Выразим : (18) Чтобы найти , проинтегрируем обе части выражения, предварительно подставив. Но так как по условию , то (19) Из п. 3 и п. 4 получили, что , Найдем, при каком t , для этого решим квадратное уравнение Но время не может быть отрицательным, поэтому Проверка размерности , , , . Вычисление при ():

Ответ: в момент времени, когда вторая точка остановилась (,), первая точка имела скорость равную 6 м/с.

5